

(Takes a little while loading the images)
e-mail :

This document (Part XXIX Sequel-31) further elaborates on, and prepares for, the analogy between crystals and organisms.
Conclusion of the Philosophical Context (VIII) of the Crystal Analogy, and Resumption of its Morphological Context.
In order to find the analogies that obtain between the Inorganic and the Organic (as such forming a generalized crystal analogy), it is necessary to analyse those general categories that will play a major role in the distinction between the Inorganic and the Organic : Process, Causality, Simultaneous Interdependency and the general natural Dynamical Law. This was done in earlier documents.
Sequel to the Categorical Analysis of 'Dynamical System ' and of Causality in terms of thermodynamics.
In previous documents we studied the general nature of systems that either are :
Causality
As in close-to-equilibrium dynamical systems (such as in thermodiffusion), the applied fall (that is, some applied difference) in far-from-equilibrium systems (for instance a temperature difference, as we have it in the Bénard instability) ultimately is the result of leveling-out processes elsewhere. And thus, like in equilibrium systems, the causal action of all non-equilibrium systems (linear as well as non-linear) can be reduced to leveling out. And regarding the tendency toward leveling out we have already established that causality intrinsically contains a probabilistic aspect. So also for far-from-equilibrium systems this characterization of causality holds. In fact, when we consider a non-equilibrium system (linear or nonlinear), we must conceptually shift the boundaries of such a system as to include the remote leveling-out processes that are ultimately responsible for the fall (for instance, difference of temperature) of non-equilibrium systems.
What remains to be incorporated (or not to be incorporated, as it could turn out) into the content of the category of Causality is the conjectured holistic aspect of crystals as well as of dissipative structures (i.e. the products of far-from-equilibrium dynamical systems, such as the structure that emerges in the Bénard instability). This aspect cannot, for the time being, be further analysed.
The thermodynamic status of Branched Crystals (dendritic crystals).
We hope to determine the thermodynamic status (equilibrium structures, close-to-equilibrium structures, far-from-equilibrium structures [dissipative structures] ) of branched crystals, by investigating them thermodynamically and comparing their general features with those of the Bénard instability.
The branched crystal, because of its high morphological potential, will play a prominent role in the crystal analogy. And because we are only out for generalities, it is sufficient to study one single substance in this respect. And the best one to choose is certainly the substance H2O, water. For this substance there already always has been a giant laboratory in which experiments with changing temperatures, pressures and humidities were carried out on water, -- the atmosphere. We have seen the many diverse snow crystals and ice feathers, showing the full morphological potential as it is already present within a relative narrow range of temperature and pressure. So we will concentrate on the genesis of branched structures as we see them in snow crystals and in windowpane frost, and we will try to assess their thermodynamic status.
For this we will first study the relevant phase transitions of H2O, which are here the transitions from water vapor to ice, and from ice to water vapor (Recall that snow crystals are not formed by the freezing of liquid water, but by the solidification directly from water vapor. Further, I think it highly probable that also the ice feathers of windowpane frost come directly from water vapor). Of course, we will make use of results obtained in earlier documents.
Secondly we will study the special case of branching as we see it in all dendritic H2O crystals of snow and windowpane frost. When the crystal is forced to grow rapidly (strong undercooling, high humidity), only the directions of intrinsically most rapid growth will be supplied with material, because they can take up the most material per unit time, and so we see branches appear in the directions of intrinsically most rapid growth. These directions are the directions to which the corners of the ice hexagon point (giving the six main branches) and, of course, all directions parallel to them (giving the side branches). In slowly grown ice crystals the faces, corresponding to these directions of fast growth, have grown themselves out of existence. In addition to this, the corners of an incipient ice hexagon stick out, so they are best surrounded by water vapor, and thus best supplied with it, so they will be privileged when crystallization is forced to proceed rapidly. Moreover, the corners reach into higher supersaturation levels of the diffusion field around the crystal, causing these corners to grow faster.
Also here we will make use of results obtained in earlier documents.
Supersaturation, Vapor pressure, Vapor density.
Before we (continue to) study dendritic crystallization from a thermodynamic viewpoint (instead of from a morphological viewpoint as was done in earlier documents), we must first settle things that relate to the concepts of (water vapor) supersaturation, (water) vapor pressure, and (water) vapor density, which play a dominant part in the formation of ice crystals in or from the air.
We make use of the writings of several authors :
Vapor pressure has been discussed earlier, namely in Part XXIX Sequel-13 . Let us reproduce the phase diagram of Water (as it was depicted there) and recall where (equilibrium) vapor pressure comes in :
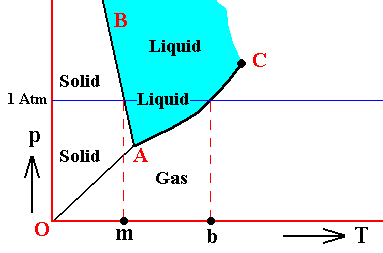
Figure above : (Approximate) Phase diagram of H2O (water) as a one-component system (C = 1). The phases are Ice, Water and Water vapor. A = triple point, AB = melting curve, AC = vapor-pressure curve of liquid water, OA = vapor pressure curve of solid water (ice), C = critical point, m = melting point (2730K = 00C) at 1 Atm, b = boiling point (3730K = 1000C) at 1 Atm.
The phase diagram of water is subtly different from that of most other substances. The solid-liquid boundary slopes NNW, not NNE. This is a direct consequence of the fact that water has the unusual property of getting less dense when it freezes. The triple-point pressure of H2O is 4.6 mm mercury, and its triple-point temperature is 0.0070C (See also BALL, Ph., H2O, a Biography of Water, 1999, 2000, p.150).
The (equilibrium) vapor pressure of a liquid is the pressure of its corresponding gas while the latter is in equilibrium with the liquid phase.
If we have a particular gas A, which could be a component of a mixture of gases, (a gas A) that has a pressure higher than the equilibrium vapor pressure of the corresponding liquid, at a given temperature, then it is as such unstable. The gas mixture is supersaturated with that particular gas A with respect to the liquid. Generally, when suitable condensation nuclei are present, part of the gas will condense to liquid (which takes a much smaller volume than the corresponding amount of gas) lowering its pressure (which is a partial pressure of the overall pressure) until the equilibrium vapor pressure of the corresponding liquid has been reached. Then, on average, as many particles leave the liquid as return to it. The mixture is saturated with gas A.
When, on the other hand, the gas A happens to have a lower pressure -- as partial pressure of the overall pressure of a mixture -- than the equilibrium vapor pressure of the corresponding liquid at a given temperature, this liquid, when present, will continue to evaporate. The mixture is undersaturated with respect to gas A. While the pressure of gas A is in this case lower than the equilibrium vapor pressure of the corresponding liquid, it could still be higher than the equilibrium vapor pressure of the corresponding solid at some lower temperature. See next diagram, which takes water as an example.
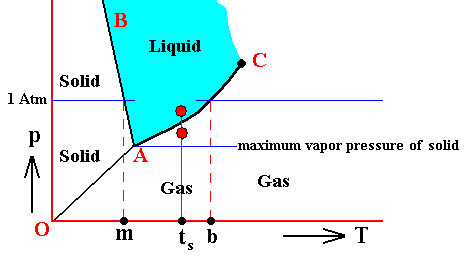
Condensation, that is the transition of a vapor into the corresponding liquid phase, and evaporation, that is a transition of a liquid into its corresponding vapor phase, might need some additional explanation :
For the substance H2O, water, we can predict under what conditions what phase will emerge from its vapor, if we assume that condensation- or freezing-nuclei are present :
If we have water vapor that is :
If, on the other hand, we have water vapor that is :
If, further, we have water vapor that is :
If, finally, we have water vapor that is :
All this can be illustrated by considering the phase diagram of water (taken from the website of Kenneth LIBBRECHT ) :
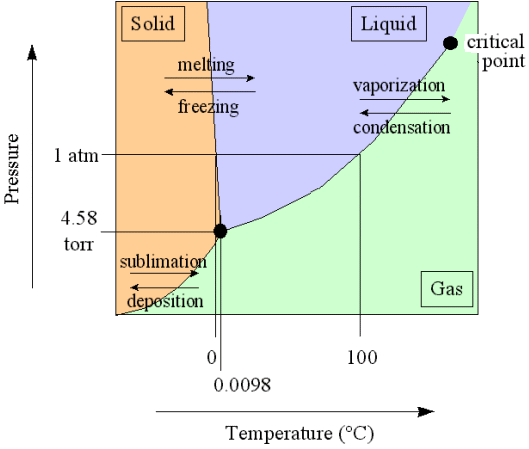
Let us continue with the formation of snow crystals in the atmosphere.
Click HERE to see the Nakaya morphology diagram, or inspect an enlargement of it :
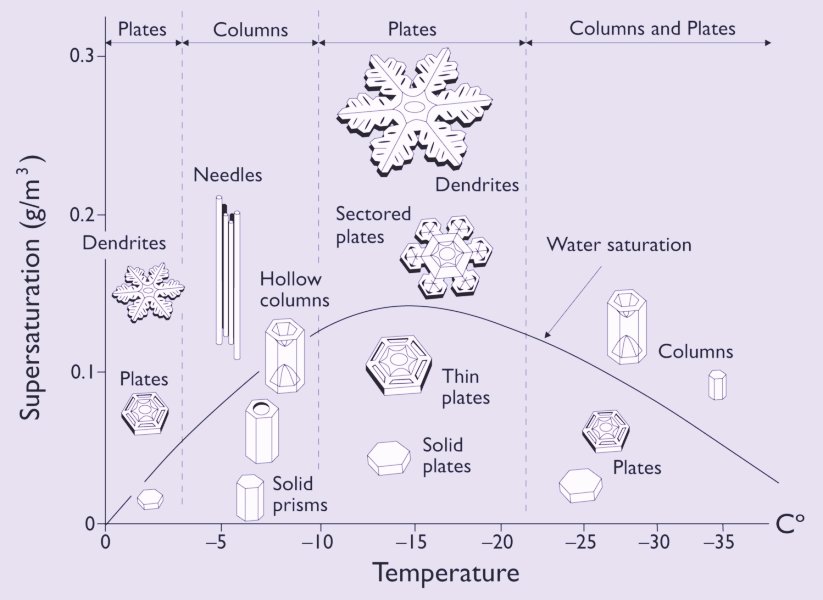
The vertical axis of this diagram displays (if I have things well understood) the excess vapor density with respect to ice (density = weight / volume). This translates into supersaturation with respect to ice as follows ( FURUKAWA, Fig.2) (where we represent the "with respect to . . ." by a subscript) :
supersaturation ice = (excess vapor density ice ) / (equilibrium vapor density ice )
The excess vapor density ice is -- expressed as partial pressure (LIBBRECHT, website, Physical Properties of Ice) :
P water - P ice ,
that is (according to me), the actual pressure of water vapor (not the equilibrium vapor pressure, but the pressure as it could turn out in some measurement) minus the equilibrium water-vapor pressure of ice.
The supersaturation ice is according to LIBBRECHT :
( P water - P ice ) / P ice .
The curve in the Nakaya morphology diagram is the saturation line with respect to liquid water.
Above this curve the air is supersaturated with respect to liquid water (and in any case, with respect to ice).
Below the curve the air is undersaturated with respect to liquid water, but still supersaturated with respect to ice, that is, the pressure of the water vapor is still higher than the equilibrium water-vapor pressure of ice.
This latter can (also) be seen in the next diagram given in LIBBRECHT 's website (with logarithmic scale) : There we see the equilibrium water-vapor pressure curve (as a function of temperature) for liquid water at and above 00 C, and also for undercooled water (liquid water with a below-zero temperature). We can see this diagram HERE
or can inspect an enlargement of it :
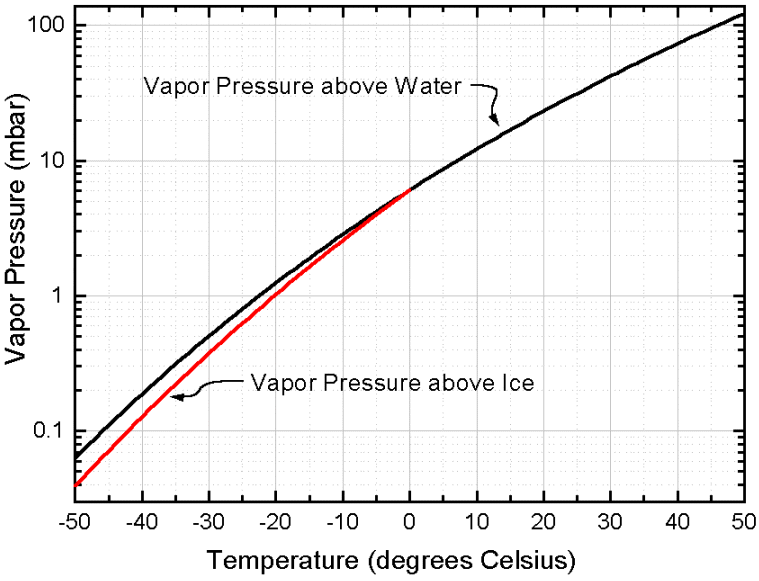
The equilibrium water-vapor pressure curve (also as a function of temperature) for ice (red) only extends till 00C, because superheated ice cannot exist (in contrast to undercooled water). This equilibrium water-vapor curve for ice runs below the equilibrium water vapor curve for liquid (undercooled) water, which indeed means that we can have undersaturation with respect to liquid while still supersaturation with respect to solid.
The diagram just depicted, thus displays the equilibrium water-vapor pressure of liquid water (black curve) over the temperature range -500 C --- 500 C, and the equilibrium water-vapor pressure of ice (red curve) over the temperature range -500 C --- 00 C.
These curves should be interpreted as follows :
If we have, at a given temperature, a closed vessel containing some liquid water and air + water-vapor, and if the whole system is in equilibrium (that is, as many water molecules [how much an amount of water molecules this may be, depends on the temperature] leave the liquid as return to it), then we can measure the equilibrium water-vapor pressure of liquid water belonging to that given temperature. See next two Figures.
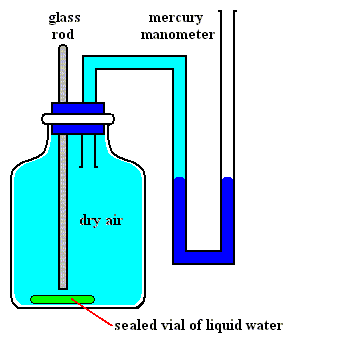
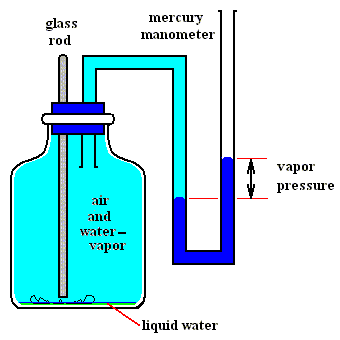
Figures above : Determination of the vapor pressure of liquid water.
Upper Figure : A vessel containing dry air, and a manometer.
Lower Figure : Measurement of vapor pressure of water.
A sealed small vial containing liquid water is broken (lower Figure) by pushing down a glass rod. Part of the released liquid water evaporates. A little bit liquid water remains at the bottom of the vessel. The change in pressure as we see it when comparing the situation before and after the liberation of liquid water is equal to the equilibrium water-vapor pressure of liquid water at the temperature at which the experiment was carried out.
(After OUELLETTE, R., Introductory Chemistry, 1970, Figure 3.3, p.66)
As one can see, the total pressure has become a little bit higher than it was before the liquid water was released, that is, it is now a little bit higher than atmospheric pressure. The excess is equal to the equilibrium water-vapor pressure of liquid water at the temperature of the experiment.
Now the curve in the Nakaya Morphology Diagram is the water saturation line, so this curve must represent equilibrium situations, that is, equilibria between the amount of water molecules leaving the liquid phase (here represented by water droplets in the air) and the amount of water molecules entering it. But now we don't have to do with a closed vessel anymore, but with the open air, that is, an open 'vessel'. So this curve does not measure the equilibrium water-vapor pressures of liquid water for the given temperature range (00C --- -350C), but just the points where the atmosphere is saturated with water vapor with respect to liquid water. And this is why this curve is not identical with the corresponding part of the curve (black line) in the above diagram of LIBBRECHT , that is, the part referring to undercooled water (in the air). A second reason for the large discrepancy between the two curves could be the fact that a horizontal (that is, not curved) surface of (remaining) water, as it is the case in the closed-vessel experiment, results in a lower escaping tendency (for molecules to leave the liquid phase) than we see it in a strongly curved surface of remaining water -- a given particle at such a surface has a smaller number of close-neighboring particles that attract it to prevent it from escaping -- as it is the case for (undercooled) water droplets floating in the air, and as it can be expected in more or less dense clouds. And it is these clouds to which the water-saturation curve in the Nakaya diagram refers. Let's elaborate on this a little further.
Decrease of temperature tends to lower the saturation pressure ps of water vapor in the air, that is the 'equilibrium' water-vapor pressure (as it is present) above liquid water.
On the other hand, decrease of the size of water droplets (that is increase of the curvature of the water surface) tends to increase the escaping tendency and thus the 'equilibrium' water-vapor pressure above liquid water (droplets).
Now, it could be, that the size of the water droplets in the air decreases when the temperature goes from 00C to round about -150C (and thus having the radius of curvature of the water surface decreased), and so entailing a tendency to increase the 'equilibrium' water-vapor pressure. We could further assume that this more than compensates for the tendency of decreasing the 'equilibrium' water-vapor pressure (this latter tendency) as a result of the temperature decrease ( 00C ==> -150C ).
After about -150C, that is, when the temperature decreases still further, we could assume that this latter decrease gains the upperhand in decreasing the 'equilibrium' water-vapor pressure ( ps ) above liquid water.
All this might explain the shape of the water-saturation line as we see it in the Nakaya Morphology Diagram. But of course in this consideration the decrease of water-droplet size along the temperature course 00C ==> -150C is just an ad hoc assumption, to mention only one.
The next diagram (also from LIBBRECHT 's website) gives values of vapor supersaturation in percents, for different temperatures, that is,
( P water - P ice ) / P ice x 100%,
typically found in dense clouds. The diagram can be seen HERE
or one can inspect an enlargement of it :
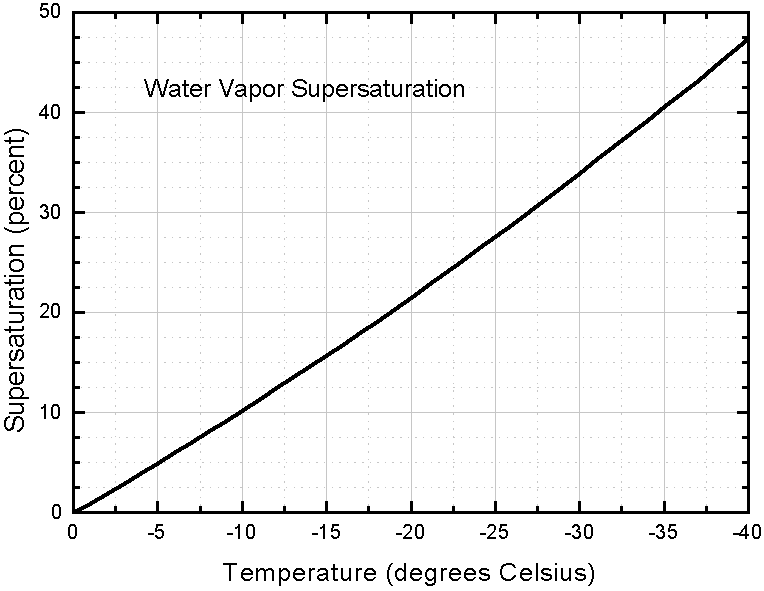
Supersaturation levels higher than these are probably quite unusual in the atmosphere.
To explain the just given measure for vapor supersaturation : If the actual pressure of the water vapor measured (not necessarily the equilibrium vapor pressure) were twice the equilibrium water-vapor pressure of ice, then we would get
( 2P ice - P ice ) / P ice = P ice / P ice = 1 = 100% supersaturation.
So we see in what way supersaturation is presented.
Unstable Crystallization in Dendritic Ice Crystals (branched snow crystals, windowpane frost) from a thermodynamic viewpoint. Comparison with the Bénard Instability.
The resulting dissipative structure of the Bénard process (discussed in the previous document), that is, the highly organized convection cells, is maintained by a potential difference or, equivalently, a potential fall, which in this case is a thermal potential difference, namely a difference in temperature between top and bottom sites of the fluid layer. This difference and its appropriate magnitude, which is the 'motor' that keeps the structure going, must be actively maintained from without (by heating the bottom site) if the existence of the resulting structures is to be continued.
Another example of a non-linear far-from-equilibrium system is the Belousov-Zhabothinsky Reaction (discussed in the document "Non-living dissipative systems" (first Series of documents) in First Part of website ). Here certain chemicals are constantly being imported into the reaction theatre and others are exported. So here we could speak of a chemical potential difference or fall, constantly being maintained from without.
In the case of normal crystallization from a melt the 'motor' is, like in the Bénard process, a thermal potential difference or fall, namely supercooling. This also must be actively maintained from without (by exporting heat from the melt) if continued crystallization is to be maintained. The range of this potential is :
supercooling temperatures ==> melting point.
In the case of normal crystallization from a liquid solvent, say, the crystallization of common salt (NaCl) from its aquous solution, there are two important differences that determine the crystallization. These are undercooling and supersaturation. If we crystallize salt from its aquous solution at normal temperatures and pressures, we are working well within the undercooling range of salt, that is, far below its melting point. For the possibility of the crystallization process, undercooling means -- according to me -- nothing more than that the process is well within the stability range of solid salt. So this is, what we could say, a conditio sine qua non (absolutely indispensable, but not necessarily sufficient condition). The other condition is the supersaturation of the solution with respect to the solute, which constitutes the potential difference or fall, which in turn will be the 'motor' of the crystallization process. The range of this potential is :
degrees of supersaturation ==> saturation.
Supersaturation of a solute in a solvent is equivalent to overcrowding of the solute particles in the solution, that is, the particles have become so close together that their mutual distances have become such that their attractive forces become dominant. When crystallization nuclei are present (crystal embryos of sufficiently large size, that have happened to form, or other (larger) particles (also) providing an energy well), crystals of the solute are formed and grow.
The degree of supersaturation, effected by a given amount of solute in a given volume of solvent, in principle depends on the nature of the solute, that is, the intrinsic mutual attracting force of its particles. But the nature of the solvent determines when this force gets the upper hand : When a solvent can hold less an amount of solute per unit volume (that is, when the solute is less soluble) than another solvent can, it apparently allows the particles of the solute to get closer to each other at already a lower overall concentration, that is, solute and solvent don't mix so well, resulting in local subvolumes of high (local) concentration of solute, which eventually leads to its precipitation.
In an undersaturated liquid solution generally no crystals (of the solute) can develop.
Crystallization from a gaseous solvent.
Natural snow crystals originate directly from water vapor in the air (with perhaps some very brief intermediate and transient liquid state). And water vapor in the air is in fact a solution of water vapor in the air (minus water vapor). So also here we have crystallization from a solution, albeit a gaseous solution : both the solute (water vapor) and the solvent (air minus water vapor) are gaseous. And also here we have as conditio sine qua non a supercooling : The temperature must be below water's freezing point. So also here the 'motor' of the process (crystallization) is supersaturation. The range of this potential is here again :
degrees of supersaturation ==> saturation,
here, however, supersaturation with respect to ice, not with respect to liquid water.
But how exactly are natural snow crystals generated in the atmosphere?
We can answer this question in a preliminary way only, while basing it on the relevant expositions in the website of Y. FURUKAWA (after 1997) :
Let us start with air at some below-zero temperature in which undercooled water droplets are present. These water droplets partially evaporate, resulting in roughly the saturation pressure ps of the water vapor with respect to liquid water, or (resulting) in an approach to such a pressure (these pressures are always partial pressures, that is : the pressure the water vapor would have if it were the only constituent of the air). See for this also LIBBRECHT's website, SnowCrystals.com, Snowflake Designer's Page, first Section.
The air, and thus the water vapor phase, has a below-zero temperature such that it can be assumed that this water vapor phase is supersaturated with respect to ice.
Among the (supercooled) water droplets, some very small ones (of about 0.0001 mm in diameter, according to FURUKAWA) have turned into (small) spherical ice pellets. The water vapor (being supersaturated with respect to ice) will now diffuse away from the (remaining) droplets and deposit itself onto the surface of these small ice pellets (i.e. the vapor directly turns into ice). The latter then develop crystal faces (where fast-growing faces bounded by tapering slower-growing faces finally disappear again), resulting in a snow crystal.
Let us now concentrate further on this crystallization of ice crystals directly from water vapor in the air.
When the potential difference degree of supersaturation ice ==> saturation ice (at a defined undercooling temperature) is relatively small, we get near-to-equilibrium crystallization. Depending on the ambient temperature we then obtain either smooth hexagonal prisms (columnar shape) or smooth hexagonal plates (which both are temperature-dependent (morphological) habit types).
When, on the other hand, this potential difference is large : high degree of supersaturation ice , we get far-from-equilibrium crystallization, yielding complex crystals, such as branched plates.
A high degree of supersaturation turns out to be most effective at temperatures around -150C. This is because in this temperature range air can contain a maximum amount of water vapor, before being saturated with respect to water. So here the air can contain very much water vapor while still being in a condition of relatively low instability. Thus there is much water vapor available for crystallization, and the process can proceed fast.
For equilibrium thermodynamic processes we can define thermodynamic potentials such as free energy and entropy.
For near-to-equilibrium thermodynamic processes we have the minimum entropy production as a thermodynamic potential.
But for far-from-equilibrium thermodynamic processes (such as the Bénard instability) we have no thermodynamic potentials anymore. Such a system may still evolve to some steady state, but in general this state can no longer be characterized in terms of some suitably chosen potential ( PRIGOGINE & STENGERS, Order out of Chaos, p.140 of the 1986 Flamingo edition).
And indeed, in the process producing dendritic crystals, the surface area of the crystal, and therefore the free surface energy Gs , increases -- as it seems, exponentially -- while the volume of the crystal remains relatively small. So there is no thermodynamic potential toward whose extreme the system can go. In this case the Gibbs free energy increases -- as it seems without limit -- let alone that it decrease toward a minimum. The process nevertheless keeps going as long as the high supersaturation and diffusion of water vapor toward the crystal is maintained.
Such a process (as are all processes) is in fact a series of energy conversions, and will as such be described in the next large Section, which is, consequently, concerned with energy statics (intrinsic energy of states), energy dynamics (forces), and energy kinetics (rates of change in processes), of crystal generation and growth.
The Crystallization Process seen as a series of Energy Conversions along the trajectory of an Energy Flux.
In order to understand the crystallization process still further -- beginning with near-to-equilibrium crystallization, but aiming at far-from-equilibrium crystallization (if the latter indeed exists as assumed to be the case in the formation of dendritic crystals) -- we must now, armed with our acquired knowledge of general thermodynamics, see how the process can be seen as a flux of energy -- between two levels of potential energy [from high to lower potential energy] -- a flux in which one or more energy conversions take place, such as modality transformations, which are transformations from potential energy to actual energy or vice versa, and quality transformations, which are transformations between several forms of energy (heat energy, mechanical energy, radiation energy, chemical energy, etc.).
For this we must consider the following things :
Energy is the capacity to do work.
It occurs in different versions, forms, or qualities, viz., heat, motion, chemical energy, electrical energy, etc.
It also occurs in two different modalities, viz., potential energy and actual energy (see below).
The different qualities (and modalities) are energetically equivalent and obey the First Law of Thermodynamics : The conservation of (the amount of) energy in all transformations.
The capacity of bringing forth an effect is the effectiveness of a given energy form.
The intensity of an energy form is its effectiveness per unit volume.
The Second Law of Thermodynamics states that in every energy transformation the intensity decreases (yet another equivalent formulation of this Law), and -- in accordance with the First Law -- the extensity increases. This latter is the dissipation of energy, or, equivalently, the increase of entropy.
The different qualities (forms) of energy show a scale of intensities. There, heat has the lowest intensity. And because entropy increase is dissipation and leveling-out of energy, we can say that the Second Law states that in all transformations the amount of heat will increase at the expense of all other energy forms, and effects the leveling-out of energy differences that may obtain between different sites.
Energy can be in a state of giving off work (which is just some specific energy conversion from one form of energy into another) and can then be visible in the form of motions or be visible in some other way. Energy in this state is then called actual energy.
Potential energy (in fact a theoretical concept to allow for the conservation of energy during processes and (thus) energy transformations) on the other hand, is not characterized by some velocity as an expression of motion, but is characterized by the position of the system with respect to its environment, or by the positions of its parts with respect to each other, and is therefore also called 'static energy', or 'energy of position', or 'configurative energy'.
Because the stock of potential energy is not directly observable, we can only conclude to the existence of this stock and its magnitude, by measuring the released actual energy. We then make use of the First Law of Thermodynamics.
We can thus investigate different states of matter with respect to this energy stock or potential energy, that is their intrinsic energies belonging to certain conditions (such as the liquid state of some substance under specified conditions of temperature and pressure).
We could then compare :
Let us now then look to the results obtained regarding the potential energy stock (work stock) of states (PRZIBRAM, Ibid., pp.102) :
The states of Dispersion
Generally the amorphous state possesses more potential energy (work stock) than the corresponding crystalline state (One could, for example, compare a glass and its corresponding crystalline state of a given substance). The amount of heat, released during (the process of) spontaneous dissolution (of some solute into a solvent) -- and heat is r e l e a s e d because in this (supposed) case the solution (that is, the solute in its state of being dissolved) has lower potential energy than the solid, as solid, in the solvent -- is always greater in the case of amorphous states of solutes (being dissolved in a solvent), than it is in that of the corresponding crystalline states (that is, when we dissolve crystals instead of amorphous masses) (PRZIBRAM, p.102).
So the crystal had, during its formation (at some earlier time), already released a part of the potential energy (heat of crystallization) ( This we must reformulate as follows : A part of the total potential energy of the solution was released [namely from there where the crystal formed] ). It is released in the form of heat.
The states of Aggregation
Here we compare the liquid state of some given substance with its corresponding solid state.
A liquid has -- when not considering stability differences under certain conditions -- a larger stock of potential energy (work stock) than its corresponding solid (We can, for example, compare liquid water at say, 200 C [and thus well within its stability range] and ice at say, -100 C [also well within its stability range] ). This can be shown by the following :
A liquid more easily and more extensively establishes contact with a given solid substance and thus reacts faster with it than when it were itself a solid. Still faster do two substances react when both are in their liquid state.
So if indeed the liquid state possesses more potential energy (work stock) than its corresponding solid state, the latter must effect the release of this difference when it forms from its liquid state (that is, the potential energy of part of the liquid, namely that part of it that is involved in the solidification is released), like the crystal when it formed from the amorphous state (As regards the latter, for example the formation of crystals from a glass).
Indeed, when one decreases the temperature, and finally arrives at the solidification point ( = melting point) of the substance, the heat of fusion -- that was taken up during melting for randomizing the material (randomizing the configuration of its particles) -- is released as soon as this solidification actually takes place, and which retards the process of solidification (PRZIBRAM, Ibid., p.103).
During the heating of a solid, on the other hand, heat is taken up to increase the temperature (that is, to increase the average kinetic energy of the particles), but when the melting point is reached the heat is no longer used for temperature increase, but for randomizing (the configuration of) these particles. This latter imported energy then is the heat of fusion and is thus converted into configurative energy, that is, energy of position -- potential energy.
Also the transition from solid crystals to liquid crystals entails import of heat to partly randomize the particles of the solid crystal (resulting in the liquid crystal). So also the liquid crystal has more potential energy than the corresponding solid crystal (of the same substance).
The states of Form or Shape (Morphe)
Indeed, one can, and should, consider the intrinsic form or shape of some material as representing a state of it.
Because a specific (morphological) form, representing itself as a set of robust and constant external and internal boundaries, is possible in the solid state only (and less robustly so in the semiliquid state as we find it in organisms), the taking on of such a form will, generally, be accompanied by a decrease of potential energy.
Crystals are compacted into a smaller volume than an eaqual mass of their corresponding amorphous states. Generally this is also the case for solids with repect to their corresponding liquid state, but there are exceptions : At 00 C liquid water is more compact (more dense) than ice. Nevertheless the taking on of a definite shape or form entails a contraction and compaction of some sort (because the volumetric expansion of ice is not just a simple expansion, but a definite ordering of particles from a less ordered (but not totally disordered) state as it is found in liquid water).
Because in all cases of transformation from the liquid or gaseous state (generally : from the fluid state) to the solid state the emergence of form boundaries (which are surfaces) is involved, the relevant energies, engaged in such transformations, can be categorized as surface energies. The usual relevant surface energy (of first sort) consists of two factors :
It is clear that the situation in the case of dendritic crystals must be different, like the case of organisms :
Dendritic crystals are expected to be comparable in this respect (high potential energy stock) with organisms. At least their shape is very light (very open, very uncompacted), with a large surface area, and thus a large number of 'dangling' bonds (i.e. unsatisfied chemical bonds [that is, unsatisfied covalent-, ionic-, hydrogen-, or other bonds] ) and consequently possessing a large amount of this kind of surface energy.
We will now investigate where the potential energy stock (or increase of potential energy) comes from, and in what way this energy is employed in the formation of crystals.
Origin of potential energy stock
First we can ask in what way the form-generating process at work in crystallization -- ordering of particles, resulting in a crystal lattice -- obtains its form-generating energy, and in virtue of what it exhausts its resources of energy. So here we're going to speak about the form-generating energies that become available by some increase in potential energy of the medium that is about to form crystals.
Because free form-generating energy does not exist (i.e. exist outside the crystal's molecules or atoms), a crystal cannot just take in form-generating energy from without (that is, from the environment, here from the solution, vapor or melt). A transformation of received energy of some kind into form-generating energy is necessary (PRZIBRAM, Ibid., p.108).
(Added) heat (that is, intake of actual energy which remains actual energy) will, however, play an important role in the rate of crystal growth : Particles then have a higher (average) kinetic energy which promotes the supply of these particles toward the surface of the growing crystal.
A stockpiling of potential energy (without any modality transformation, here thus : intake of potential energy that remains potential energy), is accomplished by import of fresh nutrient material into the nutrient solution, and its transport -- by diffusion (in virtue of a concentration gradient) -- to the surface of the growing crystal (where the mentioned gradient originates from the decrease of the nutrient concentration near the crystal surface as a result of deposition onto the latter). Also concentration currents, as a result of local heating, aid in transporting nutrient material to the crystal (which we can see as an import of fresh nutrient material, and thus of potential energy).
So these are the ways in which a crystal obtains its form-generating energy (PRZIBRAM, Ibid., p.108).
REMARK :
I see as yet no way to r i g o r o u s l y incorporate these considerations inspired by PRZIBRAM regarding the form-generating energy that must be available in order for crystallization to get going, into the general thermodynamic framework (they can only be incorporated loosely). Nevertheless they are interesting and important. PRZIBRAM in his text tries to demonstrate the general thermodynamic equivalence that should obtain between crystals and organisms ( This is to counteract ideas about a fundamental difference between inorganic and organic beings in this [thermodynamic] respect (or any other respect for that matter) ). Regarding the form-generating energy that is assumed to be needed in crystallization, we should realize that every process is in fact just a series of energy transformations or conversions (potential energy into actual energy, heat energy into mechanical energy, chemical energy into heat energy, but of course also triplets or larger series of conversions). And in all these conversions, energy as such is never lost. ( End Remark )
In the present thermodynamic considerations we are especially aiming at an understanding of the generation of dendritic crystals. And because we hope to accomplish this by investigating the generation of branched snow crystals and windowpane frost -- and then generalizing these special cases -- we will have to do with crystal formation directly from a vapor (water vapor ==> ice crystals). And this means that we have to do with a solution (in this case a gaseous solution) instead of with a melt (For the nature of solutions see Part XXIX Sequel-23 ).
Let us restate some features of solutions, in order to consider how the potential energy stock is obtained in the case of crystallization from a solution. It goes like this : We first show under what thermodynamic conditions dissolution is possible. Then we show in what way a solution can stockpile potential energy, necessary for crystallization from this solution.
Initially (that is, before solution takes place) we have a spatial separation of solute from solvent particles (that is, we have a crystal lying in a solvent). And although the particles of the solute, still in its solid state, are held together by attractive forces, these forces are superseded by a somewhat stronger interaction between them (that is, the solute particles) and the solvent particles, causing the solute to be dispersed throughout the solvent. If the concentration of the dissolved solute is such that it can exist in equilibrium with excess undissolved solute, then the solution is said to be saturated. In the case of liquid solutions (say that of salt in water) we speak of the equilibrium concentration of the solute, while in the case of gaseous solutions (say that of water vapor in the air) we speak of the equilibrium vapor pressure of the solute (with respect its liquid state or with respect to its solid state).
So before dissolution has taken place we have an initial separation of solute particles (constituting a crystal) from the solvent particles, while at the same time the solvent particles attract the solute particles, and the solute particles attract the solvent particles. This means that we have a potential energy of position, which causes the particles of the solvent to 'fall' to the particles of the solute and vice versa, that is they mix, and energy is released. The potential energy (difference) has been converted to movement of the solute and solvent particles toward each other. So when the particles are finally mixed up the potential energy difference (expressed by the initial distance between solute particles and solvent particles) is annihilated (like in the case of a falling stone), and is released. That is, energy is released.
This energy is now used to separate solute particles from each other (that is getting them out of the (tight) crystal lattice), and to separate solvent particles (in order to provide for the introduction of solute particles between them).
But in certain cases (that is, for certain substances) this energy is not sufficient to do the job. That is, in such cases the net attraction between solvent and solute particles is only very small. Nevertheless dissolution can still take place, because there is yet another factor that encourages dissolution : A solution is more disordered than either the pure solvent or solute and, therefore, the solution is a more probable state for the substances (the solvent and the solute). Dissolution frequently occurs thanks to an entropy increase, in spite of the fact that (in the mentioned cases) solvent-solute attractions are not sufficiently large to counteract the energy required to separate solute particles from each other, and solvent particles from each other (OUELLETTE, R., Introductory Chemistry, 1970, p.172-174).
The heat evolved or absorbed when the solute dissolves to produce a saturated solution is called the heat of solution. If heat is evolved when solution occurs, the heat of solution is a negative quantity (the heat of solution represents the difference [increase or decrease] in enthalpy DELTA H [that is,  H ] ) :
H ] ) :
solute + solvent = solution + heat ( DELTA H < 0, negative heat of solution).
heat + solute + solvent = solution ( DELTA H > 0, positive heat of solution).
As has been said, in a g a s e o u s solution saturation is expressed in terms of vapor pressure of the solute, when the latter is in equilibrium with either its liquid state (vapor pressure with respect to liquid) or with its solid state (vapor pressure with respect to the solid). In the case of a g a s e o u s solution we thus also have a heat of solution ( DELTA H ), which can be negative or positive. And also here this is only one factor deciding whether dissolution will proceed spontaneously. The other factor is the entropy change between pure solvent and pure solute on the one hand and the solution on the other. This is the entropy term T ( DELTA S ) in the definition of the Gibbs free energy DELTA G :
where DELTA G is the potential energy (difference).
So when, finally DELTA G is negative, the process of dissolution will proceed.
So we have explained in terms of energetics the dissolution process. Now we must see how such a solution itself can become a stock of potential energy that makes possible crystallization. Well, this potential energy stock is provided by continued dissolution of solute material into the solvent, (way) b e y o n d the saturation point (and for gaseous solutions, a b o v e the equilibrium vapor pressure). That this is possible is evident by all the actually existing cases of supersaturation. Supersaturated solutions can exist in a metastable condition because there exist small energy barriers that prevent them from spontaneously demixing (precipitation of the solute from the solvent). Such a case of supersaturation makes the solution -- as solution -- unstable (metastable), and as soon as the mentioned energy barriers are removed, for example by the introduction of suitable condensation nuclei or crystallization nuclei, the solution will demix and a part of the (amount of) solute will be precipitated. The supersaturation of the solution thus is the potential energy stock, and in advance of the next section (which is about the expenditure of the acquired stock of potential energy) we have explained why this potential energy, as it has become stockpiled by supersaturation, indeed represents the potential energy fall that is needed to make the crystallization process feasible. The same applies mutatis mutandis with respect to melts : here supersaturation must be replaced by undercooling.
Employment of the potential energy stock in the form-generating process of crystallization. ( PRZIBRAM, Ibid., p.112/3 )
We now consider the expenditure of the potential energy stock for keeping the form-generation process going.
The decrease of this potential energy, as this energy is present in the solution, vapor, or melt, does do the 'work' in the form-generating process
just like -- now not a form-generating process -- the decrease of potential energy results in the falling motion of an object possessing that potential energy [And when this object hits the ground inelastically, the kinetic energy of the whole object, and thus the difference in potential energy (from which that kinetic energy was formed by energy conversion) -- measured from the height from where the object was released to the ground where it lands -- is converted either into active heat (increase of the average kinetic energy of the particles of the place of impact -- resulting in an increase of temperature) or, when it causes melting at the place of impact, into latent heat (randomization of the configuration of the particles of the place of impact) ].
Indeed, something analogous to what has just been described we see in crystallization :
First there is a solution or melt possessing -- under the appropriate circumstances of supersaturation and undercooling -- a higher potential energy than the corresponding crystals under the same conditions. So we have a potential energy fall (difference in potential energy). Then this potential energy difference is converted into collective kinetic energy of the 'nutrient' particles ('feeding' the crystal), resulting in their ordering into a crystal lattice, and then, finally, this collective kinetic energy is converted into heat, that is, heat of crystallization, which is, in the case of crystallization from a melt [heat released], equal in magnitude to the heat of fusion [heat absorbed] in melting, and which [heat of crystallization] is, in the case of crystallization from a solution [heat released], equal to the absorbed heat of solution, provided that the substance that initially had been subjected to dissolution (that is, was used for dissolution) is (for this comparison to be valid) exactly of the same chemical type as that of the crystalline phase that has subsequently developed (crystallized) from the solution, for example when we consider the thermodynamic comparison between the crystallization of Na2SO4 .10 H2O and the dissolution of just this Na2SO4 .10 H2O and not of Na2SO4 (dry sodium sulfate), as will be explained below.
The r e l e a s e of the heat of fusion (which [heat of fusion] itself is latent heat, that is, potential energy), increasing (as a result of this releasing) the average kinetic energy of the particles [which is actual energy], and consequently, increasing the bulk temperature ( Thus, all in all, the conversion of the potential energy -- heat of fusion -- [that as such did not increase the temperature during melting, but was used to randomize the configuration of particles] into active heat ), generally decelerates the process of solidification (of the melt).
In a solution (gaseous, liquid, or solid solution), however, the release of heat of crystallization effects a higher rate of transport of nutrient material to the crystal surface. This transport is relevant and necessary because in a solution the solute particles, which are about to gather and conform into a crystal lattice, are separated from each other and from the surface of the growing crystal by solvent particles.
Generally, the latent heat of fusion, before it is released to the ambient fluid, is used for the form-generating process, and after having done the 'work' ( = letting the particles fall into their favorable positions [lattice points] ), it is transformed into (the extra) undirected kinetic energy (that is, its increase) of the particles of the ambient fluid, and thus is dissipated (over this fluid) ( PRZIBRAM, Ibid., p.113 ).
Perhaps we could rephrase all this a little bit :
The (higher) potential energy of the fluid (solution, melt) consists in the fluid being disorganized, i.e. the (ever changing) positions of the particles being such that the system is, at conditions of supersaturation or undercooling, far away from its stable state, which (stable state) consists in the lowest energy congfiguration of its particles, which configuration is the organization into some definite lattice. Normally we can recognize this (higher) potential energy already by the fact that the particles of the solution or melt 'stand' farther away from each other than they do in the corresponding solid. Water, however, is, as we know, an exception : When liquid water freezes, it expands, that is, the particles settle at places such that they come to stand farther apart from each other (Of course, in the formation of ice directly from water vapor, the particles do come closer together). In the case of liquid water freezing to ice, we must imagine that at the freezing point the system (of particles) is like a spring that is pressed (instead of stretched, like in almost all other cases (other substances)), that is, has ended up in a situation such as if being pressed. So if we let the system freeze, we allow this tension to be relaxed, and the system spontaneously expands and organizes its particles into their energetically favorable positions (lattice points). So also in this case we see a decrease of potential energy. With substances that differ in this respect from water, the 'spring' is, under conditions of supersaturation or undercooling, initially held in a stretched position, and upon letting them crystallize or freeze (by adding suitable nuclei) we let go this stretching, and this results in the system to spontaneously contract (yielding crystals whose density is higher than that of the corresponding melt). In all cases, whether it will be water or any other substance, the spontaneous transition from liquid to solid involves relaxation.
And as long as this relaxation hasn't yet happened (still at conditions of supersaturation or undercooling), the system has high potential energy. Upon crystallization this potential energy is converted into directed kinetic energy of particles resulting in their being taken up into a crystal lattice, that is, the particles 'fall' into their energetically favorable positions, either by a structured widening, as in the freezing of water, or by a structured compaction, as in most other cases, where both processes (widening and compaction) are relaxations.
Generally we must say that for a process (and thus also crystallization) to be possible, a difference in potential energy levels must be present, where the system possesses the higher level. However, the ultimate condition that must be fulfilled for a process to be possible is that the net entropy of the system-as-a-whole would, as a result of this process, increase. Only then we have the ultimate potential energy difference, that determines the feasibility and direction of the process.
Considering crystallization from a melt : After the particles have fallen into their favorable positions, their directed kinetic energy (which has led them toward these positions) will be converted into undirected, randomized kinetic energy of the particles of the melt, which energy now is just heat (as it is precisely the case with a stone fallen from some height above the ground, that upon hitting the ground inelastically, creates heat at the site of impact). That is, the already randomized average kinetic energy of the particles of the melt has just increased, the temperature goes up (but quickly goes down again, as it is in the oscillation described above [this low-amplitude oscillation in fact represents the constant temperature at which the liquid state (melt) and the solid state (crystal) are in equilibrium] ). And if this released heat (of crystallization) is effectively removed from the system, or at least from the actual site of crystallization, the latter can go on at a constant temperature (heat removed, heat evolved by continued crystallization), which is the solidification point of the given substance, and (is) also the (mentioned) temperature at which the two phases are in equilibrium with each other.
In the case of crystallization from a solution (as in crystallization of a some salt [say, potassium chloride, sodium sufate, or whatever] in water, or crystallization of water vapor in the air [as is the case in snow-crystal formation] ) the situation is somewhat different from crystallization from a melt
(
For all this we must bear in mind that the equation ( where we will write
 for DELTA, meaning "change of " )
for DELTA, meaning "change of " )  G =
G =  H - T
H - T S
(where G = Gibbs free energy, H = enthalpy, T = absolute temperature, and S = entropy)
determines the feasibility in principle for some given transformation. In our case such a transformation could be (1) the melting of a given substance, (2) the solidification (crystallization) of that substance from its melt, (3) the dissolution of a given substance in some solvent, or (4) the crystallization of this substance from its solution
)
:
S
(where G = Gibbs free energy, H = enthalpy, T = absolute temperature, and S = entropy)
determines the feasibility in principle for some given transformation. In our case such a transformation could be (1) the melting of a given substance, (2) the solidification (crystallization) of that substance from its melt, (3) the dissolution of a given substance in some solvent, or (4) the crystallization of this substance from its solution
)
:
The solubility of a solute in a solvent is its concentration in a saturated solution, where the concentration is the amount of dissolved solute, which can be measured in several ways (grams of solute / grams of solution, moles of solute / liters of solution, humidity, etc.). The solubility changes with temperature, and either increases or decreases with increasing temperature depending on the nature of the solute for a given solvent. The heat evolved or absorbed when the solute dissolves to produce a saturated solution is, as we know, the heat of solution. If, depending on the nature of the solute, heat is evolved when solution occurs, the heat of solution, DELTA H , is a negative quantity (where it codetermines the value of the change in the Gibbs free energy with respect to spontaneous dissolution). If, on the other hand, (for other solutes) it is absorbed, DELTA H is positive (where it also codetermines the value of the change in the Gibbs free energy with respect to spontaneous dissolution). So it seems that if we (conceptually) reverse the process, that is, if we let a solute crystallize from a solution, heat can be absorbed, or (in the case of other solutes), heat can be released.
When, upon dissolution, heat is absorbed ( DELTA H > 0 ) , as in, say, the dissolution of potassium chloride ( KCl ) in water (See the solubility curve for KCl further below ), this heat is released again upon crystallization ( DELTA H < 0 ) . So this latter enthalpy term contributes to making the Gibbs free energy DELTA G negative in : DELTA G = DELTA H - T ( DELTA S ) for crystallization feasibility. So in this case we have the same situation as in the case of solidification from a melt : There heat is always evolved because there we have only a one-component system, that is, there is no interaction between, say, a solute and the solvent. And there (that is, in solidification from a melt) we have always relaxation taking place with a release of heat (that in melting was the absorbed heat of fusion, and now is that same heat, released as heat of crystallization).
When, on the other hand, heat is released upon dissolution ( DELTA H < 0 ) , as in, say, the dissolution of dry sodium sulfate ( Na2SO4 ) in water, this heat is apparently absorbed again upon crystallization ( DELTA H > 0 ). So here we have apparently a case of crystallization where heat is taken in, instead of being released, that is to say, the stability (under these conditions) of crystalline Na2SO4 is less stable than its solution. Thus the enthalpy term, which is now positive, works against the Gibbs free energy DELTA G becoming negative in : DELTA G = DELTA H - T ( DELTA S ) for crystallization feasibility. So it seems that here the entropy term T ( DELTA S ) must counteract this enthalpy term in order to make DELTA G negative. Thus when crystallization of this salt (sodium sulfate) actually occurs (indicating that under the given circumstances it was feasible anyway), this entropy term should then more than compensate for the positivity of the enthalpy term. How this is accomplished (which could be a problem, because a crystal has lower entropy than its solution), might be explained as follows : In fact it (that is, the alledged compensation) is not accomplished at all : The entropy of the resulting crystal is not higher than that of its solution under the same circumstances, and the enthalpy term must be negative. How could that be?
For this to explain we must come to know a little bit more about hydrates and anhydrites of salts. For us it is sufficient to see how things are in this respect in the case of sodium sulfate.
Sodium sulfate can exist in several forms, depending on temperature and pressure :
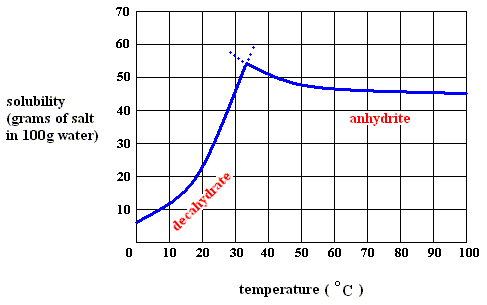
Figure above : Solubility of solid sodium-sulfate decahydrate (left), and of solid sodium-sulfate anhydrite in water as a function of temperature (curves are approximate).
If we dissolve more and more decahydrate in water, at a temperature below 32.60C, say at 200C, we will eventually obtain a saturated solution, that is, a solution that is saturated with respect to the decahydrate at that temperature. If we now increase the temperature, the solubility of the decahydrate increases (according to its solubility curve). So we can dissolve still more of it in the same volume of water. At 32.60C we can dissolve a maximum amount of decahydrate, because as soon as we (while still preparing a saturated solution) get past 32.60C, our solution suddenly becomes supersaturated with respect, not to the decahydrate, but to the anhydrite : The solution went, upon passing 32.60C, from a saturated solution with respect to the decahydrate to a supersaturated solution with respect to the anhydrite. So when suitable crystallization nuclei are present, solid anhydrite will be precipitated (All the above is according to a textbook of inorganic chemistry "Beginselen der Chemie", by Van ERP, p.34 (but is expected to be found in any such textbook]), and the solution will now (that is, at a temperature above 32.60C ) be saturated with respect to the anhydrite. So we see the temperature-stability regions of the decahydrate and the anhydrite, lying to the left of, resp. to the right of, 32.60C.
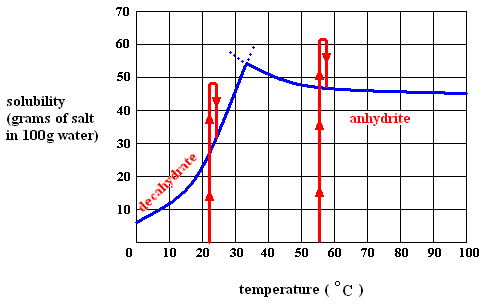
Figure above : Dissolution, saturation, supersaturation and crystallization of the decahydrate of sodium sulfate and of the anhydrite of sodium sulfate.
So while in crystallization from a melt, the released heat must be led away, and thus letting the temperature to remain constant (and this must be so, if we want to use the Gibbs free energy as a thermodynamic potential, whose minimal value is the attractor of the system), the same is the case in crystallization from a solution of substances like potassium chloride or (at a temperature below 32.60C ) the decahydrate of sodium sulfate : the heat that was absorbed upon dissolution is released again upon crystallization of these substances. In the case of crystallization from a solution of the anhydrite of sodium sulfate, however, things are a bit different : Upon dissolution at a temperature above 32.60C heat was released. So it cannot make up a potential energy stock. However, upon (forcibly) supersaturating the solution of the anhydrite, heat must be absorbed (see below), and thus a potential-energy stock is built up nevertheless. Upon crystallization of the anhydrite this absorbed heat is released again. And to keep the crystallization going, supersaturation must be maintained.
Let us summarize the cases of : (1) melting of some crystalline substance, (2) crystallization of that substance from its undercooled melt, (3) dissolution of a substance like potassium chloride in water, (4) crystallization of this substance from its supersaturated aquous solution, (5) dissolution of sodium-sulfate decahydrate in water below 32.60C, (6) crystallization of this substance from its supersaturated aquous solution below 32.60C, (7) dissolution of the anhydrite of sodium sulfate (dry sodium sulfate) in water above 32.60C, (8) crystallization of the anhydrite from its supersaturated aquous solution above 32.60C, (9) dissolution of a gas in a (mixture of) gas(es), such as the dissolution of water vapor [solute] in the air [solvent] (resulting in a gaseous solution), (10) crystallization of a solid from a gaseous solution, such as the crystallization of snow crystals from water vapor in the air
( where  = DELTA = "change of " ) :
= DELTA = "change of " ) :
 G =
G =  H - T
H - T S for state transition : crystalline phase ==> melt.
S for state transition : crystalline phase ==> melt. H is positive [heat absorbed], because that will be more than compensated for by the increase in entropy of that part of the solid that is in the process of melting (the particles of the solid become randomized with respect to their position), T
H is positive [heat absorbed], because that will be more than compensated for by the increase in entropy of that part of the solid that is in the process of melting (the particles of the solid become randomized with respect to their position), T S is positive, guaranteeing the negativity of
S is positive, guaranteeing the negativity of  G of the feasibility of the molten condition. That is to say, melting is possible under these conditions (temperature above melting point). Here the absorbed heat, together with the increase of the entropy of the system makes up the potential-energy surplus (potential-energy stock) as the melt (later) becomes undercooled.
G of the feasibility of the molten condition. That is to say, melting is possible under these conditions (temperature above melting point). Here the absorbed heat, together with the increase of the entropy of the system makes up the potential-energy surplus (potential-energy stock) as the melt (later) becomes undercooled. H positive), and thus lowering the entropy of the surroundings (from where this heat was taken), this must -- in accordance with the Second Law of Thermodynamics -- be more than compensated for by the increase of entropy, there where the solid is melting ( T
H positive), and thus lowering the entropy of the surroundings (from where this heat was taken), this must -- in accordance with the Second Law of Thermodynamics -- be more than compensated for by the increase of entropy, there where the solid is melting ( T S positive).
S positive).
 G =
G =  H - T
H - T S for state transition : melt ==> crystalline phase.
S for state transition : melt ==> crystalline phase. H is negative : Under conditions of undercooling the crystalline phase is more stable than the corresponding liquid phase. And this more than compensates the decrease of entropy of the subvolume where the crystals are formed.
H is negative : Under conditions of undercooling the crystalline phase is more stable than the corresponding liquid phase. And this more than compensates the decrease of entropy of the subvolume where the crystals are formed.  H means that the crystallization process in this case is exothermal. It uses the (above mentioned) potential-energy stock of the melt.
H means that the crystallization process in this case is exothermal. It uses the (above mentioned) potential-energy stock of the melt. H also means that the entropy of the surroundings will increase, and -- satisfying the Second Law of Thermodynamics -- more than compensates for the decrease of entropy, there where the crystalline phase appears ( T
H also means that the entropy of the surroundings will increase, and -- satisfying the Second Law of Thermodynamics -- more than compensates for the decrease of entropy, there where the crystalline phase appears ( T S negative).
S negative).
 G =
G =  H - T
H - T S for state transition : crystalline phase ==> aquous solution ( KCl, etc.).
S for state transition : crystalline phase ==> aquous solution ( KCl, etc.).
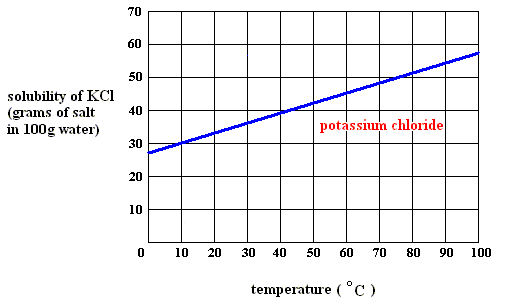
As long as the solution (of potassium chloride) is undersaturated, the dissolution process will continue (if enough material is available in the system). Heat is absorbed (according to the solubility curve of such a substance),  H is positive, but the entropy term more than compensates this, because the solution (which is a mixture) has a much higher entropy than the pure substances (solute and solvent) being separated from each other, so the change of (Gibbs) free energy for dissolution feasibility is negative (and thus making dissolution possible). Here the absorption of heat together with the increase of entropy of the system makes up the potential-energy surplus (potential-energy stock) as soon as the solution becomes supersaturated.
H is positive, but the entropy term more than compensates this, because the solution (which is a mixture) has a much higher entropy than the pure substances (solute and solvent) being separated from each other, so the change of (Gibbs) free energy for dissolution feasibility is negative (and thus making dissolution possible). Here the absorption of heat together with the increase of entropy of the system makes up the potential-energy surplus (potential-energy stock) as soon as the solution becomes supersaturated.
Although heat is absorbed (  H positive) because of the dissolution process, and the entropy of the surroundings must, therefore, decrease, for the system the entropy increases, and according to the Second Law of Thermodynamics the latter must be such that the net overall entropy increases.
H positive) because of the dissolution process, and the entropy of the surroundings must, therefore, decrease, for the system the entropy increases, and according to the Second Law of Thermodynamics the latter must be such that the net overall entropy increases.
 G =
G =  H - T
H - T S for state transition : aquous solution ==> crystalline phase ( KCl, etc.).
S for state transition : aquous solution ==> crystalline phase ( KCl, etc.). H is negative. So the enthalpy term already contributes to making the (Gibbs) free energy difference
H is negative. So the enthalpy term already contributes to making the (Gibbs) free energy difference  G for crystallization feasibility negative, and more than compensates for the decrease in entropy of that part of the solution where crystals are formed ( T
G for crystallization feasibility negative, and more than compensates for the decrease in entropy of that part of the solution where crystals are formed ( T S negative). So also here the crystallization process is exothermal. It uses the (above mentioned) potential-energy stock of the solution.
S negative). So also here the crystallization process is exothermal. It uses the (above mentioned) potential-energy stock of the solution. H also means that the entropy of the surroundings will increase, and -- satisfying the Second Law of Thermodynamics -- more than compensates for the decrease of entropy there where the crystalline phase appears.
H also means that the entropy of the surroundings will increase, and -- satisfying the Second Law of Thermodynamics -- more than compensates for the decrease of entropy there where the crystalline phase appears.
 G =
G =  H - T
H - T S for state transition : crystalline phase ==> aquous solution (sodium-sulfate decahydrate). See, to begin with, next Figure.
S for state transition : crystalline phase ==> aquous solution (sodium-sulfate decahydrate). See, to begin with, next Figure.
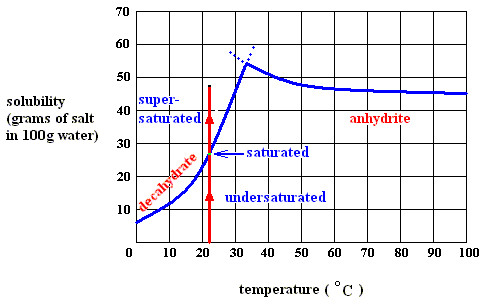
Figure above : Dissolution, saturation, and supersaturation (in water) of the decahydrate of sodium sulfate, at a temperature below 32.60C.
As long as the solution of the decahydrate is undersaturated, the dissolution process will continue (if enough material is available in the system). Heat is absorbed (according to the solubility curve of the decahydrate),  H is positive, but the entropy term more than compensates this, because the solution (which is a mixture) has a much higher entropy than the pure substances (solute and solvent) being separated from each other, so the change of (Gibbs) free energy for dissolution feasibility is negative (and thus making dissolution possible). Here the absorption of heat together with the increase of entropy of the system makes up the potential-energy surplus (potential-energy stock) as soon as the solution becomes supersaturated.
H is positive, but the entropy term more than compensates this, because the solution (which is a mixture) has a much higher entropy than the pure substances (solute and solvent) being separated from each other, so the change of (Gibbs) free energy for dissolution feasibility is negative (and thus making dissolution possible). Here the absorption of heat together with the increase of entropy of the system makes up the potential-energy surplus (potential-energy stock) as soon as the solution becomes supersaturated.
Although heat is absorbed (  H positive) in (and in virtue of) the dissolution process, and the entropy of the surroundings must, therefore, decrease, for the system the entropy increases, and according to the Second Law of Thermodynamics the latter must be such that the net overall entropy increases.
H positive) in (and in virtue of) the dissolution process, and the entropy of the surroundings must, therefore, decrease, for the system the entropy increases, and according to the Second Law of Thermodynamics the latter must be such that the net overall entropy increases.
 G =
G =  H - T
H - T S for state transition : aquous solution ==> crystalline phase (decahydrate).
S for state transition : aquous solution ==> crystalline phase (decahydrate).
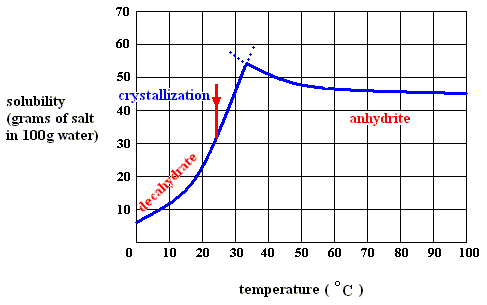
Figure above : Crystallization (from water) of the decahydrate of sodium sulfate, at a temperature below 32.60C.
As long as the solution is supersaturated (and initially crystallization nuclei being present), crystallization of the decahydrate continues (at a temperature below 32.60C ). Heat is being released,  H is negative. So the enthalpy term already contributes to making the (Gibbs) free energy difference
H is negative. So the enthalpy term already contributes to making the (Gibbs) free energy difference  G for crystallization feasibility negative, and more than compensates for the decrease in entropy of that part of the solution where crystals are formed ( T
G for crystallization feasibility negative, and more than compensates for the decrease in entropy of that part of the solution where crystals are formed ( T S negative). So also here the crystallization process is exothermal. It uses the (above mentioned) potential-energy stock of the solution.
S negative). So also here the crystallization process is exothermal. It uses the (above mentioned) potential-energy stock of the solution.
The negativity of  H also means that the entropy of the surroundings will increase, and -- satisfying the Second Law of Thermodynamics -- more than compensates for the decrease of entropy there where the crystalline phase appears.
H also means that the entropy of the surroundings will increase, and -- satisfying the Second Law of Thermodynamics -- more than compensates for the decrease of entropy there where the crystalline phase appears.
 G =
G =  H - T
H - T S for state transition : crystalline phase ==> aquous solution (sodium-sulfate anhydrite).
S for state transition : crystalline phase ==> aquous solution (sodium-sulfate anhydrite).
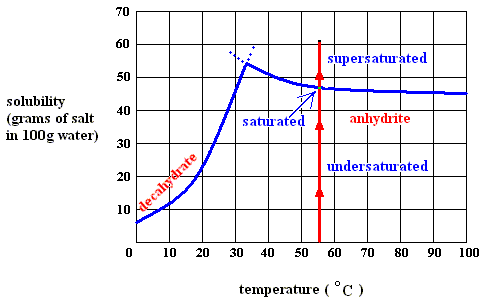
Figure above : Dissolution, saturation, and supersaturation (in water) of the anhydrite of sodium sulfate, at a temperature above 32.60C.
As long as the solution is undersaturated, the dissolution process will continue (if enough material is available in the system). According to the solubility curve of the anhydrite heat is evolved,  H is negative. T
H is negative. T S is positive.
S is positive.
As has been said, heat is evolved. It is dissipated into the environment and cannot be retrieved. So when dissolution (of dry sodium sulfate) is still going on, no energy is in fact stored in the system (as latent heat). The high potential energy of the initially unmixed solute-solvent system (dry sodium sulfate and water) decreases ( G negative) upon dissolution. Therefore, in the present case, dissolution proceeds spontaneously even when no heat were available to take in (
G negative) upon dissolution. Therefore, in the present case, dissolution proceeds spontaneously even when no heat were available to take in (  H is negative). Heat release, however, slows down the dissolution of dry sodium sulfate, because the temperature of the solution increases, and then the solubility of the anhydrite decreases. So in order to continue dissolution, the released heat must constantly be removed from the site of dissolution (just as, reversely, heat must be supplied to the site of dissolution in the case of potassium chloride, and also in the case of the decahydrate of sodium sulfate).
H is negative). Heat release, however, slows down the dissolution of dry sodium sulfate, because the temperature of the solution increases, and then the solubility of the anhydrite decreases. So in order to continue dissolution, the released heat must constantly be removed from the site of dissolution (just as, reversely, heat must be supplied to the site of dissolution in the case of potassium chloride, and also in the case of the decahydrate of sodium sulfate).
Although -- when dissolving anhydrite in water of above 32.60C -- heat is evolved when going from undersaturated to saturated, this cannot -- according to me [see below] -- be the case anymore when continuing from saturated to supersaturated (otherwise supersaturation of the solution would be a spontaneous process [if enough solute available] which it clearly is not). So upon supersaturation of the anhydrite in water (above 32.60C ) heat must be absorbed. And it is this heat which is released again upon crystallization. It, together with the increase of entropy of the system, constitutes the potential-energy stock of the (supersaturated) solution.
While in all endothermal dissolution processes heat is absorbed all the way from undersaturated to supersaturated, in exothermal dissolution processes (such as that of our anhydrite) heat is only absorbed from the saturated condition onwards (to the supersaturated condition).
The latter case (exothermal dissolution) can be elucidated a little more : If we go from saturated (solution of) anhydrite to supersaturated, we initially have (still) solid anhydrite present in a saturated solution (above 32.60C ) , that is, saturated with respect to anhydrite. Upon dissolution, and also upon supersaturation, the entropy term T S is favorable : a solution has a higher entropy than that of the solid state (that is, the state of solute and solvent being separated). But because a solution-becoming-supersaturated (further dissolution of the solid into the already saturated solution) is not a spontaneous process, the enthalpy term
S is favorable : a solution has a higher entropy than that of the solid state (that is, the state of solute and solvent being separated). But because a solution-becoming-supersaturated (further dissolution of the solid into the already saturated solution) is not a spontaneous process, the enthalpy term  H should clearly be unfavorable, that is,
H should clearly be unfavorable, that is,  H must be positive, which means that heat is absorbed. This heat is used to destroy the crystal lattice, that is, to randomize the particles of the crystalline residue still remaining in the saturated solution, and stored as potential energy. So, while dissolving sodium-sulfate anhydrite up to saturation is exothermal, continued dissolution (making the solution supersaturated) must be endothermal. As such this stored heat contributes to the potential energy-stock.
H must be positive, which means that heat is absorbed. This heat is used to destroy the crystal lattice, that is, to randomize the particles of the crystalline residue still remaining in the saturated solution, and stored as potential energy. So, while dissolving sodium-sulfate anhydrite up to saturation is exothermal, continued dissolution (making the solution supersaturated) must be endothermal. As such this stored heat contributes to the potential energy-stock.
In the present case heat is at first released (undersaturation ==> saturation), after which some heat is absorbed (saturation ==> supersaturation). This changes the entropy of the surrouindings. The entropy of the system increases. And according to the Second Law of Thermodynamics these changes must be such that the net overall entropy increases.
 G =
G =  H - T
H - T S for state transition : aquous solution ==> crystalline phase (anhydrite).
S for state transition : aquous solution ==> crystalline phase (anhydrite).
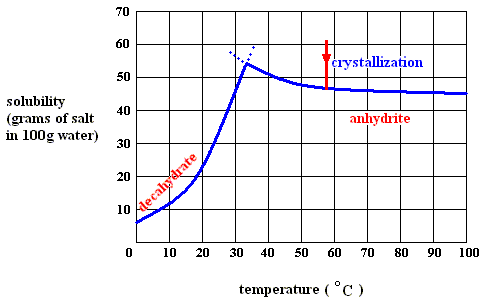
Figure above : Crystallization (from water) of the anhydrite of sodium sulfate, at a temperature above 32.60C.
As long as the solution is supersaturated (and initially crystallization nuclei being present), crystallization of the anhydrite continues (at a temperature above 32.60C ).
Upon supersaturating the solution of the anhydrite (at a temperature above 32.60C ), heat is absorbed (as explained above). Upon crystallization of the anhydrite this heat is released again, having  H negative. And because the entropy of the system decreases, T
H negative. And because the entropy of the system decreases, T S is negative, as such contributing to the positivity of
S is negative, as such contributing to the positivity of  G (that is unfavorable for the process at issue). But because crystallization of the anhydrite actually takes place (that is, it is regularly observed to take place under the conditions of supersaturation, temperature above 32.60C, and the presence of suitable crystallization nuclei), we must assume that the negativity of
G (that is unfavorable for the process at issue). But because crystallization of the anhydrite actually takes place (that is, it is regularly observed to take place under the conditions of supersaturation, temperature above 32.60C, and the presence of suitable crystallization nuclei), we must assume that the negativity of  H also in the present case more than compensates for the unfavorable entropy term T
H also in the present case more than compensates for the unfavorable entropy term T S .
S .
So also here the crystallization process is exothermal. It uses the (above mentioned) potential-energy stock of the (supersaturated) solution.
The negativity of  H also means that the entropy of the surroundings will increase, and -- satisfying the Second Law of Thermodynamics -- more than compensates for the decrease of entropy, there where the crystalline phase appears.
H also means that the entropy of the surroundings will increase, and -- satisfying the Second Law of Thermodynamics -- more than compensates for the decrease of entropy, there where the crystalline phase appears.
 G =
G =  H - T
H - T S for state transition : gaseous phase ==> gaseous solution (gas, vapor [water-vapor, air] ).
S for state transition : gaseous phase ==> gaseous solution (gas, vapor [water-vapor, air] ). H is positive, but the entropy term more than compensates this, because a solution has a much higher entropy than the solvent and solute in a separated condition ( which we can see as a ' hyper-undersatuated solution' ). So
H is positive, but the entropy term more than compensates this, because a solution has a much higher entropy than the solvent and solute in a separated condition ( which we can see as a ' hyper-undersatuated solution' ). So  G for dissolution feasibility is negative (meaning that dissolution is possible [under conditions of undersaturation] ). And as long as the air is undersaturated, the dissolution will continue, provided that material (water) continues to be available. Here the absorption of heat together with the increase of entropy make up the potential-energy surplus (potential-energy stock) as soon as the solution becomes supersaturated.
G for dissolution feasibility is negative (meaning that dissolution is possible [under conditions of undersaturation] ). And as long as the air is undersaturated, the dissolution will continue, provided that material (water) continues to be available. Here the absorption of heat together with the increase of entropy make up the potential-energy surplus (potential-energy stock) as soon as the solution becomes supersaturated. H positive) because of the dissolution process, and the entropy of the surroundings must, therefore, decrease, for the system the entropy increases, and according to the Second Law of Thermodynamics the latter must be such that the net overall entropy increases.
H positive) because of the dissolution process, and the entropy of the surroundings must, therefore, decrease, for the system the entropy increases, and according to the Second Law of Thermodynamics the latter must be such that the net overall entropy increases.
 G =
G =  H - T
H - T S for state transition : gaseous solution ==> crystalline phase (snow).
S for state transition : gaseous solution ==> crystalline phase (snow). H is negative, and as such contributes to the negativity of
H is negative, and as such contributes to the negativity of  G for crystallization feasibility, and, when the temperature is sufficiently low, more than compensates for the decrease of entropy there where the crystalline phase is formed. This decrease of entropy of the product of crystallization, as compared with the initial solution, causes
G for crystallization feasibility, and, when the temperature is sufficiently low, more than compensates for the decrease of entropy there where the crystalline phase is formed. This decrease of entropy of the product of crystallization, as compared with the initial solution, causes  S to be negative and thus causing the term T(
S to be negative and thus causing the term T(  S ) to be negative (because the absolute temperature is positive in every process). And by subtracting this negative term from
S ) to be negative (because the absolute temperature is positive in every process). And by subtracting this negative term from  H works against
H works against  G to become negative. But because T is low (supposed to be below 00C ) the negativity of the term T(
G to become negative. But because T is low (supposed to be below 00C ) the negativity of the term T(  S ) is not very significant, as is then also (not very significant) its contribution to the positivity of
S ) is not very significant, as is then also (not very significant) its contribution to the positivity of  G . And because (in the presence of suitable crystallization nuclei) such an undercooled solution indeed is observed to give rise to crystal formation, we know that the degree of negativity of
G . And because (in the presence of suitable crystallization nuclei) such an undercooled solution indeed is observed to give rise to crystal formation, we know that the degree of negativity of  H more than counterbalances the just mentioned (insignificant) contribution to positivity. So
H more than counterbalances the just mentioned (insignificant) contribution to positivity. So  G (for crystallization feasibility) will be negative, implying that crystallization is possible under the mentioned circumstances.
G (for crystallization feasibility) will be negative, implying that crystallization is possible under the mentioned circumstances.  H being negative, means that also in the present case the crystallization process is exothermal. It uses the potential-energy stock of the solution.
H being negative, means that also in the present case the crystallization process is exothermal. It uses the potential-energy stock of the solution. H also means that the entropy of the surroundings will increase, and -- satisfying the Second Law of Thermodynamics -- more than compensates for the decrease of entropy, there where the crystalline phase appears.
H also means that the entropy of the surroundings will increase, and -- satisfying the Second Law of Thermodynamics -- more than compensates for the decrease of entropy, there where the crystalline phase appears.
Let us now give a more compact (and therefore more surveyable) account of the above list, concentrating on origin and expenditure of the potential-energy stock with respect to the form-generating process (crystallization), and the entropy changes of the system and its surroundings.
 H (change in enthalpy) in
H (change in enthalpy) in  G =
G =  H - T
H - T S , relates to the stabilities of initial and final states, and, therefore, to heat absorption or heat release effecting a change in entropy of the surroundings (of the system-proper).
S , relates to the stabilities of initial and final states, and, therefore, to heat absorption or heat release effecting a change in entropy of the surroundings (of the system-proper). S relates to the change in entropy (
S relates to the change in entropy (  S ) of the system (that is, it relates to the difference in entropy between initial and final state of the system).
S ) of the system (that is, it relates to the difference in entropy between initial and final state of the system). H positive) and transformed into potential energy.
H positive) and transformed into potential energy.
 S positive).
S positive).
 H positive).
H positive).
 H is negative.
H is negative.
 S negative).
S negative).
 H negative).
H negative).
 H positive) and transformed into potential energy.
H positive) and transformed into potential energy.
 S positive).
S positive).
 H positive).
H positive).
 H is negative.
H is negative.
 S negative).
S negative).
 H negative).
H negative).
 H positive.
H positive.
 S positive.
S positive.
 H positive).
H positive).
 H is negative.
H is negative.
 S negative).
S negative).
 H negative).
H negative).
 S positive.
S positive.
 H negative for the crystallization process.
H negative for the crystallization process.
 S negative.
S negative.
 H negative).
H negative).
 H positive) and transformed into potential energy.
H positive) and transformed into potential energy.
 S positive).
S positive).
 H positive).
H positive).
 H negative).
H negative).
 S negative).
S negative).
 H negative).
H negative).
With the above lists I hope to have thermodynamically elucidated the process of crystallization from a melt, from a liquid solution, and from a gaseous solution.
which is perfectly comparable to the falling stone and its non-elastic impact.
So crystal growth is (ultimately) an exothermal process, whose potential energy is represented by the disordered configuration of nutrient particles (in the solution or in the melt), that during melting (or [in many cases of] dissolution) had gained surface energy at the expense of heat ( PRZIBRAM, Ibid., p.113).
Indeed, every real-world process is a series of energy transformations and energy conduction or flux, which latter is in fact energy discharge.
For a process to get started and to be maintained, the conditions must first of all be such that an energy flux through the system is made possible. With this we enter into a consideration of energy kinetics, that is, we now turn to the process as it unfolds in time.
General Context of Investigation.
Entering a consideration of the form potential, especially of branched crystals, it is perhaps useful to remind the reader of the context we're in. This context is an investigation of Categories of Being of the Inorganic Layer of Being, such as Process, Causality and the like, and see whether, and if so, in what way, they are found again in the Organic Layer. Especially, investigating the nature of causality demanded a thorough thermodynamic treatment of processes, because processes consist of states that are causally connected and are in fact a series of energy conversions. We ended up with a thermodynamic understanding of inorganic processes in general, and with it with an understanding of the nature of causality as it manifests itself in the Inorganic Category Layer of Being. In order to understand how the Inorganic Layer relates to the Organic Layer, we must see what the general character is of processes in the Organic Layer, that is, we must investigate the relevant categories in that Layer. And we have proposed to do this by means of a crystal analogy. By collecting features (morphological, thermodynamical, physiological, etc.) that are similar (that is, that are more or less commonly possessed) in crystals and organism, we can perhaps discover a general common ground for organisms and crystals which permits us to judge the nature of the stock of organic categories (as compared to the stock of inorganic categories). We have already found out a certain type of crystals that is most suited to play a major role in the crystal analogy : dendritic (that is, branched) crystals, exemplified in certain snow crystals and in windowpane frost. On inspection they turn out to have an enormous morphological potential. And this is relevant and important because one of the greatest problems in organic development is the origin and maintenance of the general macroscopic morphological lay-out of a given organismic body, or, more generally its vectorial nature. We could make a beginning to understand this by seeing the organismic body being underlied by some sort of lattice or organic crystal, which, by controlled fast growth generates the general morphological lay-out of the body of some given organism. This is the Theory of Organic Lattices, which we have developed in Part XXIX Sequel-10, Sequel-11, and Sequel-12.
However, to postulate an underlying lattice structure within an organismic body could create as many and serious problems as those for whose solution it was meant to serve. A materialized lattice is a rigid structure (as it indeed is in crystals [in liquid crystals there are no genuine lattices, but only some one preferred direction of orientation of constituent particles] ), while an organismic body generally is not.
When particles have settled into their lowest-energy positions, then the resulting physical body is more or less rigid. And also when they are held away from these positions, and thus settle for a bit higher than lowest-energy positions, the resulting physical body is still more or less rigid. Indeed genuine crystals are rigid bodies. Their particles have settled for lowest-energy positions (even if that means that they have moved farther apart, as it is the case in the freezing of liquid water).
Organisms, on the other hand, are not rigid bodies (although they often contain rigid substructures such as skeletons or shells). The softness of organisms is an expression of their general state of aggregation : they are semi-liquid. Generally, a fluid state of aggregation (semi-liquid, liquid, gaseous) means that the particles of the body, that is in this state of aggregation, have more freedom to move (around) than they have in a solid body, such as a crystal, where they can only vibrate about average but definite positions, resulting in the fact that the internal microscopic structure of these rigid bodies is maintained.
As we know, in organisms the constituent microscopic particles generally can move freely over more or less macroscopic distances (while the organs of organisms generally have fixed positions). So an organic lattice (resulting, as in crystals, from energetic relations between particles) cannot, it seems, be rigid, because in that case the whole organismic body would be rigid, which it clearly is not. But when such a lattice is not rigid, its constituent particles are more or less free to move (over [at least small] macroscopic distances), which means that it is not a lattice at all. So if we want to postulate a lattice of some kind in organismic bodies, in order to account for the organism's general morphological lay-out, or more generally, to account for its definite vectoriality, this organic lattice must be of a very special nature (perhaps as a result of the categorical NOVUM presumed to be present in the Organic Layer, as considered in earlier documents) : It must be rigid, while at the same time the organismic body being not rigid. In our Theory of Organic Lattices we postulated that such a lattice must be litterally flexible (that is, it can be bent and folded). This was in order to account for the folded condition of immature stages (in organisms) in many cases, and to account for the flexible nature of organismic bodies anyway : These bodies can bend, twist and curve themselves in diverse ways. For flexible and deformable lattices we assumed that, while deforming, their symmetry relations are nevertheless preserved, although from a purely geometric perspective they are not preserved upon deformation.
Now we could call the preservation of the symmetry relations of such lattices upon deformation -- their "r i g i d i t y".
These symmetry relations (mirror symmetry, rotational symmetry, translational symmetry, etc.) cannot, therefore, be purely geometric, but must also be more or less physiological : Upon geometric deformation of the organic lattice, its symmetry relations are, physiologically, preserved. So in this way we have a rigid lattice structure within a non-rigid organismic body. The organic lattice, therefore, is not strictly geometric, it is physiological as well. And this 'rigid' organic lattice can grow like a crystal by apposition of units onto its exterior, units which can, after the fact, be recognized as unit cells in the crystallographic sense. The next series of Figures illustrate the deformation of a (two-dimensional) lattice, and indicates the preservation of its intrinsic symmetries.
Figure above :
Top image : A two-dimensional square lattice. As such it has P4mm plane group symmetry, and 4mm point group symmetry. It has this same symmetry when provided with motifs (arranged according to this lattice) that have 4mm symmetry, that is, possesing a 4-fold rotation axis and two types of mirror lines.
Bottom image : This same lattice, but now (geometrically) distorted (by some topological transformation, that is a transformation without involving ruptures). Upon distortion, the number of meshes remains the same, as well as the number of corners (4) of each mesh. The angles, however, change.
The next Figures indicate the preservation, upon the above distortion, of the symmetries inherent in the square lattice, that is, the symmetries are preserved in a chemical or physiological sense.
Figure above : Same lattice, same distortion.
Mirror symmetry is chemically preserved, despite geometric distortion. One such mirror line (representing one of the two types) is highlighted in both images (red line).
Figure above : Same lattice, same distortion.
Mirror symmetry is chemically preserved, despite geometric distortion. One such mirror line (representing the other of the two types) is highlighted in both images (red line).
Figure above : Same lattice, same distortion.
Rotational symmetry is chemically preserved, despite geometric distortion. The 4-fold rotation axis is shown in both images.
In the case of a deformed organic lattice, not only its geometrical symmetries are destroyed, but, in principle also the corresponding chemical symmetries, because of a change in mutual distance and proximity of chemical units (influencing the nature of possible chemical reactions). So we assume that in the organism these chemical consequences are in some way neutralized (by compensation reactions), restoring the chemical symmetries.
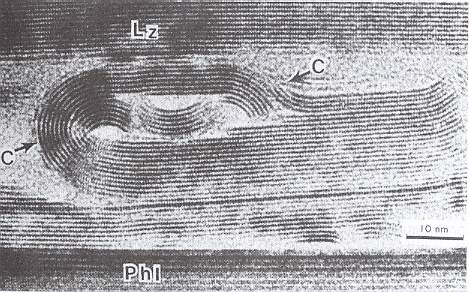
Figure above : HRTEM structure image of locally deformed (curled) serpentine (C) inside a matrix of well-layered lizardite (Lz), also a variety of serpentine. The curled region occurs along a cleavage fracture. Phl = phlogopite mica. Scale is in nanometers.
(After KLEIN & HURLBUT, 1999)
Bended structures are also encountered in snow crystals, for example the bended ridges of certain sectored plates (See Figure below ), but here there is no bending of the crystal lattice ( LIBBRECHT, K., The Snowflake, 2003, p.72).
Of course it could be that organisms do not possess an organic lattice in whatever from at all. Their morphological lay-out is then the result of some other process (for instance ' Turing structures ' ), not related to crystallization. But it could also be that organisms, in their very early stages of evolution did have their general morphological lay-out accomplished by a process similar to crystallization. This process was, however, discarded in later evolutionary stages and replaced by some more sophisticated (and more controllable) process of form generation. The initial crystallization-like process has, seen after the fact, served as a sort of scaffold for the development of the more sophisticated process. After the latter had been (phylogenetically) firmly established, its scaffold was no longer needed, and was disposed of. And because the sophisticated form-generating process was built out of the scaffold, that is, out of the crystallization-like process, it is no wonder why all organisms we know of (still) show many analogies with crystals.
It this is correct, the crystal analogy, that we are working out already for some time, is still relevant, even when all organisms of which we can study their internal organization and individual development do not possess an organic lattice (anymore).
Once given the (individually) incipient organic lattice (as a 'crystal seed'), the general morphological lay-out of the organismic body is then generated by the (controlled) fast growth of this organic lattice, resulting in a complex dendritic organic crystal. And this is the reason why we go so deeply into the generation, and internal and external structure, of dendritic crystals. Therefore we begin with, what is called, their form-potential difference.
The Form-Potential Difference Field or Vector Rosette of Actual Growth in crystallization.
For a process to get started and to be maintained, the conditions must first of all be such that an energy flux through the system is made possible.
When could we expect a flow or flux of energy to set in?
If we have a closed system, say some physical body, that is insulated from the outside world with respect to a given energy form, resulting in the fact that this energy form cannot leave or enter the system or physical body, then no reason for a change in the energy state is given. The quantity of actual energy present at the surface of the physical body will, in virtue of progressive extension, have reached a state of equilibrium, and when there is a source of energy of the same quality in the center of the body, then the overall effect at the surface can only consist in a gradual increase of energy intensity. Do we thus have a body that is thermally insulated from the outside world, and that possesses a heat source in its center, then the temperature of its surface will increase. Now when one --with regard to the just given example -- lets another body approach this surface -- all the way through the insulation layer -- a body that can absorb heat energy, then we have the situation for which the following rule (in fact the Second Law of Thermodynamics) holds : Between two sites possessing an unequal power to effect something, that is, possessing an unequal amount of the same energy form or (an unequal amount of) 'charge', there will develop an equilibrium (that is, a leveling-out) as a result of energy flux. The rate of this flux is proportional to the difference in energy intensities that are about to be leveled out, and should, therefore, ceteris paribus, and when only a given amount of energy stock is available, be inversely proportional to elapsed time (because the mentioned difference dwindles with time). So the deduction of energy from a source will proceed faster the greater this difference is between the source and the 'well'. Because the capacity to receive the energy depends on the magnitude of the area of the interface between supplying body and receiving body, and on the special and relevant properties of the bodies and their substances (heat capacity, electrical capacity, etc.), so also the rate of the energy flow will increase upon an increase of interfacial area and upon an improvement of the mentioned relevant properties of the materials, and will influence the effects that manifest themselves along the way of this energy flow. Favorable for a deduction (that is, discharge) of energy and for sustaining a constant flow or flux of it from some given source, are, consequently such system conditions that bring about an increase of relative surface area, that is, the magnitude of interfacial area per unit volume, or the use of a better conductor for the travelling energy. If under otherwise the same conditions, and thanks to the existence of the potential difference, a continuous flow of energy exists from an energy source, residing in the center of the body, to the up-to-now still poorer supplied surface, then we always have the possibility, to enforce an energy discharge as a result of attachment (that is, a contact) of a second body made up of the same substance, provided this body is in a state that makes it accessible for the energy form concerned. In the case of a body of a different make-up (for example consisting of a chemically different substance, different from the body to which it is attached), it will depend on its capacity in relation to that of the source system (the body to which the second body is brought into contact). In the same way a specific state of the substance will be favorable for the initiation and maintenance of the energy flow, namely the complete discharge of the energy (form) to be received. A body, impoverished with respect to a given energy form (quality) must effect an acceleration (according to the relative surface areas) of the discharge of qualitatively the same energy, when it is brought into contact with a charged body of the same sort (that is a body having this energy form in a larger quantity). A different body can (depending on its specific properties) possibly do this also, but that cannot be predicted just like that.
Let us now apply these findings about energy discharge to the situation as it is in crystallization. There we have a 'body' possessing a stock of energy of some form, which body is the solution or melt. In addition to that we have a second body that can receive this energy, that is, a body that represents an energy 'well' with respect to the energy form or quality concerned. This latter body is a crystal embryo or (macroscopic) crystal fragment of the same substance that is dissolved or that is molten.
Because a crystal, as a fragment, added to a supersaturated solution or undercooled melt, is with respect to its potential energy a discharged phase of its nutrient environment (solution, melt), it must represent a well for the potential energy of the nutrient material, and the crystal gets growing as soon as it can overcome the surface-tension pressure (which is an effect of the intensity factor [surface tension] of the potential energy [surface energy of the first sort] ). With the crystal fragment being a well, energy is then released. In fact the energy is released not from the crystal fragment itself (from where energy had already been released earlier), but from precisely that part of the solution or melt in the immediate vicinity of the crystal fragment that is about to solidify.
All this is just like a lifted stone : The stone possesses potential energy (because of having been lifted up), and the ground represents a well with respect to this potential energy. When the stone is released, we get a discharge of energy, that is, a flow of energy from the level of high potential energy (height from which the stone is released) to the lower level of potential energy (ground). The potential energy is carried by the stone while this energy is progressively being converted into bulk kinetic energy, till the stone hits the ground, where the energy is -- in the supposed case of inelastic impact -- again converted, now into heat, which is released.
The impoverishment with respect to potential energy (surface energy of the first sort) evokes, according to the difference in potential energy, crystallization by engrafting the solution or melt with a crystal fragment (of the same substance as the solute or melt).
A crystal fragment of the same substance as that of the solute or melt must -- under the condition of supersaturation or undercooling -- prime the crystallization process, while a crystal of a different substance or some non-crystalline body could possibly do it, depending on the relations of potential energy that it entails.
But while the crystal itself, as it shoots up from its nutrient medium (solution, melt), creates the energy flux, because it, as impoverished phase of the same substance, eases the discharge of energy, its growth at the same time changes the surface area in a non-favorable way. The surface area (that is, crystal interface) increases, causing the linear growth (growth as seen along some given direction) to slow down. And, the other way around, damage inflicted to a crystal (for instance by truncating one of its corners [and then letting the crystal grow again] ) increases the surface area with respect to the involved part of the surrounding solution or melt and so eases the discharge of energy, resulting in a fast deposition of material at the site of damage.
We can ascribe to the nutrient medium (solution, melt) a Form-Potential Difference Field as soon as it contains a crystal seed or embryo, a potential that, going out from the seed center, has a different magnitude in different directions, and uniformly decreases with increasing distance from that center.
It is necessary to explain this form-potential difference field, especially its decrease with distance from the center of the crystal seed :
What we have discussed so far (i.e. until now) is the feasibility of the transition from the liquid (or, generally, fluid) phase (solution, melt) to the solid phase in terms of general thermodynamics. And when a crystal embryo (which can be formed just by chance) happens to be of sufficient volume, it can overcome that surface energy that consists of the presence of non-satisfied or distorted chemical bonds at the surface of the crystal embryo, and the crystallization process actually gets going.
Now, when the crystallization is finally under way, we must consider the shape that the growing crystal actually and finally adopts.
As has been said, the sufficiently sized crystal embryo is an energy well for the (higher) potential energy of the supersaturated solution or the undercooled melt. This sets up an energy flow toward this well (that is that part of the solution or melt that is about to solidify, i.e. which is the incipient crystal adjacent to the crystal seed in the sense of its natural extension by growth), which (flow) consists in the 'falling' into position (lattice point position) of the particles. This means crystal growth, and as such represents outward pressure. Now, a crystal in the solution or melt has a surface, and having a surface (interface) carries an energy cost : At the surface of a (growing) crystal the particles of the crystal cannot experience as many attractive, stabilizing interactions with neighbors as do particles in the bulk of the crystal, and so the surface particles have a high energy relative to the bulk. The larger the surface area, the greater the energy cost. We generally speak of this excess energy as the surface tension (surface energy of the second sort), since its effect is to pull the crystal into a compact form (as is directly evident in the case of liquids, that is, liquid drops), keeping the surface area as small as possible.
If the crystal were just slavishly following this surface tension (as we see in liquid isotropic bodies such as water droplets), it would deform into a sphere because a sphere has the least relative surface area (relative to its volume). But solid crystals are not developing into spheres but into polyhedrons, that is, into bodies bounded by (generally) flat faces. So there must exist forces that -- in a differentiated way -- go against the surface tension (that is, against the inwardly directed pressure entailed by it).
Indeed, the growth of a crystal is nothing else than (or at least equivalent to) a force directed outward (that is, a growth force). And because a crystal is intrinsically anisotropic -- that is, it has different properties in different directions -- its growth forces must be different in different directions. In fact there are sets of directions (where sometimes a set consists of only one direction), each set consisting of (a set of) equivalent directions corresponding to equal growth rates and thus to equal outwardly directed pressures, while these sets are different from each other in this respect, and thus entailing different growth rates and therefore different outwardly directed pressures. These differences, as they depend on direction, are entailed by corresponding differences in atomic aspects of the crystal faces as they present themselves to the nutrient environment. So in a growing crystal the overall surface-tension pressure (which causes spherical forms in isotropic bodies) is opposed by sets of outwardly directed growth pressures whose magnitude is dependent on the direction. And that is why crystals do not develop into spheres. And because there is no essential deformation of a fully developed crystal in a saturated solution (to stick to the example of crystallization from a solution), the surface-tension pressures must be balanced by the directional growth forces, at all points on the crystal surface.
Where we have a corner or edge of the crystal, the growth force or pressure is intrinsically higher than that of the surroundings (on the crystal surface) of the corner or edge, which higher pressure has caused the bulging (or bending) of the crystal surface (having resulted in the corner or edge), and this bulging in turn evokes an inwardly directed surface-tension pressure, increasing as the radius of curvature decreases, that is when the bulge becomes sharper and more pronounced : For example, if we stretch an elastic band, it tries to contract again (by evoking a restoring force [and this latter stands for surface tension] ), and when we do this over a curved surface the restoring force of the elastic band causes a pressure downwards (or inwards for that matter) as the next Figure illustrates :
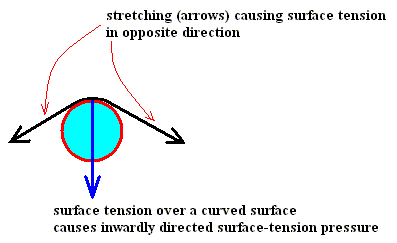
which (surface-tension pressure) now counteracts, and finally balances with the growth pressure. So the fully developed crystal represents a state of equilibrium between the growth pressures and the surface-tension pressures.
When we now remove an arbitrary part of the crystal, say, by truncating a corner, this equilibrium must become disturbed as a result. And the return to equilibrium can only take place when the surface-tension resistance, evoked by the renewed growth at the site of damage, will finally stand in the same relation to the restored shape again, as it was before the removal. And because at all non-damaged sites of the crystal equilibrium was not disturbed, we can now conclude that the site of damage has experienced a preferred increase of mass. In other words, when we have a crystal, and see how the growth rate differs with the distance from the crystal center, we find, through truncating a corner, which amounts to exploring the interior of the crystal, that growth intrinsically is faster at distances closer to the crystal's center, that is, linear growth (growth as seen along some direction) decreases with distance from that center.
The regeneration of a crystal (restoration of its intrinsic shape under given conditions) is a return to equilibrium in two respects :
One of the dynamic equilibrium between dissolution (or melting) and deposition, and one of the static equilibrium between surface-tension pressure and specific anisotropic directional (growth) force ( PRZIBRAM, Ibid., p.63). The latter equilibrium relates to the shape adopted by the crystal.
So now we have established that in a supersaturated solution (or undercooled melt) there is a Form-Potential Difference Field that is different for different directions, i.e. that is anisotropic, and that falls off with increasing distance from the center of the crystal (seed). And this form-potential difference field is equivalent to our Vector Rosette of Actual Growth as a set of (fast) molethynes, that was discussed in Part XXIX Sequel-15 .
Having considered the thermodynamics of crystallization as we see it in normal -- that is, not too fast-going -- crystallization, we must now turn to the formation of dendritic crystals, which is a case of very fast crystallization. Thereby we will especially concentrate on the dendritic ice crystals that form directly from water vapor in the air, that is, from a gaseous solution of water vapor in the air, as we see them in certain kinds of snow crystals and in windowpane frost. Much work on this subject has already been done on this website. We have discussed the formation of such crystals, mainly from a morphological point of view (Part XXIX Sequel-3, Part XXIX Sequel-6, Part XXIX Sequel-8, Part XXIX Sequel-15). Now we will discuss it from a thermodynamic viewpoint (which we already began in the previous document) and compare it with truly far-from-equilibrium thermodynamic systems such as the Bénard Instability (discussed earlier).
Probably the best way to assess the thermodynamic status of dendritic crystallization, taking as an example that of water vapor from the air, is to depart from the potential-energy discharge together with the fact of high supersaturation levels of water vapor with respect to ice. The most favorable temperatures for the dendritic ice crystals to evolve are around minus 150 C, because there the largest amount of water vapor per unit air volume can exist (as vapor) before this vapor turns into (macroscopic) droplets of liquid water (from which no snow crystals or windopane ice feathers will develop). So here the conditions are favorable for fast ice crystal growth.
Formation of a dendritic snow crystal from a thermodynamic viewpoint.
We will now assess whether the process that generates dendritic snow crystals (and therefore all processes that generate dendritic crystals) is a far-from-equilibrium thermodynamic process or not.

All natural snow crystals originate in the air, that is, in the earth's atmosphere.
Figure above : A two-dimensional snow crystal, based on a hexagonal net. Of course this net extends only as far as the crystal itself extends. The crystal, blue, is suppposed to be the initial (small) hexagonal plate, onto which further layers will be deposited (at conditions of slow growth), or from whose corners branches will grow out as a result of fast additional growth. The crystal is built up by the periodic stacking of rhomb-shaped building blocks (of which the chemical content is not depicted). Each (rhomb-shaped) building block geometrically consists of two equilateral triangles. The arrows indicate the growth directions of the six 'faces'.
Shown here is the (transverse) deposition of three new layers (red, brown, red) of rhombic building blocks (shown only for the top part of the crystal). As one can see, such a way of growing does not (significantly) increase the area of contact between charged phase (roughly : [gaseous] solution) and impoverished phase (roughly : surface of growing crystal).
The next figure compares this with repeated elongation of a layer, that is, not a stacking of layers on top of each other, but one layer being deposited as an extension of a previous one :
Figure above : Comparison of transverse deposition (top : red--brown-red) and lengthwise deposition (bottom-right : red--brown) of layers of rhomb-shaped building blocks, with respect to the concomitant increase of the area of contact. One can see that transverse deposition of layers increases the area of contact only slightly (if at all), while lengthwise deposition lets this area increase significantly.
The direction of the outgrowths (Figure above : bottom-right) coincides with a direction of fast growth, that is -- now considering the three-dimensional tabular snow crystal -- fast growth of a possible (second type of) prism (side-) face that has, because of its fast growth (in combination with tapering adjacent faces), grown itself out of existence (see next Figure), resulting in an edge (parallel to the c-axis, that is, to the main axis). And because edges stick out better into the ambient nutrient material (better than the central parts of faces), they will more easily pick up particles.
The next Figure recalls what "growing itself out of existence of a possible crystal face" means (here exemplified by the transformation of an initially octogonally shaped crystal into a tetragonally shaped crystal) :
Figure above ( = Figure 7 of Part IV) : Successive stages in growth of an imaginary two-dimensional crystal. Growing faster than the x-faces, the y-faces may finally disappear.
When a snow crystal grows rapidly, it develops outgrowths. Such outgrowths are likely to start off from edges or corners, because they can be supplied from more directions, in our case supplied by water molecules present in the air. But, as far as I can see from the many microphotographs taken from snowflakes, these outgrowths do not appear at the edges that separate the upper face, as well as the bottom face of the (flat) hexagonal prism, from its sides. The outgrowths appear to develop only at the edges separating the sides of the prism. See next Figure (Taken from Part XXIX Sequel-4 ).
Figure above : Diagram of a snowflake, with and without outgrowths.
The snowflake is depicted here as a hexagonal prism, which indeed it is. In reality, however, the prism is much more flattened in the case of branched snow crystals.
Image a : Hexagonal snowflake prism without outgrowths.
Image b : Hexagonal snowflake prism with outgrowths (one shown) at the vertical edges separating the sides of the prism, where they (i.e. the outgrowths) are indeed actually found.
Image c : Hexagonal snowflake prism with outgrowths (one shown) at the horizontal edges separating bottom and top face from the vertical sides. To my knowledge, such outgrowths (which are obliquely positioned with respect to the prism [basal] faces) are not found in snowflakes.
The formation of branched snow crystals must be seen in the following growing context :
Figure above ( = Figure 11 of Part IV) : Besides the chemical composition (chemical aspect presented to the environment) the growth rate of a face is inversely proportional to the number of lattice nodes that are encountered by that face.
The figure shows a primitive rectangular point net (The argument to come also applies to a 3-D point lattice). The intersections of the lines making up the rectangular cells (meshes) are lattice nodes (These nodes represent the locations of chemical units).
Four possible faces are indicated by a, b, c and d. The arrows indicate their respective directions of growth (At the same time there is also a corresponding growth in the opposite directions of the arrows). Generally the slowest growing faces become the most prominent faces on the crystal. The fastest growing faces quickly grow themselves out of existence.
This Figure -- which concerns the growth rates of faces -- only pays attention to one feature of the atomic aspect (The atomic aspect determines the growth rate of a face), namely the density of nodes encountered by the crystal face in question (The other feature refers to the chemical composition of the crystal).
The slowest growing face (on the basis of the feature mentioned) is face b, because here the density of nodes (encountered by that face) is highest.
Next comes face c, and then a.
The fastest growing face is d.
So the faces b and c will become the most prominent faces. The other faces will eventually grow themselves out of existence.
Because the faces b and c are perpendicular to each other the faster growing face of these two, namely c, will not grow itself out of existence. It keeps on growing, and keeps on growing faster than b, so the crystal will finally adopt a rectangular shape with its longest dimension oriented vertically.
The following Figures and text will explain branched crystals further, based on earlier investigations on this website ( Part XXIX Sequel-3, Part XXIX Sequel-15, Part XXIX Sequel-17 ).

The next Figure shows a hexagon-shaped snow crystal in which the effective molethynes are materialized in the form of ridges. It is a crystal that is one sectored plate.

Figure : Hexagonal sectored plates are small and uncommon. This tiny example is only 0.3 mm (0.01 inches) in size. We here have a hexagonal crystal with its six effective molethynes (lines of directional forces) materialized as ice ridges (three different directions + opposites). We assume that these materialized molethynes are in fact crystal faces, albeit very small faces, corresponding to the growth direction as indicated by the molethyne, or, in other words, such a materialized molethyne is a growth trail of the corresponding very small but fast growing crystal face.
(From Part XXIX Sequel-17)
(Photograph by Patricia RASMUSSEN, in The Snowflake, 2003, by Kenneth LIBBRECHT.)
I assume that a ridge in a sectored plate not only represents a direction of some fast growing possible crystal face, but that it also is that face itself, albeit a very small face, equal to the width of the ridge, as we see it also in the case of slender branches and side branches in stellar snow crystals. Because it is a fast growing 'face' it will not fully develop, because extension of its surface is denied by the two adjacent tapering slower growing faces. This 'face' has its (very small) surface of course perpendicular to the ridge, i.e. perpendicular to its growing direction.
The possible (fast growing) faces, seen in a projection of a snow crystal along its c-axis, are indicated in the next Figure. Although not developing into genuine crystal faces, they can develop into ridges and into their extensions : branches (with or without sectored plates).
Figure above : Fast growing possible faces of the crystal are indicated (red) together with their directions of growth (arrows), a, b, c (including their opposites). These directions will be materialized by branchings, when further growth of the crystal is (very) fast. These branches, and also their side-branches (standing off at 600) represent the effective molethynes of the snow crystal. As such the molethynes obviously determine the shape of a fast growing snow crystal. But they also determine the shape of the crystal (as seen in the mentioned projection) in the case of slow growth, i.e. they are also responsible for the hexagonal shape of plate-like snow crystals. In this case (of slow growth) the fast growing faces diminish gradually until they have vanished altogether and thus have been transformed into corners. (From Part XXIX Sequel-15)
Figure above : Small initial hexagon-shaped snow crystal (seen as a projection along the c-axis onto the plane of the hexagonal plate of the crystal). The generation of this crystal, that came into being by slow crystallization, is followed by fast growth, resulting in branches. The six primary branches (which here are depicted only as directions) representing growth directions of fast growing faces are indicated as dark blue lines going off from the six corners of the initial hexagonal plate. (See also previous Figure). The fast growing faces themselves do not develop (as faces). The three directions (including their opposites) are labelled a, b, c. (From Part XXIX Sequel-15)
The next Figure depicts, in addition to the primary branches, also secondary and teriairy branches.
Figure above : Same as previous Figure. Secondary and tertiary branches added (the latter are indicated as red lines and red labels). The secondary and tertiary branches show only the directions a, b and c, other directions do not occur among them. As in the previous Figure, the drawing only concentrates on the directions of the branches, not on their (relative) lengths, nor on their (internal) structure.
(From Part XXIX Sequel-15)
The 600 angles that the secondary branches make with the primary branches are made more evident in the next Figure.
Figure above : Formation of an outgrowth (blue) at a corner of a hexagonal crystalline plate (blue) in the context of crystal growth by increments. These increments, as representing possible crystal faces, are indicated by x, y, z, etc., and a, b, c, etc. The Figure is not meant to present a full explanation of the appearance and general morphology of an outgrowth, but is only meant to give some indications that could stimulate further pondering. It probably gives some hint why the angles that the side branches make with the outgrowth's main axis are all 60 degrees.
(From Part XXIX Sequel-3)
All these branches (primary, secondary, tertiary, etc.) represent, with their directions, the set of effective molethynes of the snow crystal, and of ice crystals in general.
For real snow crystals, humitity conditions during growth, at, say, - 150 C, can change from relatively low humidity (giving hexagonal plates without branches), to high humidity (branches appear at the corners of the initial hexagonal plate), and to low humidity again ( [short] faces [parallel to c-axis] develop between [side] branches, resulting in sectored plates [which look like fins] ).
The process, resulting in branched crystals, does, as long as it continues, not reach thermodynamic equilibrium. The resulting structure, the ice dendrite, remains an unstable structure. It is as if the flat hexagonal prism had been damaged in some way, that is, it is as if sectors of material had been removed, resulting in a disturbance of the balance between surface-tension pressures and (anisotropic) growth forces (intrinsic directional forces of growth of faces). And as long as this equilibrium is not restored, the structure is unstable. It is 'kept alive', so to say, by the enduring of the large potential energy fall (energy difference), which "enduring" means that there is no leveling-out of this fall. And at the same time the surface of contact between the charged phase and the impoverished phase is increasing ever more, and so accomodating better and better to the large energy fall (to be equalized), that is, providing an ever better passage way for the energy discharge. But upon the crystal becoming more and more 'spiky', its surface energy (caused by unsatisfied chemical bonds) increases, while the increase of its volume lags behind. So the process cannot go on indefinitely. Further growth of branches will increasingly be replaced by the growth of (localized) facets, resulting in a strong increase of crystal volume again (locally, layers of building blocks are now deposited on top of each other, resulting in sectored plates or related structures). At the same time there is now a reduction of the increase of surface area.
Dendritic crystallization as a non-linear far-from-equilibrium thermodynamic process : The Branching Instability.
Let us summarize our insight, so far, of the formation of dendritic crystals, focussing on dendritic ice crystals from water vapor in the air.
We start with an ambient temperature round about minus 150C and low humidity, but a humidity which already represents a supersaturation of the air with water vapor, a supersaturation with respect to ice. In such a medium, which is a (gaseous) solution of water vapor in air, and which is only metastable as to its state of aggregation, microscopically small patches of water molecules, ordered according to the hexagonal space lattice of ice, occasionally form by chance, or, stimulated to order in that way by dust particles or by microscopically small frozen water droplets (ice pellets). We can interpret such chance formations as fluctuations occurring in the metastable (that is, unstable but not yet kicked to the stable state) medium ( = supersaturated [with respect to ice] solution of water vapor in the air at about minus 150C ).
If such a microscopic patch of hexagonally ordered water molecules happen to exceed a critical size, that is, if such a fluctuation becomes large enough, growth of it will entail a decrease of the Gibbs free energy ( G ), that is, the surface energy (
G ), that is, the surface energy ( Gs ), caused by dangling chemical bonds, will be overcome, and the patch (crystal embryo) will indeed grow spontaneously. And under the mentioned conditions (low humidity, that is, low supersaturation with respect to ice, and a temperature of about minus 150C ) the ice crystal will adopt the shape of a thin hexagonal plate, that grows larger and larger.
Gs ), caused by dangling chemical bonds, will be overcome, and the patch (crystal embryo) will indeed grow spontaneously. And under the mentioned conditions (low humidity, that is, low supersaturation with respect to ice, and a temperature of about minus 150C ) the ice crystal will adopt the shape of a thin hexagonal plate, that grows larger and larger.
If we now consider a gradual and continued increase of humidity (while the temperature remains round about minus 150C ) to take place during the snow crystal's individual history, the crystal will grow faster and faster. But upon further increase of humidity, that is, upon further increase of the potential-energy difference, a critical point will finally be reached, at which the large energy difference cannot be handled anymore by the system : the 'channel' through which the discharge must take place is too narrow (precisely as we have it in heat transport, initially taking place by means of conduction, which (way of transporting heat) ultimately becomes, when the temperature difference is going to exceed some threshold value, an insufficient mode of heat transportation, and then turns into heat convection, as we see it in the Bénard Instability. We see it also in the case of the transition from laminar flow of water to turbulent flow when opening a tap, first a little bit, then more and more so). What then, upon this further increase of the energy difference, happens is that the stationary state (hexagonal ice plate) becomes unstable, and the system 'collapses' into a new dynamic regime, which here means that the crystal growth becomes such that the area of contact (between crystal and solution) increases rapidly, that is to say, the system-proper (the growing crystal) gets into a higher level of interaction with the environment (the solution) in order to realize a higher rate of energy discharge. This is accomplished by means of a dendritic way of growth of the crystal. Whereas a crystalline hexagonal plate can -- as hexagonal plate -- grow (in the sense of geometrically increasing its volume) in only one way (it just becomes larger, while its shape is preserved), a dendrite can grow, i.e. geometrically increase its volume, in many ways. It can form thin branches or thick branches, few side branches, many side branches, etc. And because -- as it has turned out -- under these conditions (round about minus 150C ambient temperature, and high levels of supersaturation) the resulting shape of the ice crystal is extremely sensitive to small variations in humidity, even already within this (just mentioned) narrow range, we can expect the many (different) geometric ways of forming dendritic crystals actually to be realized, expressed by the diversity of dendritic snow crystals. Indeed, no two morphologically identical dendritic snow crystals have ever been reported. In addition, we can expect it also within every single individual snow-crystal branch itself
: Such a branch (+ its side branches) (which is repeated six times in a single crystal) in fact documents the history of such an individual snow crystal : It sprouts from a smaller or larger initial hexagonal plate, then develops, say, into a long narrow branch with similar side branches, then, at a further stage in the crystal's growth history, the branch has developed sectored plates, grooves, ridges, etc. etc.
Where on the main branch, precisely the side branches and sectored plates will occur, depends on the accidental appearance of bumps, irregularities or other initial structures somewhere on the main branch (and the same holds for structures appearing on the side branches). The resulting structures are then repeated according to the point symmetry of the crystal.
All these substructures reflect the many fluctuations of the ambient condition of temperature and humidity as the crystal tumbles in the air on its way to the ground.
In all such cases of rapid crystal growth we must reckon with the fact that (crystallographic) imperfections will certainly occur within the resulting crystal.
In principle we could, by fine-tuning the mentioned conditions, create virtually all geometrically possible morphological shapes and structures. And it is because of this, that dendritic crystallization will do well in setting up an analogy between crystals and organisms.
Let us now compare dendritic crystallization with the Bénard Instability (which latter is a genuine thermodynamically far-from-equilibrium process, and was discussed toward the end of Sequel-30 of Part XXIX .
In the next document we will further discuss the development of dendritic ice crystals, especially their morphology.
In the document(s) after those concerned with the crystal analogy (coming up later) we leave the investigations into the latter, and, based on the results of these investigations, now accept this analogy as a general context for the previous and ensuing work. This ensuinig work will be a continuation of our investigation into the promorphs of two-dimensional crystals, but now explicitly involving their internal symmetry (plane group symmetry). In addition, the crystal analogy could point (if it allows to be so interpreted) to two different Layers of Being, that are either distinguished from each other by a (mere) jump in physical complexity (and nothing else), or by some really fundamental ontological NOVUM, resulting in the organisms to be elevated or over-formed (non-equilibrium) crystals.
e-mail : 
To continue click HERE for further study of the Theory of Layers, Part XXIX Sequel-32.