General Ontology XXIXm5e


(Takes a little while loading the images)

General Ontology Cosmos and Nomos

Theory of Ontological Layers and Complexity Layers

Part XXIX (Sequel-32)

Crystals and Organisms

e-mail :

Back to Homepage

This document (Part XXIX Sequel-32) further elaborates on, and prepares for, the analogy between crystals and organisms.

Morphological development of dendritic ice crystals.

In order to find the analogies that obtain between the Inorganic and the Organic (as such forming a generalized crystal analogy), it is necessary to analyse those general categories that will play a major role in the distinction between the Inorganic and the Organic : Process, Causality, Simultaneous Interdependency and the general natural Dynamical Law. This was done in earlier documents.
In previous documents we considered the important category of Dynamical System, discussed it also in terms of thermodynamics, and returned to an additional and continued analysis of the Category of Causality, which, in turn, led to an understanding of the direction of Time. In the previous document we continued this discussion of the Category of Dynamical System in terms of Thermodynamics, but then especially for the case of the generation of branched snow crystals (stellar snow crystals) and of windowpane frost (ice feathers, or ice flowers). We had determined their thermodynamic status by (1) investigating the origin and expenditure of the potential-energy stock upon crystallization, and (2) by comparing the features of f a s t growth of crystals with those of the Bénard instability. From all this we could then conclude that such crystals are -- as are the structures resulting from the Bénard instability -- genuine far-from-equilibrium thermodynamic systems, as are also all organisms. And having found this thermodynamic equivalence, branched crystals can indeed play a powerful role in the crystal analogy, as they already could do so because of their high morphological potential.

We will now extensively analyse the morphology of dendritic snow crystals, that is, the genesis of their shapes. The best way to do this would be to artificially make such crystals in the laboratory at controlled conditions of temperature and humidity (supersaturation of air with water vapor) and observe their development. Unfortunately I do not have the proper equipment to carry out such experiments. My situation is a bit like the early biologists who wanted to get insight into the morphogenetical development of organic forms, but having at their disposal only the organisms themselves, and not the equipment to follow their individual development leading to their shapes and structures. So what they did was to compare the observable morphologies of different species of available organisms as these morphologies presented themselves to the observer. From such comparisons conclusions were drawn as to their form generation. We will do the same with snow crystals as they are available to us in the form of photographs prepared and published by several authors.
The best way to investigate the morphology of dendritic snow crystals is to pay attention to the plate-like extensions that are seen in many dendritic crystals.
When conditions are such that fast growth, from some initially very small crystal seed (or from an initial hexagonal plate) will ensue, a branched crystal is the result. That is, we then have six main branches taking off from some small initial crystal seed, or from a larger or smaller initial hexagonal plate. These branches themselves will give off side branches, and they in turn will give a next order of side branches, etc. The direction of these branches always coincides with intrinsic directions of fast growth. This we have discussed in the previous document and also already in earlier documents. The resulting dendritic crystal is the product of fast growth enforced by high levels of humidity (and a temperature round about minus 15⁰C ). The branches are not faces, but directions of fast growth, where the faces, corresponding with these directions, have grown themselves out of existence.
This dendritic crystal can be interpreted as a crystal, that -- conceptually (only!) -- initially was a large fully grown hexagonal crystal, that is, a large perfectly hexagonal plate, but which later had been damaged : (conceptually) it had temporarily been taken out of its growing environment -- and thus halting further growth -- and then sectors of material were (conceptually) removed from the crystal, leaving only the dendritic star. And now we (still conceptually) put the damaged crystal back into its growing environment. However, this environment is now (prepared as) one that has a much lower humidity (but still one representing supersaturation), effecting the crystal growth to switch from branching to faceting, that is, instead of growing by developing branches, it now develops crystal faces. These crystal faces develop from the branches outwardly, that is, they come to be 'attached' to these branches. They look like fins, flippers or shovels, i.e. they are flat plate-like substructures of which their top and bottom surfaces are equivalent to the top and bottom faces of the regular hexagonal prism (which is the basic form of normally developed ice crystals), while their sides are equivalent to the prism sides of such a hexagonal prism. The sides of the 'fins' are thus (just as the top and bottom surfaces are) genuine crystal faces despite their small heights (this) as a result of the flat habit of dendritic (and many other snow crystals). What the crystal is doing is in fact the following : After the damaged crystal is put back to the growing environment which has been prepared to be such that the humidity is now moderate, the crystal is 'healing' itself out, by filling up the spaces between the branches, in order to make a fine hexagonal crystal (hexagonal tablet) again, or, in other words, to restore the disturbed equilibrium between the inwardly directed surface-tension pressure and the outwardly directed intrinsic anisotropic growth forces.
Diffusion rate (of water molecules to the crystal surface) only plays a significant role in fast-growing (diffusion-limited growth), that is in the branching mode of growth. Its role is not significant in slow growth, that is in the faceting mode of growth.
Not a single individual dendritic snow crystal can represent all forms of such crystals. What is missing in one, is present in some other, and vice versa. Nevertheless photographed individuals are very instructive to begin with. See next Figure.

Figure above : A dendritic snow crystal (seen in the direction of the main axis) with subsequent development of faces.
These facial structures here present themselves as distorted regular hexagons, that is regular hexagons, of which the sides have become unequal in length, but in which the angles of 120⁰ are preserved. Also the intrinsic orientation of the sides of these distorted hexagons are preserved, that is they represent the intrinsic directions of the six prism faces, indicating that they all stand in crystallographic continuity with each other and with the dendrite (i.e. the six arms).
See also a blow-up of a part of this crystal HERE (click on image to see it in full size [The very fine 'texture' which might be visible in this blow-up, has nothing to do with the crystal or crystallite. It is the print 'raster' of the photo-reproduction.] ).
(After LIBBRECHT, K., The Snowflake, 2003 [Photo by Patricia Rasmussen])

The next Figure indicates the branches of this crystal insofar as they are visible from the photograph. You can see it (Figure + subscript) HERE .

As has been said, the growth, going into faceting mode, results -- in the present case -- in the development of flat structures, that are (as seen from above) distorted regular hexagons, that is, regular hexagons of which the sides have become unequal, but whose angles (120⁰) are preserved. All such structures, that is, substructures of a crystal, which are crystallographically continuous with each other and with the crystal-as-a-whole, we will call crystallites. The next Figure isolates one such crystallite.

Figure above : An isolated faceting structure (distorted hexagon, crystallite) from the crystal of the previous two Figures. The hexagon is attached to one of the crystal's main branches. Four of the six corners are developed, and five of the six sides. These sides correspond to vertical prism faces (prism faces parallel to the c-axis), that is they are crystallographically equivalent to the vertical prism faces of the crystal (which would have been developed in normal crystallization). Because there are also other types of plate-like substructures in dendritic snow crystals (namely so-called sectored plates), we will give the ones here discussed a special name : shovels.

The crystal depicted in the above Figures, when looked down to it along its c-axis ( = main axis), has at least two sets of growth directions perpendicular to the main axis, each set containing three pairs of directions, each pair consisting of two opposite directions. One of these two sets will eventually deliver six permanent crystal faces (which, naturally, stand perpendicular to their corresponding growth directions, and are vertical prism faces, that is, faces parallel to the crystal's main axis), while the other set corresponds to six fast-growing faces (growing faster than those corresponding to the first set), which will, hoewever, eventually grow themselves out of existence. The six permanent vertical crystal faces ( The top and bottom faces of the hexagonal prism are also permanent crystal faces, but are horizontal ) are indicated, as to their directions, in the next Figure, and are seen there as lines (black), because we look in a direction parallel to the crystal's main axis.
Recall that in crystals only directions matter : The six faces, indicated by black lines in the Figure, just represent the directions (perpendicular to which are the corresponding growth directions) of the permanent vertical prism faces, when these faces would have been developed. And although the crystal of the above Figures did not develop into a regular hexagonal (flat) prism, but in a dendritic crystal, these six permanent vertical crystal faces (and also the two faces capping the prim, that is, the faces that are perpendicular to the main axis) are nevertheless explicitly represented (as to their directions) throughout the crystal. We see them in every distorted hexagon ('shovel') as the latter are present everywhere in the crystal. Although the sides of these hexagons are not equal in length anymore, their orientations have not changed, neither have their angles. The next Figure depicts the directions of the six permanent prism faces (indicated by black lines, drawn somewhere [i.e. arbitrarily] in the crystal). You can see it (Figure + subscript) HERE .

The six permanent vertical prism faces are crystallographically equivalent, which means that their atomic aspects, as they present themselves to the nutrient environment, are identical, and also that their geometric relationship to the crystallographic point lattice (See Figure from previous document , there shown for a rectangular point lattice) is identical. This implies that when these faces meet an identical environment, that is, if this environment is chemically and physically uniform (same conditions of diffusion, same chemical composition, same temperature, same humidity and same pressure, for all six growth directions), these faces will grow with the same rate.
For non-equivalent crystal faces this is not so : They have different atomic aspects and their geometric relationship to the system of lattice points is different. In our case a horizontal prism face (that is a face perpendicular to the crystal's main axis) is not equivalent to a vertical prism face, and a slow-growing vertical prism face is not equivalent to a fast-growing vertical prism face.
All this means that in a uniform growing environment a not too fast growing ice crystal is expected to show a definite habit, that is, fast-growing faces grow themselves out of existence when bounded by tapering slow-growing faces, and the ratio between the height of the crystal (measured along its crystallographic main axis) and the width of the crystal (measured along a horizontal crystallographic axis) is expected to be constant. See next Figure.

Figure above : The regular hexagonal prism as the basic form of ice crystals. The prism consists of two basal faces perpendicular to the c-axis, and six vertical prism faces parallel to the c-axis. All ice crystals are internally based on a hexagonal point lattice.

However, in the case of ice crystals (but not peculiar to them), when the temperature is not very low, that is not below, say, minus 20⁰C, there exist temperature-dependent surface structures such as the so-called quasi liquid layer (QLL), on the surface of the growing ice crystal (surface melting transition, occurring on the crystal surface) (See HERE ) (surface structures discussed by FURUKAWA, Y., on this website ). And such surface structures are different on crystallographically non-equivalent faces, and their presence and thickness are dependent on the temperature. All this causes a temperature-dependent h a b i t of the ice crystal. This habit can change from plate-like ice crystals to columnar ice crystals, as we know it already from the Nakaya Morphology Diagram . But be that as it may, crystallographically equivalent crystal faces will always behave in exactly the same way under the same conditions.
Well, our distorted hexagons, as they occur in the snow crystal depicted above, have six equivalent faces (seen as the six sides of the hexagon), and they have evidently behaved differently with respect to each other. To explain this we must first resort to a consideration of the growth environments of these faces, that is, investigate whether the differences in their growth rates are caused by differences in the micro-environment (local conditions of diffusion, local degree of supersaturation, local temperature, local pressure [with respect to the latter we can safely assume that the pressure is the same everywhere in the crystal, so we can ignore pressure] ).
As to the crystal depicted above, we must assume that the overall conditions initially were such that a star-shaped dendrite evolved, having main and side branches (all corresponding to fast-growth directions). After that, the conditions became such that the crystal grew at a lower rate, and thus was allowed to 'heal' itself by the faceting mode of growth : On the branches and side branches distorted hexagons developed, filling up the crystal. We can see, that during this second growth phase local diffusion differences could not have played a significant role, because we see that the distorted hexagons ('shovels') have grown everywhere between the arms, that is, also where the available space was narrow and more or less secluded from the rest of the growing environment. Further, around any single hexagon we cannot expect local temperature differences to exist with respect to one side of a hexagon to another of that same hexagon -- temperature differences, that could cause differences in growth rate of these sides (that is, vertical prism faces) of a same hexagon. The only condition that can, in the present case, distort the hexagons is their eventual crowding. When two of them grow more closely together, the space between them gets narrower, resulting in a poorer supply of nutrient material (water molecules of the water vapor in the air), or, equivalently, in a poorer discharge of energy. The growth of both of them will finally halt.

But there are cases in which we also see distorted hexagons, but where crowding (and also diffusion problems) have not occurred, such as in the snow crystals (especially the left one) of the next Figure.

Figure above : Snow crystals carrying distorted hexagons ('shovels'). This is a case where neither diffusion differences, nor crowding could have caused the distortion (that is, a difference in growth rate of crystallographically equivalent crystal faces).
(After LIBBRECHT, K., The Snowflake, 2003 [Photo by Patricia Rasmussen])

The next five Figures also depict snow crystals with 'shovels'. And also in these cases neither crowding, nor diffusion problems could have caused the distortion.

Figure above : Snow crystals carrying distorted hexagons.
(After BENTLEY, W., Snowflakes in Photographs, 1931.)

Figure above : Snow crystal carrying distorted hexagons.
(After LIBBRECHT, K., The Snowflake, 2003 [Photo by Patricia Rasmussen])

Figure above : A snow crystal carrying distorted hexagons.
(After BENTLEY, W., & HUMPHREYS, W., Snow Crystals, 1931, 1962.)

The next Figure beautifully shows the overall shape of the shovels. Clearly they are distorted hexagons. And here the cause of their distorted growth could be their crowding.

Figure above : Snow crystal carrying distorted hexagons.
(After LIBBRECHT, K., The Little Book of Snowflakes, 2004.)

In addition to the first snow-crystal Figure of the present document, the next six Figures show that when faceting growth has set in, diffusion of material into more or less narrow regions between already formed crystal structures, does not seem to be a problem anymore (as it is in fast-growing), which means that it cannot -- in these cases -- be a cause of distortion (of hexagons).

Figure above : Snow crystal showing easy growth of substructures in more or less narrow spaces between earlier structures of the crystal.
(After LIBBRECHT, K., The Snowflake, 2003 [Photo by Patricia Rasmussen])

Figure above : Snow crystal showing easy growth of substructures in more or less narrow spaces between earlier structures of the crystal.
(After BENTLEY, W., Snowflakes in Photographs, 1931.)

Figure above : A dendritic snow crystal. From the initial set of slender branches, faces begin to develop.
This stellar dendrite is about as large as you're likely to find falling from the sky. It measures 7.2 mm (0.28 inches) from tip to tip.
(After LIBBRECHT, K., The Snowflake, 2003 [Photo by Patricia Rasmussen])

In all the above photographs, but especially in our first one , fifth one and eighth one (the latter two counted from below), and also in the last one, we see another peculiar feature : While all main and side-branches of a snow crystal represent directions of fast growth, the side-branches of any main branch always point (albeit obliquely) to the tip of the latter (and this also with respect to side-branches and their side-branches), despite the fact that it is in principle possible to be otherwise, while still representing directions of fast growth. See next Figure.

Figure above : The direction of branches and side branches in snow crystals.
Two dendrites (branch + side branches) shown as to their crystallographically possible directions. The left dendrite represents the configuration we always see in snow crystals. The right dendrite is an alternative configuration, in principle possible, but never encountered in natural snow crystals.
The branches always (also in the alternative configuration) are along the directions of fast growth perpendicular to the c-axis (which itself is perpendicular to the plane of the drawing). These directions are indicated in the top-left image.

The next Figure shows examples of these two configurations of branches and side branches in laboratory-grown ice dendrites.

Figure above : Two laboratory-grown ice dendrites, of which the left one shows the odd configuration discussed in the previous Figure.
The one the right was grown at minus 15⁰C (5⁰F), while the one on the left was grown at minus 5⁰C (23⁰F). They were grown at high humidity, which resulted in extensive sidebranching. Each is just over 0.1 mm (0.04 inches) long.
(After LIBBRECHT, K., The Snowflake, 2003)

In the next Figure we have a natural snow crystal in which the alternative configuration described above seems be be present with respect to one side-structure only. However, the configuration is perfectly normal, because the side-structure in question does not shoot off from the main branch (in which case it would indeed be oddly oriented), but from some other side-structure which itself shoots off from the main branch.

Figure above : The orientation of one of the side-structures (a 'shovel', see arrow) seems to be at odds with the general plan in the snow crystal (and in snow crystals in general), but it isn't : It is not attached to the main branch (if it were, it would be at odds), but to a -- short -- side-structure (itself also being a shovel). The rounding-off of shovel contours is caused by partial evaporation of the crystal.
Although the shovel indicated by the arrow complies with the rule that every side-structure is (obliquely) directed toward the tip of the structure onto which it is (directly) attached, it does not comply with the tendency of snow crystals to preserve the 6mm symmetry of their two-dimensional aspect. We clearly see that the branch + appendages, of which our shovel is a part, is not symmetric anymore (one of the two types of mirror lines eliminated). And this branch is also not symmetric anymore with the next branch (destroying at least one of the other type of mirror line), as can be seen HERE .
(After LIBBRECHT, K., The Snowflake, 2003. Adapted part from a photograph taken by Patricia Rasmussen and displayed on the cover of the book.)

We will now construct several substructures and their configurations actually encountered in snow crystals, and, in addition to that, several configurations of (possible, and actually encountered) substructures that are not encountered in snow crystals, but which (configurations) are nevertheless crystallographically possible. But before doing so we first discuss some general features of ice crystals as they relate to the ice lattice, seen from above, that is, looked down along the c-axis.
Ice crystals are built up by the periodic stacking of three-dimensional rhombic building blocks, that can be seen as parts of regular hexagonal prisms :

Figure above : The ice structure consists in the periodic stacking of three-dimensional rhombic building blocks. One such block is shown (blue). Every rhombic building block is a part of a regular hexagonal prism.

The top surface of such a stacking thus consists of rhombs. In the next Figure we show this surface. For construction purposes each rhomb is divided into two equilateral triangles.

Figure above : Top surface of the ice lattice (where the c-axis is perpendicular to the plane of the drawing). It is built up by equally oriented rhombs, but it can also be seen as built up by hexagons.
Below in the Figure : three individual layers of three-dimensional rhombic building blocks, of which only their top faces (rhombs) are visible, as it is in the rest of the Figure.

Figure above : Again, top surface of the ice lattice (where the c-axis is perpendicular to the plane of the drawing). It is built up by equally oriented rhombs.
A few ways to indicate crystal faces (dark blue lines), parallel to the c-axis, are shown.

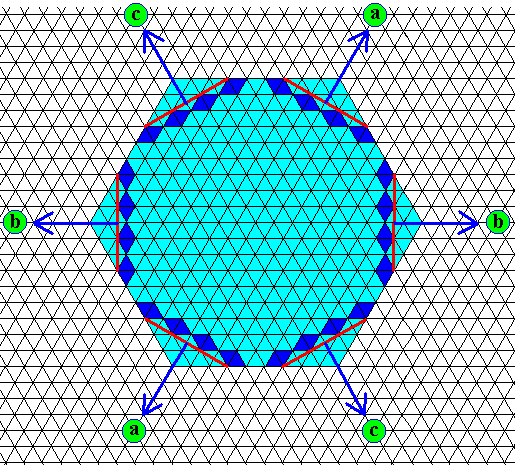
Figure above : Regular hexagon (light blue). Basic form of ice crystal as seen down along the c-axis. The directions of fast growth (perpendicular to the c-axis) are indicated (three pairs, a, b and c). The possible faces corresponding with these directions of fast growth are indicated. They eventually will grow themselves out of existence. The faces of the regular hexagon are the slow-growing faces. Their corresponding growth directions are perpendicular to them.

A regular ice hexagon can be imagined to have grown from a small hexagon-shaped seed by the apposition of whole building blocks (rhombic shape) and half building blocks (triangular shape). The intrinsic growth rate of the six (slow-growing) equivalent faces (seen as sides of the hexagon) is equal for all six of them. If the actual growth rate of these faces is equal too (for example when the crystal slowly grows in a uniform undisturbed growing environment), then a (large) regular hexagon will result. See next Figure.

Figure above : A regular ice hexagon is the result of the six equivalent slow-growing faces having actually grown with the same rate, starting from a hexagon-shaped (free) crystal seed (yellow). Such an ice hexagon (a snow crystal) is to be expected in a uniform medium with low humidity.

The next Figure shows what happens when two (opposite) faces (out of the set of six equivalent faces) come to grow twice as slow as the remaining four (equivalent) faces.

Figure above : Growth of an ice hexagon from a hexagon-shaped (free) seed (yellow) when two (opposite faces) of its (six) equivalent intrinsically slow-growing faces grow twice as slow as the remaining four (equivalent) faces. This is supposed to mean for example that, although the faces a and b are equivalent, meaning that their intrinsic growth rates are equal, face a has (by some external cause) come to grow slower than the standard growth rate of equivalent face b at the conditions prevailing at b. The result is a distorted regular hexagon (i.e. it is distorted when compared with a regular hexagon). While all angles of the crystal remain unchanged, and are the same as in the undistorted hexagon (previous Figure), the lengths of the sides are not equal anymore.

Figure above : Truncated (regular) ice hexagon. The intrinsically fast-growing faces d, c and their equivalents, are about to disappear upon further growth. The intrinsically slow-growing faces a, b and their equivalents, are well developed and will not disappear upon further growth.
The growth direction of some of the faces is indicated by arrows, while the relative growth rate of these faces is indicated by the length of these arrows. Indeed, the faces, while still chopping off the corners of the regular hexagon, that is, the faces d, c and their equivalents, have longer arrows than the faces a, b and their equivalents. As long as faces are still developed, their relative growth rate can be measured by the length of the line starting out from the growth center (that is -- in fact -- from the periphery of the seed) and landing perpendicular to the face. When the hexagon grows further the intrinsically fast-growing faces will disappear, resulting in a genuine regular hexagon. The growth rate of the intrinsically slow-growing (prism) faces is here set at three layers in some unit of time.

The next Figure illustrates (yet another example of) the development of a distorted hexagon : One intrinsically slow-growing face and its opposite face come to have a growth rate that is (now) only one third of the standard growth rate of the other four (intrinsically slow-growing) faces (at their prevailing conditions of temperature and humidity) crystallographically equivalent with them.
The Figure compares it with the non-distorted hexagon.

Figure above : Development of a distorted hexagon in virtue of two opposite intrinsically slow-growing faces coming to have a growth rate three times less than that of their equivalents. The distorted hexagon is compared with the undistorted regular hexagon.
a and b refer to the directions (face directions, growth directions) and actual relative growth rate of two developed intrinsically slow-growing faces of the regular as well as of the distorted hexagon.
g and d refer to the directions (face directions, growth directions) and actual relative growth rate of two developed intrinsically fast-growing faces of the regular hexagon.
d is common to the regular and the distorted hexagon.
h refers to the direction (face direction, growth direction) and actual relative growth rate of one slow-growing face of the distorted hexagon. It has the same direction as the intrinsically slow-growing face i of the regular hexagon, but grows three times slower than the latter (Count the triangles, starting from the periphery of the seed [yellow] ).
Also for the distorted hexagon the intrinsically fast-growing faces g, d and equivalents will eventually vanish upon further growth (for example, g is flanked by two tapering and slower-growing faces h and a, and will thus eventually disappear upon further growth of the crystal.

The next Figure indicates the effective growth rates, and their directions, of two actually developed faces of the distorted hexagon of the last but two Figure. The direction of a possible fast-growing, but not developed face is indicated.

Figure above : The distorted hexagon of the last but two Figure. The present Figure is about intrinsically slow-growing and fast-growing vertical prism faces, that is, possible crystal faces, parallel to the c-axis, and thus perpendicular to the plane of the drawing. Only the intrinsically slow-growing faces are actually developed (they differ in their actual (extrinsic) growth rate and are visible as lines). These growth rates, and their directions are indicated by arrows and their relative lengths. The growth direction of a crystal face is always perpendicular to the direction of that face.
The growth direction of an intrinsically fast-growing face (c) is indicated by an arrow. The length of this arrow does, however, not indicate the relative growth rate of this possible crystal face because the latter is not actually developed.
The arrows indicate how far the several actually developed faces have made it from the center of the crystal where growth began.
The faces a and b are crystallographically equivalent. They are not equivalent to (possible) face direction c.

While in the above Figure one fast-growing possible face (c) and its growth direction was indicated, in the next Figure yet another, but equivalent, fast-growing possible face (d) and its growth direction is indicated.

Figure above : The distorted hexagon of the previous Figure. The present Figure is again about intrinsically slow-growing and fast-growing possible vertical prism faces.
The growth direction (arrow) of yet another, but equivalent fast-growing possible crystal face (d) is added. The fast-growing face directions c and d are equivalent. Their intrinsic relative growth rates are equal. Also these fast-growing faces are possible vertical prism faces (parallel to the c-axis). Because they grow faster than the (tapering) adjacent (vertical) prism faces (such as a and b ), they have vanished.

Figure above : Same as previous diagram, but here the line e-f is added. It also indicates the growth direction of the possible (fast-growing) face d (that is, the face in the direction of d ). In shovels (distorted hexagons) we very often (if not, always) see, in addition to its longitudinal ridge and some other ridges, a prominent ridge running along this line (and also along its symmetrical counterpart). Such a side-ridge (branching thus from the longer axis of the distorted hexagon) is fundamentally different from the side-ridges we see in sectored plates. The latter are also plate-like extensions of arms in branched snow crystals, and will be discussed in the next document.

The next Figure also gives a distorted hexagon, but now with a slightly different growth-rate ratio, and again indicates some directions which can be discerned in it.

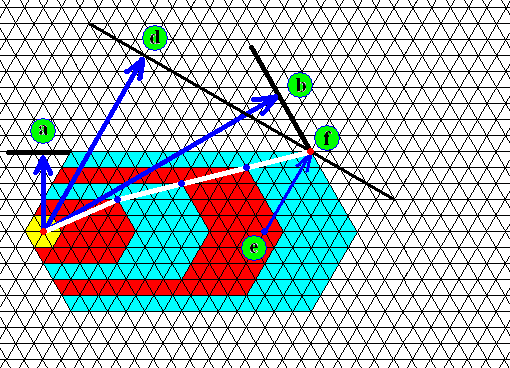
Figure above : Distorted hexagon as part of a snow crystal. From the growth center (yellow) of the hexagon towards the latter's periphery we can, as we did already above, distinguish several directions.
First of all we have the directions of the several possible crystal faces (vertical prism faces) and their corresponding growth directions perpendicular to them : a indicates the face direction and growth direction of an actually developed and intrinsically slow-growing face. And b indicates the face direction and growth direction of another actually developed and intrinsically slow-growing face. The length ratio of the arrows representing these two growth directions at the same time indicates the non-intrinsic growth-rate ratio of the two corresponding faces (their intrinsic growth rates are identical, because they are crystallographically equivalent crystal faces).
The arrow, going from the growth center (yellow) and landing perpendicular onto the face direction d -- representing the direction of an intrinsically fast-growing crystal face -- indicates the growth direction, but not the relative growth rate, of such a possible face because that face is not actually developed. Further, it is not equivalent to the faces a and b.
The line e-f also indicates the growth direction of that possible (intrinsically fast-growing) face with direction d, and for the same reason does not indicate (by its length, say) the relative growth rate. In all this, when we want to compute and to compare growth rates of developed faces, we must start counting (triangles) from the periphery of the hexagonal crystal seed (yellow) to the face along the growth direction.
Now in the present Figure one other more or less linear feature is indicated (white). This linear feature is some sort of microscopic distortion lying between two adjacent faces, and grown outwards together with these faces (or, perhaps causing a difference in the growth ratio between these two faces). It makes odd angles (that is, angles not compatible with the crystallography of ice) with the shovel's longitudinal axis (itself representing a direction of intrinsic fast growth), so this linear structure is not an intrinsic feature of ice crystals. It is effected by, and records, the individual history of that part of the given individual ice crystal, and thus it is not equivalent to the branches of a stellar crystal, because these branches represent intrinsic directions of intrinsically fast-growing prism faces. We will actually encounter such historical linear features in so-called sectored plates, which will, as has been said, be discussed in the next document.

The next Figure shows the growth of such a distorted hexagon from a bump on a pre-existing branch.

Figure above : The distorted hexagon (as depicted in the previous two Figures) has grown from a (random) bump that happened to be present on a pre-existing branch of a snow crystal. If we, in the present Figure, consider the branch growing in the SE (southeast) direction, then the orientation of the shovel, as depicted in the Figure, is what we indeed see in all snow crystals. The next Figure shows an alternative orientation, which is crystallographically equally possible, but which is not encountered in natural snow crystals.

Figure above : The shovel of the previous Figure. Alternative orientation with respect to the branch to which it is attached. This branch is, as in the previous Figure, supposed to grow in the SE direction.

When, at a certain location on the branch, there is a shovel at either side (or a sidebranch for that matter), it is always in this way :

Figure above : Two shovels on either side of the branch (they need not to be exactly identical with respect to each other). In this way -- that is, this orientation with respect to the branch, which latter is supposed to grow in the SE direction -- we see it in snow crystals, and never in the following way (next Figure), despite the fact that it is crystallographically possible :

Figure above : Two shovels on either side of the branch (they need not to be exactly identical with respect to each other). This configuration, although crystallographically possible, is not seen in natural snow crystals.

In the next Figure these orientations are again depicted, but now seen in the context of the whole crystal.

Figure above : For sidebranches or shovels both a and b are crystallographically possible orientations, because both represent the directions of fast growth. However, we could surmise that the orientation as indicated by a will not be realized in real snow crystals because such growth in the space between two (main) branches will be excluded because of diffusion problems. The crystal would prefer the orientation b because that is a growth in an outward direction with respect to the crystal, where thus the growing structure can more easily be supplied with material, that is, water molecules. However, growth between two (main) branches, such that it is not outwardly directed, as in the case of a, is possible, as can be seen in a snow crystal depicted earlier, click HERE (click on image to enlarge it a little bit). It is also present in another snow crystal, also depicted earlier . Finally we can see it in the next Figure :

Figure above : Dendritic snow crystal (with mixture of branching and faceting). Here we clearly see that growth, not outwardly directed, but neutrally directed, and (taking place) between two main branches, is possible. For where to find it in this crystal, click HERE . The outgrowth, having grown in this direction, did not sprout from the main branch but from the base of a secondary branch. There are twelve of them.
(After LIBBRECHT, K., The Little Book of Snowflakes, 2004.)

The next two Figures (under two buttons) show that a configuration like that of a in the above diagram , that is, a substructure that is not (obliquely) directed towards the tip of the structure from which it sprouts (whereas b does so sprout), does actually occur (albeit extremely rarely). In the photograph depicted by both these Figures we indeed see a structure like we had drawn earlier . However, the possibility is not excluded that the (aberrant) (sub)stucture we see in the photograph (in the upper arm of the crystal) is just a small fragment coming from some other crystal, a fragment that is being frozen onto our crystal. Click HERE to see this crystal, and HERE to see where in the crystal the alleged aberrant substructure is.

In the next Figure we again have our distorted hexagon of earlier Figures. But now the upper left face has come to lag behind, because of unfavorable diffusion conditions. It is, however, to be expected that under such a condition no crystal facet will develop, but just an irregular boundary.

Figure above : The distorted hexagon (as depicted in earlier Figures) has grown from a (random) bump that was present on a pre-existing branch of a snow crystal. The growth of the upper left face is slowed down as it approaches the branch, because this approaching creates unfavorable diffusion conditions. However, we could expect that there where diffusion conditions are unfavorable no smooth crystal facet will develop, but just an irregular boundary.
The growth direction of the branch is supposed to be SE.

The next Figure lets a distorted hexagon grow from the tip of a pre-existing branch.

Figure above : A distorted hexagon grows from the tip (yellow) of a pre-existing branch of a snow crystal. At the same time as the hexagon grows, the supporting branch grows with it, resulting in an extension of it. However, I am not entirely certain whether the terminal shovels, as we see them in so many snow crystals, do actually develop in this way.

The next photograph shows a terminal shovel in some more detail.

Figure above : A terminal shovel of a snow crystal ( To see the complete crystal click HERE ).
This particular shovel shows a second growth phase.
(After LIBBRECHT, K., The Little Book of Snowflakes, 2004.)

The next Figure displays a growth sequence of a branched ice crystal. It is a series of photographs showing a growing snow star (grown in the laboratory) over a period of about fifteen minutes (After LIBBRECHT, K., The Snowflake, 2003.). To see it click HERE (If necessary, click on the image to see it in its full size).

Innate symmetry strive in snow crystals.

Ice crystals consist of water molecules that are arranged according to a hexagonal point lattice, that is a three-dimensional space lattice consisting of points (and in which's drawings -- for clarity -- these points are connected by lines, see Part XXIX Sequel-7 ). In order to discuss the symmetry of ice we first must consider the empty (three-dimensional) hexagonal point lattice, that is, just the stacking of empty building blocks, of which the smallest possible is the rhombic prism. The symmetry of this empty hexagonal point lattice is according to the space group P6/m2/m2/m. Then we must insert motifs in it according to how ice is built, to represent the total symmetry of ice, that is, the space-group symmetry P 6₃/m 2/m 2/c (where c is a glide plane instead of a mirror plane(m)), which indicates the symmetry including all translational symmetries, like screw axes, etc. While doing so, we must imagine the lattice with its inserted motifs to extend indefinitely in three-dimensional space. In such an indefinitely extended ice lattice we see an infinite number of 6₃ screw axes (parallel to the c-axis), an infinite number of mirror planes perpendicular to these screw axes, an infinite number of vertical mirror planes (parallel to these axes), also 2-fold rotation axes, and glide planes.
If we now consider only the two-dimensional extension of this space lattice (because we concentrate only on the two-dimensional extension of snow crystals [perpendicular to the c-axis] ), we obtain a plane lattice, namely the hexagonal net. If, further, we provide this net with two-dimensional motifs we get a plane group (an empty [hexagonal] net also has plane group symmetry, but by providing it with motifs we can either preserve this symmetry or lower it, depending on the symmetry of these motifs). And when these motifs have -- as in two-dimensional ice -- 6mm symmetry, that is the symmetry of a regular hexagon, then the resulting symmetry of the filled-in net is the same as that of the empty net, that is, such motifs do not lower the symmetry of the net. As such, we then have to do with the plane group P6mm . This plane group was discussed in First Part of Website : Last Series of Documents : Internal Structure of Crystals Part XX, and also in Second Part of Website : (Prelude to) the Total Symmetry of 3-D Crystals, Part XXIII, Group Theory (P6mm).
This P6mm plane group structure is depicted in the next diagram :

Figure above : Pattern according to the plane group P6mm. A hexagonal net is provided with motifs having 6mm symmetry (that is, the symmetry of a regular hexagon). The lattice and its (inserted) motifs, as it is drawn here, must be imagined to extend indefinitely in three-dimensional space.

The inherent symmetries of this plane group are given in the next Figure.

Figure above : The symmetries of the plane group P6mm (the rotation axes are perpendicular to the plane of the drawing).
Here we see 6-fold rotation axes (at the corners of the rhombs), two types of mirror lines (red and black solid lines), glide lines (dashed lines), 2-fold rotation axes (at the center of each rhomb, and at the center of each side of the latter), and 3-fold rotation axes (two in each rhomb). The lattice must be imagined to extend indefinitely.

So a two-dimensional ice lattice (obtained by eliminating all vertical (i.e. parallel to the c-axis) translations) shows exactly these symmetries (and if we also would eliminate all horizontal translations, we would get the point symmetry of two-dimensional ice, 6mm, that is : one 6-fold rotation axis, three mirror lines of one type, and three of the other type.). The two-dimensional ice lattice shows us possible crystal faces (representing the vertical prism faces of three-dimensional ice, and visible in the two-dimensional image as lines), while the geometry of this lattice and the nature of the chemical motifs (placed into this lattice) determine the relative growth rates of these possible crystal faces.
From all this it is clear that when considering only the two-dimensional extension of an ice crystal perpendicular to the c-axis (in fact [considering only] the projection of the three-dimensional ice lattice onto a plane perpendicular to the c-axis), we can expect a regular hexagon to develop when such a crystal is growing in a perfectly uniform environment with low humidity (relatively slow growth). And this hexagon has indeed 6mm symmetry.
But we now know that this symmetry of the ice crystal as it reflects itself completely in the external shape of the crystal (possible because water crystallizes in the most symmetric Class (that is, holohedric Class) of the Hexagonal Crystal System), is dependent on the conditions that happen to prevail during growth (temperature, humidity). If these conditions, at one and the same moment in time, differ as we go from one region of the crystal to another of that same crystal, then we can expect some symmetry to get lost (while nothing whatsoever happens with the ice lattice itself), resulting in an ice crystal that looks externally asymmetric. That's why substructures like the one depicted above can in principle occur in an ice crystal, breaking the 6mm symmetry of its two-dimensional aspect ( The mirror line going through the branch is eliminated).
The fact, however, that this does not (or very rarely) occur in at least natural snow crystals is thus significant.
And, what is also significant is another fact (already discussed earlier on this website ( Part XXIX Sequel-6 ) : Side-branches and other side-structures are supposed to be developing from randomly occurring ice bumps on the main branches of a stellar dendritic snow crystal. But because such bumps are random (in time and in space), their distribution on the six arms is expected to be different. Indeed this is the case, but only to a very low extent. Also on secondary and higher-order branches the bumps are expected to have a different distribution pattern if we go from one such branch to another (on the same crystal individual). But also here this difference turns out to be in fact remarkably small. All this results in the fact that the six arms (branch + appendages) of any given individual snow crystal look remarkably similar (even when sometimes one arm is significantly longer or shorter than the other five), that is to say, the morphological type of branch structure (branch + appendages) is the same for all six branches of a given snow crystal (but differs strongly from crystal to crystal).
So just like the refusal by the growing snow crystal to generate substructures like the one depicted above , destroying at least a mirror line, the strong similarity, up to almost identity, of the six arms (branches and their appendages) of a single snow crystal seems to demonstrate that the crystal is actively striving towards the preservation of its two-dimensional 6mm symmetry, and in addition to it, strives to develop according to a particular growing sequence : A side-branch or side-shovel (or any other side-structure) directed parallel to a possible permanent (vertical) prism face (See Figure displayed earlier ) does not develop directly from a main branch but only from a secondary branch (and in this, a certain degree of assymetry can still be possible, as it turns out, meaning that this strict growth sequence does not necessarily result from the demand to preserve symmetry). It is as if the growing crystal possesses a 'pre-existing plan' according to which it builds itself up. It has, so to say the power to generate and maintain a certain definite morphological lay-out, also when the conditions are more or less adverse. But of course this power has its limits, resulting in the occurrence of many mis-shaped snow crystals.
Apart from this holistic aspect of a growing snow crystal, the preservation of 6mm symmetry is aided by the (non-holistic) fact that the developing snow crystal is tumbling and rotating (while it is driven by wind and gravity) during its descent to the ground, resulting in the fact that at every single moment all parts of it (lying on a circle that has its midpoint in the crystal center) will have experienced the same temperature/humidity conditions, which means that everywhere around the crystal there is the same balance between faceting and branching. So when terminal ice plates (representing a faceting phase) develop, then each of the six main branches obtains such a plate. But the fact that the details of such plates are so similar among each other (similar as to one plate compared with another in the same crystal) cannot be explained in this way, because these details have supposingly a random origin.
So our result is that there is, to begin with, an external tendency to preserve 6mm symmetry (of the two-dimensional aspect) because the crystal tumbles and rotates in its growing environment and so having all its parts experiencing exactly the same conditions at any one moment in time. But in addition to this, there is an intrinsic strife of the crystal to assume and maintain 6mm symmetry, and to stick to a definite growing sequence. This intrinsic strife is surely remarkable, because such a feature is only known for the case of organisms, namely their intrinsic strife to take on and maintain their specific shape, symmetry and structure. In the next document we will return to this interesting phenomenon, and will try to explain it along metaphysical lines.

Continuation of the morphology of dendritic snow crystals.

Next we see a peculiar snow crystal. It apparently began with a dendrite consisting of six arms, each provided with a terminal shovel (in fact there are only five such shovels, and one sectored plate). After this, the growing conditions apparently changed such that, apart from some additional narrow spaces being left over, the crystal almost entirely 'restored' itself, resulting in a hexagonal plate.

Figure above : A snow crystal having restored itself, resulting in a more or less complete hexagonal plate.
(After LIBBRECHT, K., The Little Book of Snowflakes, 2004.)

In the next document we will continue our morphological analysis of branched snow crystals. We will discuss the genesis and morphology of sectored plates.

To continue click HERE for further study of the Theory of Layers, Part XXIX Sequel-33.

e-mail :