back to homepage

Introduction

What do we need to know in order to be able to correctly interpret Crystals as Substances?

A CRYSTAL displays individuality, it encounters us as an individual being, and is as such a good example of an inorganic First Substance .
Of course it is possible to interpret crystals only as being modifications of substances (as is done in Chemistry) and thus not as being Substances. In this interpretation the substance is the chemical compound (or chemical element). Accordingly we could, for example, say that Calcium Carbonate at normal temperatures finds itself in the solid state, and in this state it can occur in two (sub)states, namely either as Aragonite or as Calcite (It can even be in a non-crystalline state).
Aragonite is Calcium Carbonate crystallized in the Rhombic-dipyramidal Crystal Class of the Orthorhombic Crystal System, while Calcite is Calcium Carbonate crystallized in the Hexagonal-scalenohedral Crystal Class of the Hexagonal Crystal System (Rhombohedral Division). Aragonite and Calcite would then be states (modifications) in which Calcium Carbonate (CaCO₃) can be in, i.e. Calcium Carbonate can exist in two ways.

But because Aragonite and Calcite differ strongly in their internal structure, which already showed up in their belonging to two different Crystal Classes and even to different Crystal Systems, it seems to me obvious that they are metaphysically different Substances (of course with a common element, namely their chemical composition). They themselves can (also) occur in different modifications, which are however accidental (= per accidens ) with respect to the internal structure : Those modified forms still possess the same internal structure, the (total) symmetry of which is described by the so-called Space Group (explained later on).

Along these lines of reasoning we arrive at a new (but according to me, correct) concept of Substance with respect to chemical crystalline matter.
Suppose we have (before us) a certain (individual) crystal, and suppose we ask what this crystal is (in the sense of Aristotle's what-is-it question), then we should be satisfied (for the time being) when we know the nature of its constituents, i.e. when we know which atomic species participate in the constitution of the crystal, and in what proportion, in short, the crystal's chemical composition.

Remark :   Later in this Essay we will answer the what-is-it question along the lines of dynamical systems theory. However, the Chemical Composition + Space Group, to be considered below (as the answer to the what-is-it question) remains the visible manifestation of the crystal's Essence.

Further we should know how precisely the individual atoms (and / or ions [ Ions are electrically charged atoms or groups of atoms.]) are arranged in the crystal, i.e. we should know according to what kind of geometrical pattern the atomic constituents are ordered while building up that crystal.
Knowing this complete (internal) structure is equivalent to knowing what that particular crystal is. All other features of that crystal follow in one way or another from this internal structure. The (purely) geometrical pattern of (the location of) crystal constituents is partially dependent on the nature of the atoms, their (chemical) bonds and their size (in fact their radii of influence). One and the same chemical composition can still admit of several different geometrical patterns. The final 'choice' of pattern (i.e. which pattern will finally be adopted by a crystal) depends on some external conditions.
A very important aspect of this final atomic pattern is its symmetry.

A crystal is a periodic arrangement of repeating 'motifs'. These motifs can be atoms, or ions, or certain local configurations of atoms (or / and ions). This atomic pattern can extend itself more or less indefinitely like the pattern of an old-fashioned wallpaper. In Crystallography it is considered as being indefinitely extended. Such a pattern has a certain symmetry.
What does this mean?
The symmetry of a periodic pattern of repeated motifs is the total set of symmetry operations allowed by that pattern. A symmetry operation allowed by a pattern is an operation (like rotation, reflection or translation), that, when applied to that pattern, leaves that pattern unchanged, also with respect to its orientation. When we, for example, apply a rotation of 90 degrees about the center of the pattern

(a pattern which is thought to be indefinitely extended), then this pattern will be unchanged as a result of this operation, i.e. the operation maps the pattern onto itself. Also a linear shift (translation) of this pattern (again thought to be indefinitely extended) by a certain amount (in this case by the length of a small square, or a multiple thereof) results in that same pattern again. The total set of such symmetry operations, applicable to the pattern is, as has been said, the pattern's symmetry, and is mathematically described by a so-called Space Group ( For two-dimensional patterns, like the pattern just mentioned, it is called its Plane Group.). So the Space Group of a crystal describes the symmetry (content) of that crystal, and as such it describes an important aspect of that crystal's internal structure.
A Space Group includes two main types of symmetries (= symmetry operations) :

1. The Translative Symmetries, and
2. The Point Symmetries

Translative symmetries relate to operations that either are themselves linear shifts, or contain such shifts. There are three types of translational symmetry :

• Translation
• Screw axis
• Glide Plane

A second type of translational symmetry (i.e. symmetry operation) is the screw axis.
Having a screw axis means that the structure, possessing one, will cover itself completely after it has been rotated through a specified angle plus being translated (along a straight line, namely along the axis of rotation) over a specified distance.

A third type of translational symmetry is the glide plane.
Having a glide plane with respect to a plane m means that the structure, possessing one, will cover itself completely after it has been reflected in m plus being translated over a specified distance in a certain (translational) direction parallel to m.

But these translational symmetries which involve the movement (shift) of all the points of the structure during the symmetry operation (cover operation), are macroscopically not, just like that, visible because the translation lengths are in the order of 0.00000001 cm. But some effects of these symmetries can become macroscopically visible. For example, possession of either a righthanded screw axis or a lefthanded screw axis in the mineral Quartz, causes the occurrence of enantiomorphic crystal forms, i.e. crystals which are mirror images of each other.

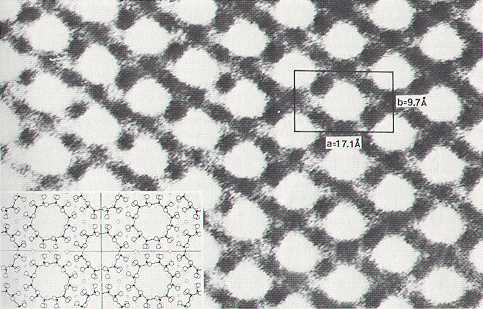
Figure 1. High magnification structure image of an a-b section (i.e. containing the crystallographic axes a and b ) through the mineral Cordierite. An orthorhombic unit cell is outlined and distances are given in Angstroms. The insert shows the idealized structure of Cordierite, as determined by X-ray diffraction techniques. The scales of the idealized structure and the electron transmission image are identical.
( After Hurlbut & Klein, 1977, Manual of Mineralogy )

All the remaining symmetries (symmetry operations) are macroscopically visible. These symmetries occur, together with the translational symmetries, in (all) crystalline matter (crystals). They are the so-called point symmetries. They also are cover operations (symmetry operations), but here at least one point remains where it was, after such an operation has been applied to the crystal. These operations are :

• Reflection in a plane.
• Reflection in a point (= inversion).
• Rotation about an imaginary axis.
• Rotation-and-after-it-inversion (= roto-inversion).

In the case of crystals only the following rotation axes (denoted with a number), with respect to rotational symmetry operations, can occur :

1 (rotation through 360 degrees)
2 (rotation through 180 degrees)
3 (rotation through 120 degrees)
4 (rotation through 90 degrees)
6 (rotation through 60 degrees)

With all these mentioned pointsymmetries (i.e. Rotation, Reflection, and Roto-inversion) combinations can be made, which themselves are again cover operations, and this results in a total of 32 unique possibilities (included the mentioned simple symmetries), i.e. 32 pointsymmetries, and in this way 32 Crystal Classes which are divided among the different Crystal Systems.

The Pointsymmetries are also called Point Groups. The term "group" in "Point Group" and in "Space Group" refers to the mathematical theory, Group Theory, which can describe the symmetries in a formal way and which can deduce theorems. We can discriminate Crystal Systems because some Crystal Classes show similarities among each other and permit some groupings (sets) of them. These groupings are called Crystal Systems. There are six such systems, and each one of them is compatible with the outer form of a certain (repeated) building block :

1. The Isometric System (also called Cubic System)
2. The Tetragonal System (also called Quadratic System)
3. The Hexagonal System
4. The Orthorhombic System
5. The Monoclinic System
6. The Triclinic System

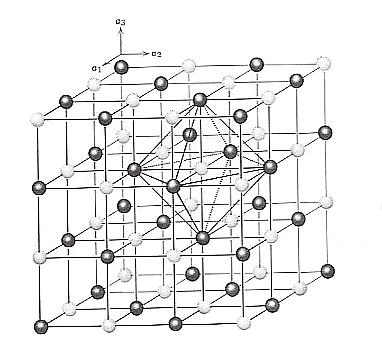
Figure 2. Sodium chloride (NaCl) structure based on two interpenetrating face-centered cubic lattices. Each ion is surrounded by 6 neighboring ions of opposite charge, outlining octahedral polyhedra.
( After Hurlbut & Klein, 1977, Manual of Minerology )

Figure 3. Topaz crystal, Alabaschka, Sovjet-Union
(After CLARK, A., Mineralen (Original title, Minerals), Dutch Edition, ICOB cv, Alphen aan den Rijn)

Ontological Interpretation of Crystals

Crystals are formed either from a solution or from a molten material, or from vapor. In all these cases we have to do with dynamical systems. Such a dynamical system generates one or more crystals. When, for example, we have a solution of a chemical compound then, when certain conditions, such as temperature, concentration of the chemical compound, are satisfied, crystals are formed. If more than one crystal is formed, then we can interpret this in the following way :
At every location where a crystal was formed, the conditions mentioned were satisfied and the relevant crystallization law started to operate. Because such a law is inherent in the interacting (mostly in the form of just aggregating) particles, and because several individual crystals were being generated, we can say that the just mentioned crystallization law is, in its active form, copied along with those crystal individuals. For our purposes it is therefore sufficient to confine ourselves in all cases to one crystal only (out of the many that are generated).
In this way we can consider a crystal as an individual being that is intrinsically ONE, and thus as a First Substance.
The Essence of this individual crystal is the Dynamical Law (the relevant crystallization law) that generated that crystal.
This Essence or Identity abides in the 'genotypical' domain.
The First Substance, with all its properties, abides in the 'phenotypical' domain (See for these concepts Part One of the Essay on Determinations ).

The particular crystallization law generally is either not precisely known, or it is difficult to formulate. This relates especially to our conception of the Dynamical Law. In this conception such a law is fairly abstract (expressed with the above term genotypical ), it resides in certain aspects of the system constituents, and as such is dispersed over those constituents, i.e. one and the same Dynamical Law has its existence rooted not in a single system constituent or a single aspect of such a constituent, but in aspects of many (different) system constituents (elements). Those aspects together make up the one Dynamical Law.
So when we consider the Essence of a crystal, it seems reasonable to look for direct products of the (hidden) Dynamical Law :   its phenotypical effects. In other words we have to look for a set of properties that precisely and exclusively characterizes, or identifies a given crystal. I found out that two properties, taken together, suffice to do the job :

1. The Chemical Composition, and

2. The Space Group.

The Space Group characterizes only the symmetry of the crystal. It follows that with the Space Group the precise 3-dimensional structure is not yet fully given. This structure is co-determined by the chemical composition of the crystal (different structures can have the same symmetry). Also the dimensions, i.e. the absolute lattice point distances are determined by the chemical composition. The chemical composition thus implies structure but not exhaustively :   The same chemical composition can lead to crystals having different Space Groups, so for example the above mentioned minerals Calcite and Aragonite.

So if we want to specify a given crystal, then those two properties are necessary and sufficient.

When we return to our previous examples relating to the chemical compound Calcium Carbonate (CaCO₃), then we can say with respect to this Calcium Carbonate, that there exist two different species of Substance (in the metaphysical sense), i.e. two, with respect to content, different Substances, namely

1. Aragonite, this species manifests itself by the occurrence of Aragonite crystal individuals, and
2. Calcite, this species manifests itself by the occurrence of Calcite crystal individuals.

An Aragonite crystal is thus -- as a first substance - characterized as follows :

1. Chemical Composition :   CALCIUM CARBONATE.

2. Space Group :   Pmcn (complete symbol :   P2₁ / n 2₁ / m 2₁ / a). [See NOTE 1]

A Calcite crystal is thus -- as a first substance - characterized as follows :

1. Chemical Composition :   CALCIUM CARBONATE.

2. Space Group :   R3*c (complete symbol :   R3*2 / c). [See NOTE 2]

In this way it thus is possible to characterize the inorganic (chemical) elements and the chemical compounds in terms of the Substance-Accident Metaphysics. The crystals, interpreted in this way, will serve us well in our effort in understanding the metaphysical state of affairs in the Real World.

When (in relevant cases) the molecules (or atoms, ions and the like) do not (in such particular cases) exist in a crystalline framework, as is the case in molten material, in solutions and gaseous matter, but also in amorphous solids, then of course those molecules (or atoms, when freely existing, or ions, also when freely existing) are each for themselves a Substance (in the metaphysical sense). The gas Methane for example consists of a large number of Methane individuals, the particular Methane molecules, CH₄.
Along these lines we must interpret Water as a large collection of individual Substances (the water molecules), while an ice crystal can be described as ONE individual Substance.

Although relatively strong attraction forces are present between the water molecules -- the so-called hydrogen bonds (quite typical for water) -- those molecules nevertheless can move freely past one another, in contrast with the case in which water, at decreased temperatures, has become ice (and thus crystalline). Because of the just mentioned attraction forces, liquid water has some sort of structure of loosely connected water molecules. But this structure is, besides being tenuous, as far as one knows, not organized, but randomized.

An ice crystal is ONE Substance, because the many molecules of such a crystal are bonded to each other by the attraction forces mentioned -- the hydrogen bonds -- which now are permanent because of the absence of the intense thermical movements of the molecules. The molecules now are ordered into a specific pattern, and this pattern can be described by means of the symmetries and so by means of the Space Group. Thus in the case of ice the constituents of the crystal -- as has been found out -- are molecules, instead of atoms.
Thus the transition from freely existing water molecules to an ice crystal is -- in this interpretation -- a substantial change (in the metaphysical sense, and in contradistinction to an accidental change), albeit of a special sort, because the chemical composition has not been altered, just like the case of an imagined transformation of Aragonite into Calcite.
But often crystallization also directly implies the formation of a chemical compound. The freely existing constituents, for example in a solution, are connected with each other in the crystallization process.
The crystal grows by apposition of the constituents, and in this process energy states play an important role with respect to the stability of the product (Everything in Nature tries to be in a state of minimum energy, which is the most stable state).

With crystals and crystallization processes, all kinds of strange phenomena can take place, like substitution of constituents, twinning, distortion, change of habit, the appearance of temperature modifications etc., which offer much for the gaining of insight in the metaphysical interpretation of inorganic beings. To cite an example : The shape (the outer form) of a crystal may change, (i.e. be different) while the chemical composition and the Space Group (and by consequence the Essence of the crystal) remain identical. This shape thus is a state, a condition, in which the Substance in question can be in. Here we have to do with a genuine Accident (in the metaphysical sense). Being an Accident here means being   per accidens :   because that Accident (here the shape of the crystal) is not equivalent to, and not totally and exclusively dependent on, the Essence (which the fact of the Essence staying the same demonstrates). The shape of the crystal is partially dependent on certain external conditions, and together with that, on the point of time of observation. Those external conditions can be such (for example different concentrations of the crystallizing substance in the vicinity of the growing crystal) that the shape of the crystal has become strongly deformed (distorted), resulting in a shape having a deviating symmetry. This deviating symmetry is, in the case of distortion, expressed by a difference in length of equivalent crystallographic axes (or of equivalent parts of the same axis) contained within the crystal, or, said in other words : (in the case of distortion) equivalent crystal faces can be differently affected. According to the true symmetry content of the crystal (species) -- which is a reflection of the internal structure -- equivalent crystallographic axes (or equivalent parts), insofar as they are contained within the crystal boundaries, should have the same length, and equivalent faces should look the same. But still the internal structure is unaffeced by all this ( Apart from possible local dislocations in the atomic arrangement, which do often occur, but are not related to the discussed deformation of the shape of the crystal.). And because of this also the true macroscopical symmetry content is conserved (i.e. is also not affected) : If we examine such a crystal showing a deviating symmetry of its shape (a deformation), we can still detect its (having its) true macroscopical symmetry which is indicated by some physical properties which are themselves macroscopically detectable.
Crystals also show a habit, which is the characteristic shape of the crystal, characteristic for the species. But although this habit (after it has been changed into another habit) not only (still) - like in distorted crystals -- shows the true macroscopical symmetry content of the crystal species, but also the one that relates to just its shape --- which in this case means : this shape is, in virtue of a change of habit, changed, it is true, but this changed shape does not involve any difference in the lengths of equivalent crystallographic axes (or of equivalent parts of them) as (they are) contained within the crystal, and equivalent faces always are equally affected . So the crystal is not distorted (See Figure 4) --- it (the habit) is not wholly intrinsic, but needs a specification of external condition :   The habit of this crystal when grown under condition C (always) is : H.
So also here we have to do with a property partially dependent on external conditions, but in this case showing a stronger relationship with the crystal's internal structure (and by implication its Essence) than is the case in distorted crystal shapes. So with the habit of a crystal we have a property that is less per accidens than just deformations are.

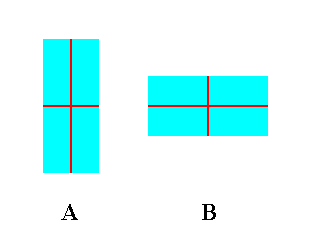
Figure 4. Two different habits (A and B) of a certain crystal species.
Non-equivalent axes remain having different lengths.
Equivalent parts of an axis (i.e. of any axis) remain having the same length.

back to homepage