Crystals revisited

The Structure of Crystals Revisited

Totality Consideration of Crystals

back to homepage

Orientation

In the Essay Crystals and the Substance-Accident Metaphysics we gave a general introduction into Crystals. Later we interpreted Crystals in terms of dynamical systems, resulting in recognizing the crystallization law as the Dynamical Law with respect to the crystal’s generation, and this Law in turn was interpreted as the crystal’s Essence. The visible effect of this Essence is the Chemical Composition + the Space Group of the crystal (under consideration).
A crystal represents an ordered solid state of physical matter. When this matter is still in a gaseous or liquid state it is not ordered (although an intermediary state may occur, the mesophase, namely in the case of liquid crystals (See The Essay Historical Individuum, Here-and-now Individuum, Section Mesophase)).
So the solid state in the form of a crystal is ordered, and the crystal is a Totality, a Substance.

Crystals grow in a melt (= molten mass) or in a solution [ NOTE 1 ], if certain conditions (in such a melt or in such a solution) are satisfied that relate to (1) the nature and concentration of the relevant atomic (ionic-, or molecular) species (concentration = the number of atomic (etc) individuals in a unit of volume), and further (2) the temperature and pressure (thermodynamic conditions).
These conditions accordingly can be such that crystallization sets in. What kind of crystals appears, i.e. what structure actually appears, depends on more special conditions.
Crystals are composed of atoms and/or ions (electrically charged atoms) and/or ionic complexes and/or molecules. Naturally occurring crystals are called minerals. When they are allowed to grow freely they develop faces. Every such crystal is enclosed by a definite set of faces. The occurrence of faces points to a regular internal order. The internal order of crystals is based on an ordered atomic arrangement. This arrangement is moreover periodic. This means that a certain atom (or ion) is present at exactly the same structural (atomic) site throughout an essentially infinite atomic array. An atom at the same atomic site means that it is surrounded by an identical arrangement of neighboring atoms throughout the structure which consists of millions of unit cells (= the unit of structure which is repeated) with dimensions on the order of 5 to 20 Angstrom (1 Angstrom = 10^-8 cm). A unit cell is in fact a basic spatial configuration of some geometrical points (configured into some basic forms like a cube or a parallelepiped). If it is repeated by continual translations (shifts) in three specific directions a point lattice will be formed which represents (i.e. describes) the periodic arrangement of the constituents in a crystal. We can think of the lattice points being occupied, or surrounded, by atoms (ions) or groups of them.
A crystal grows layer by layer by means of accepting certain constituents present in the growing environment (solution, melt or vapor), and in this way extends its lattice. However, the resulting internal periodic ordering (not directly visible macroscopically) is only perfect in 'ideal' crystals. In real crystals imperfections (defects) occur which locally disturb (geometrically) the regular arrangement of the crystal constituents. Such a geometrical disorder may consists in local dislocations. Another kind of imperfection can be caused by chemical zonation of a crystal.

The best way to better understand Crystals, including their nature as Totalities, consists in solving certain problems that pop up in considering them as such.

Substitution in Crystals

One of the problems is the phenomenon of substitution during crystal growth. Substitution does not refer to the replacement of previously (by the crystal) accepted atoms [ NOTE 2 ] by atoms of another species (which can happen at the surface of the growing crystal), but (substitution does refer) to the deposition (apposition) of atoms which do not belong to the presently crystallizing chemical compound [ NOTE 3 ] (which often is present in the solution in a dissociated condition), (a deposition) into places of the progressively extending crystal lattice, (places) which normally would be occupied by atoms of the original chemical compound (See previous Note). So the lattice points of the extending (growing) crystal are occupied by (or associated with) 'alien' atoms (atoms of another species) instead of atoms of the original chemical compound (See previous Note) (See the Essay Historical Individuum, Here-and-now Individuum, Section Metamorphosis).
However such a substitution phenomenon can only take place if the atomic diameters, or, more precisely expressed, the action radii, of the original atoms are almost equal to those of the alien atoms (We should keep in mind that the action radii of different atomic species are never exactly equal). Said differently, substitution is possible if the crystal lattice of the alien chemical compound differs not too much from that of the original compound. And because, as has been said, each atomic species differs in its action radius from any other atomic species, those lattices can never be exactly the same, but some could nevertheless be similar enough for, in the case of substitution, one crystal to be generated.
Such a substitution can take place in two ways :

During the whole period of the growth of the crystal the import of the 'original' atoms and 'alien' atoms could be fifty-fifty (implying of course that in this case there is no true asymmetry between 'original' and 'alien'). In this case a so-called 'mixed crystal' is formed, and more specifically, a homogeneous mixed crystal. The growing crystal accepts without preference 'alien' and 'original' atomic species, resulting in a true homogeneous mixing of them all over the crystal lattice.
During the growth of the crystal initially only 'original' atoms are present in the solution. A (growing) crystal of the original chemical compound is formed. But suppose that at a certain moment 'alien' atoms enter the solution, while the concentration of the original atoms has become very low or even zero (or, if no external agents, exporting those atoms from the solution, were active, the concentration had decreased from supersaturated to saturated in virtue of the crystallization process [ NOTE 4 ]). And suppose that the solution has now become supersaturated with repect to these alien atoms. The growing crystal now accepts these alien atoms (provided them having sufficient similar action radii) because there is nothing else than those. Thus from now on the accretion of particles onto the crystal exclusively consists of atoms of the alien species. Nevertheless the crystal remains one crystal under the conditions mentioned. But we know that the crystal lattices of the respective (chemical) substances must differ, albeit very little. They are not identical. What differs in them for example, are the distances between the lattice points of the original crystal lattice on the one hand, and, on the other, the distances between the corresponding lattice points in the other crystal lattice. We can call such a crystal a zonated crystal (i.e. having layers of different chemical composition). But it is probably more appropriate to call it a heterogeneous mixed crystal (See Figure 1).

In both cases of substitution we have to do with two (or more) chemical compounds (for example Potassium Aluminum Sulfate and Potassium Chromium Sulfate), which nevertheless form one crystal.

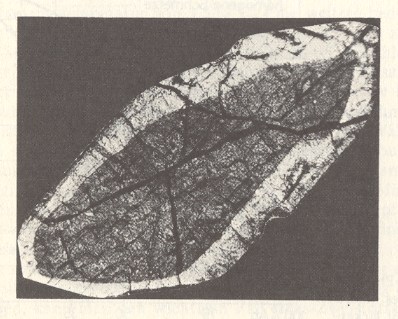
Figure 1. Zone structure in a crystal. Thin slice of a Pyroxene in polarized light. In this case the crystal originated from a melt (molten mass), that has rapidly cooled off. A Pyroxene is a kind of silicate mineral.
(After STRÜBEL, 1977)

What then is the nature of the Totality formed in this way? Is it still a true Totality, or has it perhaps become an aggregate ? And in the second case, should we, when substitution commences, speak of a substantial change, or of only a replacement of one state by another, while the one crystal unfolds? (This question is already discussed in the Section mentioned above on Metamorphosis).
We must try to answere these questions.
Let us start with the second case, the formation of a heterogeneous mixed crystal.

Heterogeneous Mixed Crystals

Now, what exactly happens ontologically (which in the present case is a consideration about being-a-Totality) during this process?
The heterogeneous mixed crystal consists in fact of two (or more) - albeit little - different lattices. This difference expresses a difference in chemical composition. Thus in such a process the Space Group + Chemical Composition (S+C) is changed, because one of it components, namely C, changes into, say, C' (during the formation of the heterogeneous mixed crystal). And because we view S+C as the embodiment of the Dynamical Law [ NOTE 5 ] this Dynamical Law changes as follows :

R+C becomes R+C'

So at first the crystal grows according to S+C, and then according to S+C'. A S+C' process lays itself on top of a S+C process resulting in a zonated crystal. It is clear that this one zonated crystal is an aggregate. In this case an aggregate of two crystals (forming, in a way, one crystal). The degree of being an aggregate is in this case fairly weak, thus implying a situation of it somewhat removed from the aggregate side of the scale Aggregate ------------- Continuum.

The phenomenon of being a zonated crystal, and thus, in a way being one crystal, should be interpreted as just a phenotypical effect, and moreover a per accidens effect : Another Substance (also in the metaphysical sense) just happened to grow on top of the original one, together forming a certain unity because the respective lattices happened to be very similar. The respective Dynamical Laws, and thus the respective Essences, are different nontheless, and this is a genotypical state of affairs.
The second crystal, as it is present in the zonated crystal, has, it is true, the appearance of just a fragment of a crystal instead of a full-fledged crystal, enclosed within its faces, but even as such it is a genuine being, because the opportunity for a crystal to actually develop faces, especially a set of faces that neatly encloses the whole crystal, is per accidens. It depends on the surroundings of the growing crystal whether it can grow freely and develop faces, or not.

Homogeneous Mixed Crystals

This variant of substitution gives rise to a crystal in which the 'alien' and 'original' atoms are evenly distributed within the lattice. Two (or more) chemical compounds are involved that generally differ from each other with respect to one atomic species, for instance Potassium Aluminum Sulfate KAl(SO₄)₂ (common Alum) and Potassium Chromium Sulfate (KCr(SO₄)₂ (Chromium Alum). So here the two differing atomic species are Aluminum (Al) and Chromium (Cr). In the mixed crystal the Chromium atoms occupy those places in the lattice, which would be occupied by Aluminum atoms in the case of a pure Potassium Aluminum Sulfate crystal. A solution containing both Alums will yield mixed crystals because the growing crystal does not discriminate between both atomic species. The crystal accepts both atomic species without preference (HOLDEN & MORRISON, 1982, Crystals and Crystal Growing, p. 36/7). What is formed is accordingly a homogeneous mixed crystal.

There are three reasons to interpret such a mixed crystal as an aggregate, despite the fact that we have to do with (numerically) one crystal. However, in this case not an aggregate of two crystals (thus not an aggregate at the crystal level) but an aggregate of atoms (an aggregate at the atomic level) :

Because the lattices of the two compounds are, (by reason of the difference in atomic action radii of Aluminum and Chromium), not precisely the same, we have to do with a mixture of the two lattices.
The fact that many mixed crystals can demix, indicates their aggregate nature.
A non-mixed crystal (thus a chemically pure crystal) contains atomic species in such a proportion that it reflects the formula of the chemical compound. The pure crystal (the non-mixed crystal) accordingly is one chemical compound. This is not so in the case of a mixed crystal. In the case of the mentioned Alums : The proportion of Cr and Al is wholly extrinsic.

Let us give an (other) example of a mixed crystal and its demixing :
The demixing of high-temperature mixed crystals of (K, Na)AlSiO₃O₈ into :
the mineral Albite, NaAlSi₃O₈, and the mineral Orthoclase, KalSi₃O₈, which (demixing) gives rise to Perthite (STRÜBEL, 1977, Mineralogie, p. 229). The object remains more or less one whole, but now with an alternation between the two components of the mixed crystal.

Figure 2. Perthite, as a result of demixing. Microperthitic demixing of high temperature mixed crystals with chemical composition (K, Na)AlSi₃O₈ into Albite, NaAlSi₃O₈ (light) and Orthoclase, KAlSi₃O₈ (dark).
(After STRÜBEL, 1977)

A homogeneous mixed crystal (and also after its demixing by changed p/t - pressure and temperature - conditions) thus is (from a metaphysical point of view) an aggregate, and in the case of demixing this aggregate shifts still closer to the aggregate side of the scale (true) Aggregate ----------- (true) Continuum :

The homogeneous mixed crystal shows a stronger degree of unity than the corresponding demixed crystal. But this is a phenotypical state of affairs. In the genotypical domain, matters are clear and definite : The mixed crystal and the demixed crystal are each the product of ultimately two definitely specifically different Dynamical Laws (residing in the genotypical domain), and so such a crystal, mixed or demixed, represents two different species of Substance (in the metaphysical sense).
In the case of the homogeneous mixed crystal we should speak of an atomic mixture, an atomic aggregate, but, not at all just like that : The aggregate is organized into a lattice structure, albeit some sort of combination of two slightly different lattices. So as such it comes close to a (i.e. one) genuine being anyway, while its demixed form is just a set of several specifically different crystal individuals (depending on the composition of the original mixed crystal), loosely connected to each other. When seen in a bulky context (as in Figure 2), i.e. as a large set of individual crystals, and assuming that only two substances are involved, we can say that a subset of this set consists of (many) crystals of the one species, while the complement of this set consists of the other species of crystal. And of course all these constituent crystals together form just an aggregate, like we see in many natural rocks. So especially in the case of a homogeneous mixed crystal it is not easy to assess its ontological status, as either a (i.e. one) genuine being, or an aggregate.

Structure, Dynamical Law, Space Group, Chemical Composition and Thermodynamic Conditions

Structure

The direct manifestation of the whatness of a (certain) crystal is its actual structure.
The Structure of a crystal is equivalent to the nature of its constituents and their actual spatial arrangement, including the absolute distances between those constituents.
This structure has the form of (1) a concrete lattice, i.e. a chart of the locations of repeated atomic groupings, and (2) the precise chemical content of those groupings.
It is partly implied by the chemical composition and partly described by the total symmetry content (the Space Group) of the atomic arrangement.

Symmetry

The symmetry of an object is described by indicating the complete set of coincidence operations that are allowed by that object.
A coincidence operation is an operation that, performed on the object, will transform this object into itself.
Point Group and Space Group describe this total of coincidence operations. They are accordingly descriptions (in contradistinction to causes) of the symmetry of an object (See also The Essay Crystals and the Substance-Accident Metaphysics). The Point Group is implied by the Space Group.

Point Group

A Point Group describes the symmetry of an object insofar as only those coincidence operations are involved in which at least one point of the object remains in place during the execution of such a coincidence operation. Examples are Reflection and Rotation, in contradistinction to a translation (= linear shift) in which not any point remains in place. So a Point Group of an object describes the total of non-translative symmetry operations that the object allows [ NOTE 6 ].
With respect to Crystals there are only 32 Point Groups at all possible (the 32 Crystal Classes).

Space Group

The Space Group also describes the symmetry of an object, i.e. describes the total of symmetry operations allowed by the object, but now including all the executable translative coincidence operations (with respect to that object) as well. In the case of a translative coincidence operation not any point remains in place, all the points are displaced, but the object, when considered infinitely extended in space, will coincide with itself. An example is a (linear) shift (of a regular point pattern in a certain direction and along a certain distance).
If we imagine a crystal to be indefinitely extended in space, then crystals exhibit several translational symmetries, meaning that when we subject it to certain translational operations, then the result is a coincidence of the (internal) crystal pattern before and after the operation.
This translative symmetry (aspect) is however only microscopically demonstrable, because the translation distances (i.e. the repeat distances of atoms) are very small [ NOTE 7 ]. For crystals there are in principle 230 Space Groups possible. If we subtract the translative symmetries from a Space Group, then we end up with the corresponding Point Group.
The Space Group (and by implication also the Point Group) all by itself consequently does not directly describe the complete structure of the crystal lattice but exclusively its symmetry, namely the complete symmetry of the crystal lattice considered to be provided with motifs, motifs, representing the (point) symmetry of the constituent atomic configurations that are repeated throughout the crystal. The Space Group does not describe the constituent atoms, but it does describe the total lattice symmetry caused by them. So these atoms, in the form of the Chemical Composition of the crystal, cause (in contradistintion to describe) this symmetry, but not only the crystal’s symmetry, they also cause the complete structure (including the relevant distances between the lattice points) of the crystal lattice [ NOTE 8 ]. But the conditions during growth, like temperature and pressure, are also determining, which implies that one chemical substance can nevertheless give rise to several different crystal forms.

Implicit and Explicit Description

The characterization of a crystal, i.e. the (potentially) complete description of all per se features with respect to that crystal, can be done by means of its Chemical Composition + Space Group. Such a description is to be sure complete, but not wholly explicit.
As has been said, the Space Group exclusively specifies the (complete) symmetry aspect of the relevant lattice as it is (when) provided with motifs, and it does so explicitly. It does, however, not describe the different absolute distances between the lattice points or between the atoms for that matter, neither does it describe the absolute angles between the relevant chemical bonds within the crystal (The distances and angles are implied by the crystal’s chemical composition). So the Space Group does not describe structure. The distances are directly dependent on the chemical composition (namely on the action radii of the relevant atoms), but are - by mentioning just the chemical composition - only implicitly given.
A completely explicit description of all per se features of the crystal should specify the crystal lattice (under consideration) quantitatively, and then indicate which lattice points are occupied by (or associated with) which atoms (ions or molecules).
The significatum (= that to which reference is made) of both types of descriptions, taken together, is the 'fixed kernel' of the crystal, its actual structure, a kernel which doesn’t change during the growth of the crystal. So it is 'concurrent' with its Dynamical Law.
The Dynamical Law is the most implicit (and so most compact) characterization of the crystal by means of a very implicit description of all per se features of the crystal. These per se features are the per se determinations, and these are implied by the Dynamical Law, in the sense of : generated. They are however not identical to the Dynamical Law. The latter is the relevant crystallization law, prevailing during the origin and growth of the crystal.
A precise formulation of the Dynamical Law of one or another crystal is generally not directly possible, but the importance of the introduction of this concept consists in its emphasizing the regular course of real processes, and this means that such a process is deterministic and in principle repeatable. So the concept of Dynamical Law emphasizes the fact that the crystal is a product (a stadium or state) of a dynamical system, and as such it denotes the Essence of the crystal.

Thermodynamic Conditions

Also the external conditions of pressure and temperature (p/t), thus the thermodynamic conditions, are co-determining the crystal structure, which is generated under those conditions. These thermodynamic conditions relate to energetic circumstances. The crystal structure itself represents an energy state in which the whole of constituent particles in a crystal finds itself. It is a state of lowest energy.
Thus Calcium Carbonate, CaCO₃, under certain p/t conditions crystallizes in the form of the mineral Calcite, with Point Group 3*2/m and Space Group R3*2/c [ NOTE 9 ], while under different p/t conditions it crystallizes in the form of the mineral Aragonite, with Point Group 2/m 2/m 2/m and Space Group P2₁/n 2₁/m 2₁/a (STRÜBEL, 1977, p. 424, BURZLAFF & ZIMMEREMANN, 1977, Kristallographie, Band I, Symmetrielehre, pp. 171).
So within the one p/t condition range the one Dynamical Law is triggered into action, while within the other p/t condition range the other Dynamical Law is triggered. So a crystallization law (Dynamical Law) has a limited range of validity, i.e. it only operates within a certain range of external conditions. This range of external conditions wholly relates to the energy condition of the relevant particles taking part in the crystallization. Thus the Dynamical Law is partly contained in these p/t conditions, but these p/t conditions in turn are contained in the particles themselves (Here including their state of motion). Temperature and pressure are statistical quantities which can be reduced to the energy conditions of the individual particles and with it to their state of motion. So the Dynamical Law remains immanent with respect to the particles involved in the crystallization, and in this respect the p/t conditions are not external.

A same chemical composition can accordingly be connected with different Space Groups (and even already with different Crystal Classes (Point Groups)), when we have to do with different p/t conditions.
So the compound Al₂SiO₅, Aluminum Silicate, occurs in three different mineral species (and thus in three different crystalline forms) :

Mineral	Chemical Formula	Crystal Class (Point Group)	Space Group
Andalusite	Al₂SiO₅	2/m 2/m 2/m	P 2₁/n 2₁/n 2/m
Sillimanite	Al₂SiO₅	2/m 2/m 2/m	P 2₁/n 2₁/m 2₁/a
Disthene (= Kyanite)	Al₂SiO₅	1*	P 1*

(See STRÜBEL, 1977, p. 217)

Here we see the necessity of including the Space Group component in the per se description of a crystal. We also see that the mineral Aragonite (chemical composition : Calcium Carbonate) and the mineral Sillimanite (chemical composition : Aluminum Silicate) have the same Space Group (and even the same Point Group), so also the Chemical Composition component is indispensable for the per se description.

In chemically similar chemical compounds we still find differences in their crystal structure, even when the symmetry of the lattices is exactly identical. These differences consist in, for example, length proportions between the a-axis and the c-axis (STRÜBEL, 1977, p. 173) :

Mineral	Chemical Formula	a : c	Crystal Class (Point Group)	Space Group
Calcite	CaCO₃	1 : 0.854	3*2/m	R3*2/c
Rhodochrosite	MnCO₃	1 : 0.818	3*2/m	R3*2/c
Siderite	FeCO₃	1 : 0.814	3*2/m	R3*2/c
Smithsonite	ZnCO₃	1 : 0.806	3*2/m	R3*2/c
Magnesite	MgCO₃	1 : 0.811	3*2/m	R3*2/c

Here we see the necessity of including the Chemical Composition component into the the per se description.
Chemical Composition + Space group reflects accordingly the Dynamical Law, which operated during the growth of the crystal.

The concept of Dynamical Law has been related to the the per se characterization of a crystal in the form of : Space Group + Chemical Composition.

However one has synthesized crystals, the so-called Pseudo Crystals, in which the 5-fold symmetry, 'forbidden' for crystals [ NOTE 10 ], nevertheless occurs (In organisms this 5-fold symmetry is wide-spread). This implies that the inner structure, resulting in them, is not periodic in its nature (STEWART & GOLUBITSKY, 1993, Fearful Symmetry, Is God a geometer? p. 95/6, and BALL, 1994, Designing the Molecular World, Chemistry at the Frontier, pp. 122).

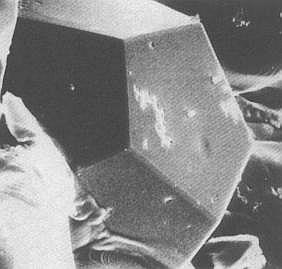
Figure 3. A Pseudo Crystal. These can have
shapes that reflect the forbidden symmetries
of the atomic structure. In this picture, the
pseudo crystal has a dodecahedral shape.
(After BALL, 1994)

This discovery could perhaps imply that the current Group Theoretical Paradigm (expressed with the concepts of Point Group and Space Group) is not necessarily all there is to say about crystal structure (STEWART & GOLUBITSKY, 1993, p. 96).

Looking again to the aforementioned system of Al₂SiO₅ we see that it is, from a chemical perspective, one system, which can give rise to several mineral phases : Andalusite, Sillimanite and Disthene. Each for themselves these phases are stable in a definite region of the Triple Point Diagram (STRÜBEL, 1977, p. 217) , which has two axes, the temperature axis and the pressure axis. So here we have the (one) system of Al₂SiO₅, with three mineral phases, and only at the Triple point all three mineral phases can co-exist. Of course not in a stable way.
Hoewever, within our Totality Consideration we have to do with three systems, because in such a consideration the crystals are central. Accordingly in this case we have to do with three Dynamical Laws (crystallization laws), and their respective domains of validity are given in the Triple Point Diagram.

Aggregates

The fact that minerals can form strange types of aggregates (or weak Totalities), can be illustrated by three examples, Opal, Wavellite and Rutilated Quartz.

Opal, SiO₂ . n H₂O

Although Opal is essentially amorphous, it was demonstrated that it nevertheless has an ordered structure. It is however not a crystal structure with atoms in a regular 3-dimensional array, but consists of closely packed silica spheres in hexagonal and / or cubic closest packing. Air or water occupy the spaces between the spheres.

Figure 4. Scanning electron micrograph of an OPAL with chalky appearance showing hexagonal packing of silica spheres (diameter of spheres approximately 3000 Angstrom (1 Angstrom = 0.00000001 cm). Because of the weak bonding between the spheres they are completely intact. Here we have an example of an aggregate wich is almost a Totality, although the pattern is not very elaborate, it is just a dense packing of weakly bonded spheres, wich are themselves probably more stronger Totalities (consisting of SiO₂ + Water).
( After Hurlbut & Klein, 1977, Manual of Mineralogy )

In ordinary Opal the regions of equally sized silica spheres with uniform packing are small or non-existent, but in precious Opal large regions are constituted of regularly packed spheres of the same size. The diameter of the spheres varies from one Opal sort to the other, and ranges from 1500 Angstrom to 3000 Angstrom (1 Angstrom = 10^-8 cm) (HURLBUT & KLEIN, 1977, Manual of Mineralogy, p. 419).
Opal can, according to me, best be interpreted as an aggregate, albeit not situated at the very aggregate end of the scale Aggregate ----------- Continuum.
An Opal does not, as it seems, have an intrinsic interface with the environment (= the surroundings of the Totality - or pseudo Totality), yet another ground for interpreting it as an aggregate.

Wavellite, Al₃(PO₄)₂ (OH)₃ . 5 H₂O

Some minerals preferably form structured crystal aggregates, for example Wavellite (HURLBUT & KLEIN, 1977, p. 333 ; STRÜBEL, 1977, p. 343).
In the case of Wavellite individual crystals, i.e. free crystals, are rare. Usually it occurs in the form of radiating spherulitic and globular aggregates.

Figure 5. Wavellite from Dünsberg near Giessen (Germany)
(After STRÜBEL, 1977)

Wavellite crystallizes in the Orthorhombic Crystal System in the Crystal Class (= Point Group) 2/m 2/m 2/m, and has as Space Group Pcmn (abbreviated symbol).
So in the case of Wavellite we have to do with ordered aggregates of crystals, having a more or less intrinsic (spherical) interface with the environment, and accordingly they are, as such - be it weakly expressed - Totalities, and each for themselves (they are) a Totality of a higher scale order than is the individual Wavellite crystal. However it could be that the structuring of the aggregate has external causes, although the fact that Wavellite usually occurs in the form of such aggregates (i.e. seldom in the form of individual free crystals) speaks against this.

Radiating crystal aggregates are also formed in Zeolites, for example Natrolite, and also in Limonite, Malachite and Antimonite.

Rutilated Quartz (Rutile, TiO₂, Quartz, SiO₂)

Also crystals within crystals do occur in Nature, for example Rutilated Quartz. This is Quartz which has fine needles of Rutile penetrating it.

Figure 6. Rutilated Quartz, Brazil
(After HURLBUT & KLEIN, 1977)

This we should interpret as an aggregate, although a more or less weak form of it. In this case it is an aggregate of two different crystal species, Quartz and Rutile.

Pseudomorphosis

It sometimes occurs in Nature that crystals dissolve in a special way : the original chemical substance will be replaced by another material while the form of the original crystal is preserved. So it can happen that Barite (BaSO₄) dissolves, because of changed pressure and temperature conditions in salty water. The BaSO₄ is abducted and in its place Quartz (SiO₂) is precipitated. With it the outer form of the Barite crystals is preserved. One calls this phenomenon a pseudomorphosis of Quartz to Barite.
Here we have an entity having a definite and specific boundary, but this boundary is not related to its content. The Quartz is formed within a special cavity which is however per accidens with respect to it.

Paramorphosis

Paramorphosis is a phenomenon analogous to pseudomorphosis, but in this case there is no change in chemical substance. What changes is the inner structure, while the outer form remains the same. For example when high-Quartz cools until below 573 degrees Celcius, trigonal low-Quartz is formed, which could however preserve the outer hexagonal form of the high-Quartz.
The transformation of high-Quartz into low-Quartz and vice versa (with or without accompanying paramorphosis) is a so-called displacive polymorphic reaction (See Figure 7). It consists in an internal adjustment which is very small and requiring little energy. The structure is generally left completely intact and no bonds between ions must be broken, only a slight displacement of atoms (or ions) and readjustment of bond angles ('kinking') between ions is needed. This type of transformation occurs instantaneously and is reversible. The difference between the two forms of Quartz is expressed by their Space Groups, low-Quartz, P3₂21, high-Quartz, P6₂22. The structural arrangement in the low-temperature form is slightly less symmetric and somewhat more dense than that of the high-temperature form (HURLBUT & KLEIN, 1977, p. 151). So this transformation is a very slight one indeed. Nevertheless it results in a different Space Group. Consequently in our ontological interpretation of crystalline chemical substances the change is a substantial change, because the Chemical Composition + Space Group is changed (in virtue of the change in one of its components). So even in the case when this process is moreover accompanied by paramorphosis (i.e. the preservation of the outer form), it is a change from one Substance (in the metaphysical sense) into another.

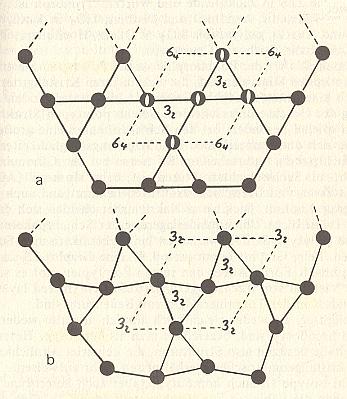
Figure 7. Lattices of low-Quartz (bottom) and high-Quartz (top).
Projection of the lattices in the direction of the c axis.
When paramorphosis occurs the outer form of high-Quartz is preserved after
its transformation into low-Quartz.
All the 6-fold screw axes ( 6₄ ) of high-Quartz become 3-fold screw axes ( 3₂ ) after
its transformation into low-Quartz.
The black disks represent Silicon ( Si ) atoms. The unit cell is outlined by dashed lines.
Its vertices are lattice points. Compare with Figure 9.
(After STRÜBEL, 1977)

Formation of Crystal Lattices

When the atoms in a melt or in a solution do not move too fast anymore (when, say, the temperature falls), they’re going to attract each other strongly. However, when they, in virtue of this attracion, are coming too close to each other, short range repelling forces come into being. The system (always) strives to be in a lowest possible potential energy condition of those atoms, i.e. of the constituents of that (crystallization) system. While subjected to an attractive force, for the atoms to be far from each other means that they then have a high potential energy (which, in the case of the atoms, approaching each other, will be transformed into kinetic energy, i.e. energy of motion). So on approaching each other the potential energy of the relevant atoms decreases. But while subjected to a repelling force, for the atoms to be nearer to each other means that they have potential energy. When they then move apart this potential energy decreases (it is transformed into kinetic energy).
So there exists a definite distance - a distance between the atoms - where the potential energy of those atoms is minimal. Such a condition of minimal potential energy is the most stable state, and hence a system of atoms - supposing that their velocities have become low - will tend to reach such a state.
It is almost certain - but not yet strictly proven - that the particles, in order to find themselves in such a condition of minimal potential energy, arrange themselves into a lattice (instead, for example, to distribute themselves randomly). If this is indeed correct then the lattices of crystals are a direct and necessary effect of the 'desire' to be in a condition of minimal potential energy. A lattice is a periodic arrangement. That is an arrangement such that in it a smallest unit [ NOTE 11 ] (the so-called unit cell) can be found which keeps repeating itself in three directions. We can imagine that we set up the lattice by repeating a unit cell along three directions, namely by a repeated linear shift (translation) of that unit cell. In this way (now considering such a repetition only along two directions) the stable packing of a layer of identical spheres, distributed over a planar surface, assumes the form of a (2-dimensional) hexagonal lattice, which looks as follows :

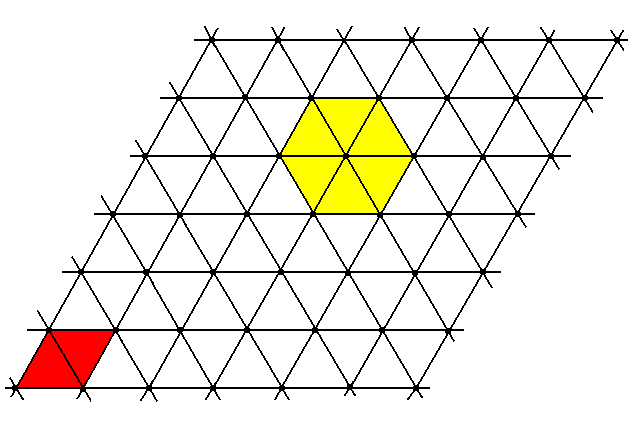
Figure 8. Two-dimensional hexagonal point lattice.
The nodes in the figure represent the points, and these in turn represent the centers of the packed spheres. The unit cell is a rhombus (red). The hexagonality is indicated by yellow coloring of a part of the lattice.

Something similar will be the case with the packing of atoms. And also a three-dimensional packing of them.
But why then aren't all crytstal lattices hexagonal? Well then, lattices of a different nature could be most favorable arrangements when several different atomic species are involved, thus in the case of crystallization of a chemical compound (of several different atomic species). Moreover, even identical atoms could exert forces on each other of different strenght in different directions, and this lets them pack together in different ways, resulting in different lattices.
For a three-dimensional packing of identical spheres it is proven by Carl Friedrich GAUSS that among lattice-packings the face-centered cubic ordering is the best (A face-centered cubic lattice is an arrangement with a (repeating) unit cell having the form of a cube of which not only the vertices but also the centers of the faces are occupied by lattice points). And that means : as much -- each other not penetrating -- spheres as possible in as little a volume as possible, and that is accordingly energetically the most favorable packing. Not yet strictly proven is that the best packing is a lattice at all. It will sound improbable that one or another irregular mess of spheres could fill space better than a regular arrangement, but it is not self-evident how such an assertion could be proven. According to STEWART & GOLUBITSKY, 1993, it is even incorrect for packings in a 1000-dimensional space, where arbitrary arrangements can fill space better than any lattice whatsoever.
But let us limit ourselves to 3-dimensional space, thus to 3-dimensional crystals.
The crystal structure, hence the crystal lattice, is, with respect to its geometry, dependent on just a certain aspect of the chemical composition, in that sense that the originating structure of the crystal lattice is indifferent to many other aspects belonging to the chemical composition. Only the inclination towards an energy minimum, combined with the action radii of atoms (their 'sizes'), plays a role in the lattice formation. The remaining aspects of the identity (i.e. those aspects causing their allocation to a species) of the participating atoms do not play any role. That’s why lattice structures can appear everywhere, also totally outside the domain of crystals.

The crystal lattice represents the internal structure of a crystal. This structure is an ordered structure. In Nature there are many ordered structures. Some of these ordered structures are periodic, and it is this type of ordering that we encounter in crystals. It can be described with a three-dimensional lattice. A lattice is an abstract geometrical concept (as has been said, in order to describe the structure of a crystal). A lattice is accordingly a three-dimensional periodic ordering of points. In real crystals these lattice points can be occupied by atoms (ions, ion complexes or molecules). But such a coincidence of geometrical lattice points with (positions of) atoms is not compelling. Often they do not coincide. The lattice points are just geometrical points in the structure which all have the same angle and distance relations to the atoms that compose the crystal, and with it to the symmetry elements [ NOTE 12 ] of the crystal structure. Every lattice point is equivalent to every other lattice point. So every lattice point is associated with a same atomic pattern (sometimes this pattern consists of only one atom). The point lattice only indicates the way (i.e. the directions) of repetition of these atomic patterns, and also the distances between the repeated units. Surely each lattice point always represents the location of a motif, i.e. a pattern of atoms of which the geometrical center, or another representative point, coincides with a lattice point. If this motif consists of only one atom then the position of that atom coincides with the relevant lattice point. The geometrical lattice points reflect and represent accordingly the relevant periodic ordering of the crystal constituents (See KLEIN & HURLBUT, 1999, Manual of Mineralogy, p. 129, and especially the next figure).

Figure 9. A drawing of the structure of low (alpha) Quartz ( SiO₂ ), with the normally vertical z axis tilted at a small angle to better show the repeat distance c (of the unit cell) along the z direction. The primitive hexagonal space lattice [ NOTE 13 ] , outlined by the various parallelepipeds, shows that each unit cell (with edges a₁ , a₂ and c) contains a complete and representative unit of the repeating pattern of the structure. Large circles are Oxygen atoms (O), small circles are Silicon atoms ( Si ).
(After KLEIN & HURLBUT, 1999)

If we compare the above figure with Figure 8, then we clearly recognize the hexagonal arrangement of lattice points. We also see the chemical bonds and their directions (four bonds -valencies - for Silicon, two for Oxygen). Moreover it is clear from the picture that the point lattice is purely geometric in nature, describing the repetition of material units.

In most cases the points of the crystal lattice are, as has been said, each for themselves occupied by a pattern of several atoms. This pattern will then, in accordance with the geometry of the lattice, be repeated. The actual chemical structure of the crystal, thus the bonding of the individuals atoms to each other, forming for example SiO₄ tetrahedrons [ NOTE 14 ], is not displayed by the lattice structure. The lattice structure only displays, as has been said, the nature of the periodic ordering of the crystal constituents. Of course there is a dependence relation between the chemical bonds on the one hand, and the lattice to be formed on the other. The next figure will make this clear.

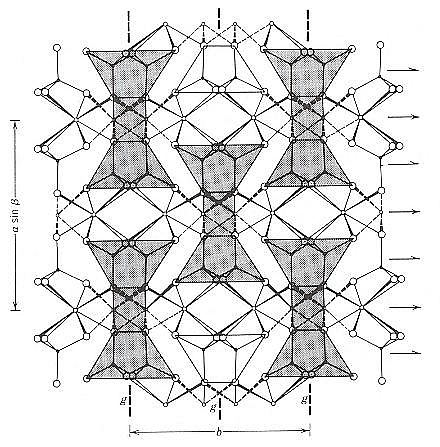
Figure 10. A view of the clinopyroxene structure along the c axis. The shaded parts identify repeats of some of the motifs in the structure. These structural units are repeated in a centered pattern in this view, i.e. four motifs at the corners and one in the center. In three dimensions this is compatible with a C-centered monoclinic lattice (denoted as C). So the geometrical centers of the motifs are the lattice points.
(Two types of) arrows indicate the location of 2-fold rotation axes and 2-fold screw axes - the latter as a result of the centering.
(After KLEIN & HURLBUT, 1999)

Also the next three figures, displaying the mineral Beryl, Be₃Al₂Si₆O₁₈, will show the relationship between the actual internal structure of a crystal of this mineral and the crystal lattice, describing the way of repetition of structural units.

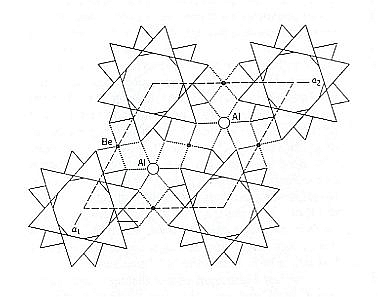
Figure 11. The structure of Beryl as projected onto (0001), i.e. projected onto the base face of the crystal. A unit cell is shown by dashed lines. The unique 6-fold Si₆O₁₈ rings are shown. In fact we see four pairs of such rings, each pair consisting of two rings (separated by other structural elements) in alternating orientation. Of course this whole structure keeps repeating itself.
If the centers of four of these rings are chosen as the positions for possible lattice nodes (points), the rhombus shape of the lattice becomes obvious, and this corresponds to a primitive hexagonal lattice choice. A two-dimensional version of such a lattice was pictured in figure 8.
If we repeat the unit cell of the Beryl structure several times, then we get the next Figure, in which the hexagonal arrangement becomes clear.
(After KLEIN & HURLBUT, 1999)

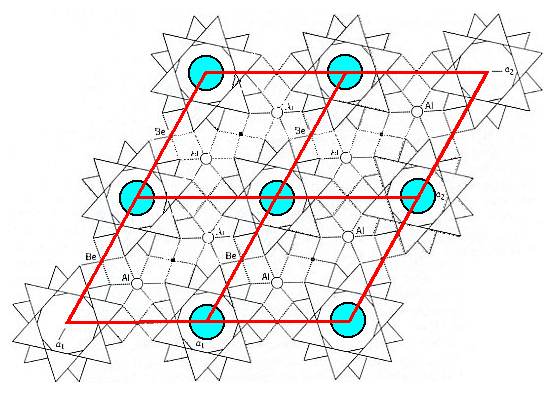
Figure 12. Structure of Beryl. Obtained by repeating the unit cell outlined in Figure 11, in order to show the hexagonal lattice.

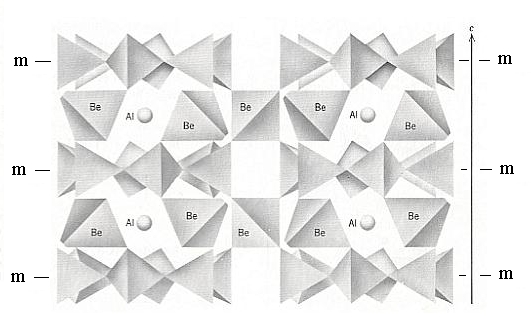
Figure 13. A vertical three-dimensional view of the Beryl structure. The location of horizontal mirrors through the centers of the rings is shown ( the hexagonal outline of, and horizontal mirrors through these rings account for 6/m in the Space Group symbol, which is P 6/m 2/c 2/c ). Be (Beryllium) and Al (Aluminum) provide cross-links between the Si₆O₁₈ rings.
(Adapted from KLEIN & HURLBUT, 1977)

Further it is important to realize that the presence of glide planes and screw axes [NOTE 15 ] often has the status of being introduced in virtue of the choice of a unit cell. In Space Groups with a lattice which (because of the choice of unit cell) is not primitive, i.e. with centering [ NOTE 16 ], screw axes and glide planes are introduced because of the centering. These new symmetry elements are not included in the Space Group symbols (because they are implied). So in the case of non-primitive lattice types one should be aware of this (KLEIN & HURLBUT, 1999, p. 139).

Point Lattice and Space Group

It is important to distinguish clearly between point lattice and Space Group.
A point lattice is a homogeneous infinite (at least in principle) array of points. These points are related to each other by linear translations, in such a way that all the points are equivalent, they all have the same neighborhood. As such it can be interpreted as the repetition, not only of points but also of some basic pattern of some of these points, the unit cell. For three-dimensional patterns 14 unique point lattices are possible, i.e. they represent the only possible ways in which points can be arranged periodically in three dimensions. They are called the 14 Bravais lattices. Their symmetry depends on the symmetry of their respective unit cell, and can be described by a Space Group and represented by a Space Group symbol. As long as the unit cells are just patterns of points, for example eight lattice points forming a cube (which, as unit cell keeps on repeating itself in three directions), the symmetry of the lattices is the highest possible (i.e. the highest possible for each lattice type).
As soon as we superimpose compatible [ NOTE 17 ] motifs (which could be atoms or atomic complexes) onto the point lattice (in which case its points are now related to the location of the motifs), the symmetry of the resulting pattern of periodically repeated motifs can be either the same as that of the original point lattice, or be lower. The former is the case when the symmetry of the (identical) motifs is the same as that of the original unit cell of the given point lattice. If the symmetry of the (identical) motifs is lower, then, also the resulting pattern of periodically repeated motifs has a correspondingly lower symmetry. The total symmetry of the pattern of repeated motifs is again described by a Space Group (The total symmetry of two-dimensional periodic patterns is described by the so-called Plane Groups).
Important for us is the fact that Space Groups do, it is true, account for motifs, but only insofar as their symmetry (point symmetry of the motifs) is concerned. Motifs with the same (point group) symmetry can nevertheless be very different. So the actual structure of, say, a crystal is only partly implied by its Space Group. The rest will be implied by (information about) the chemical composition. The information about the chemical composition could consist in (giving) its structural formula unit, for instance CaB(SiO₄)(OH) (= Datolite).

Because the Space Group is an essential part of the total effect of the Dynamical Law of the crystal (i.e. the total symmetry content of a crystal -- which is that essential part -- is generated by that particular Dynamical Law), we will elaborate a little more on the concept of Space Group, and of the related concept of Point Group.
The Point Group of a crystal is the translation-free residue of its Space Group, i.e. if we consider the total symmetry content of a crystal, and then eliminate all translational symmetry, then we end up with the Point Group of that crystal. Translational symmetry itself is not macroscopically visible, so what is left after its elimination is the macroscopically visible symmetry, expressed, among other things, by the shape of an undisturbed crystal (i.e. a crystal that grew freely under homogeneous conditions), the physical (and geometrical) equivalence between certain crystal faces, their arrangement with respect to certain directions (crystallographic axes), and so on. How do we mentally accomplish the just mentioned elimination of all translative symmetry? We can do this by mentally superimposing all motifs (atoms, or clusters thereof) of the lattice, resulting in one final motif. The (point) symmetry of this one motif then represents the point symmetry of the crystal, expressed by its Point Group.
The internal order causes the basic morphology of the crystal. Hence its Point Group can be derived from its Space Group.
So the Space Group governs the Point Group of the Crystal. It moreover governs the point symmetry of the individual motifs, and also the point symmetry of motif units, i.e. of parts of the motifs. Finally it governs the orientation of the motifs in the translational lattice, or, equivalently, it governs the orientation of the translational lattice with respect to the motifs which are placed in it. So the Space Group controls everything that has to do with the symmetry properties of a crystal. And, as has been said on many occasions, if we supplement the information about the Space Group to which a crystal belongs with information about its chemical composition, then the structure of the crystal is completely determined. This structure is the direct 'phenotypical' expression of the relevant Dynamical Law.

In all this we see that the structure of crystals is not a simple matter. In many cases we have to do with several lattices which are placed within each other, thus a structure in which several lattices penetrate each other. Let all this, as said, be complicated. Compared with Organisms Crystals are however very simple.

For a more extensive treatment of the internal structure of crystals (making much use of the two-dimensional analogues of (3-D) crystals), see the Essay on The Internal Structure of Crystals, Part I ---- Part XX.

In the next Essay of this Series, namely the Essay on The Morphology of Crystals, we will treat of the macroscopical features of Crystals, especially their macroscopic symmetry elements, constituting their Point Groups.

back to homepage

****************