back to homepage
The External Shapes of periodic 2-D arrays of repeated two-dimensional motifs
Oblique Net.
The 2-D Oblique Crystal System (which is based on the Oblique Net) has two Classes, each having only one Plane Group. The first (most symmetric) Class (2) -- to which only the Plane Group P2 belongs -- was discussed in the previous Part, with respect to the possible faces, Forms and combinations of Forms. In the present Part we will discuss the other Class (1) to which only the Plane Group P1 belongs.
Recall that a (2-D) Crystal Class only refers to the point symmetry of the relevant (2-D) crystals, i.e. the translation-free residue of their total symmetry, while the Plane Group refers to the total symmetry of those same crystals, i.e. includung translational symmetry elements (in the 2-D case : simple translations, and glide lines).
The faces, Forms and combination of Forms are based on the same net as those of the Class 2 discussed earlier (See Figure 1 of the previous Part). So also the set of crystallographic axes (See Figure 2 of the previous Part), to which the orientations of the faces are referred.
The present Class being 1 implies that the point symmetry of the 2-D crystals to be constructed is 1, which means that they have no point symmetry at all. It is the asymmetric Class of the 2-D crystals. So if a face is initially given it will not be multiplied by any symmetry element, because there are no genuine symmetry elements involved. This means that every possible single face is at the same time a Form. The periodic stacking of (empty) building blocks (the meshes of the net) determines which faces are possible and which are not. A face is a possible face if it can be built by stacking one and the same building block in a periodic way, i.e. without turning them while they're being stacked.
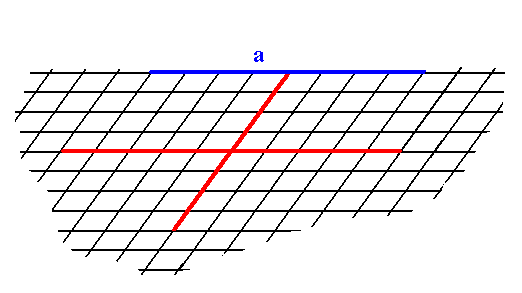
To begin with, we insert a possible initial face -- in the present case one that is parallel to one of the crystallographic axes. Because there are no symmetry elements, the face, all by its own, is already consistent with 1 point symmetry, so no further faces are implied by this initial face, it is at the same time already a possible Form of the Class. See Figure 1.

Figure 1. A possible face (a), supported by the oblique net. Because it should be a face of a crystal belonging to the asymmetric Class, no new faces are implied by it, and it is therefore at the same time a possible Form of the Class.
As is evident it is an open Form, and can only be imagined to exist in 2-D crystals when combined with other Forms of the same Crystal Class such that a closed configuration of faces appears.
Another possible face (Form) is depicted in the next Figure.
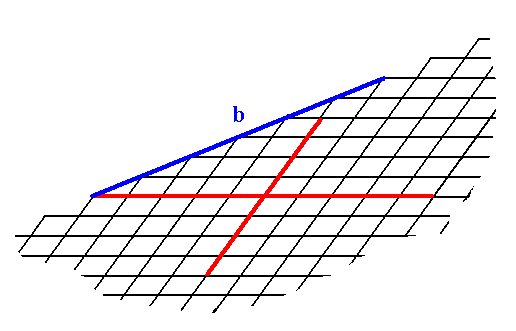
Figure 2. A possible face (Form) (b) in the 2-D Crystal Class 1.
By combining possible faces (Forms) one can construct a 2-D crystal belonging to Class 1. See Figures 3, 3a and 3b.
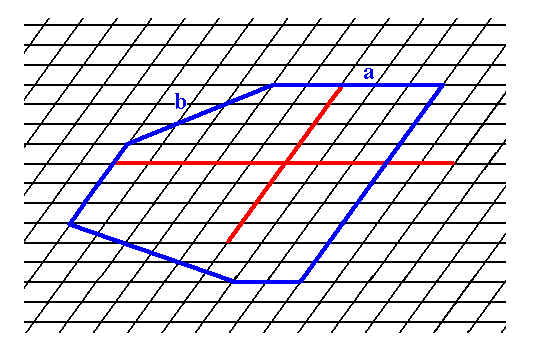
Figure 3. Construction of a 2-D crystal based on an oblique net and on the point symmetry that it should possess. We have used the face (Form) a of Figure 1 (two times), the face (Form) b of Figure 2 and two more other possible faces (of which one is used twice). The continuation of the construction is depicted in the next Figure, and the final result is given in Figure 3b.
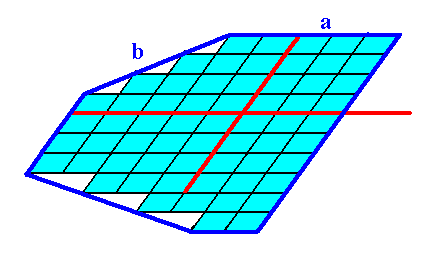
Figure 3a. Continuation of the construction of the 2-D crystal.
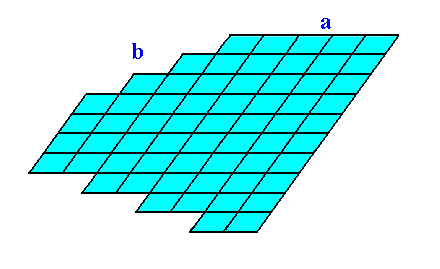
Figure 3b. Result of the construction of the 2-D crystal as specified above, belonging to the 2-D Crystal Class 1 of the 2-D Oblique Crystal System.
The next Figures depict the different atomic aspects (as represented by motif configurations) to the growing environment of some of the above discussed possible faces (Forms).
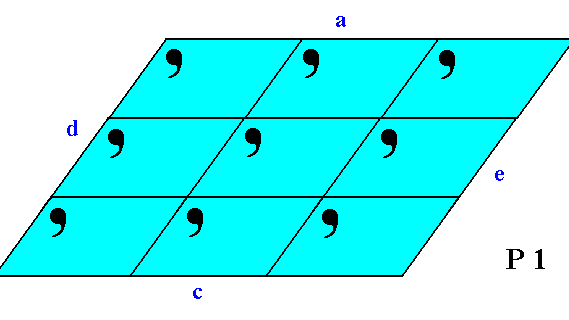
Figure 4. The four faces a, c, d, e present a different atomic aspect to the growing environment of the crystal. So although the faces a and c are parallel to each other they present a different aspect to the environment, so they are not equivalent. The same goes for the faces d and e. And although the external shape of the 2-D crystal suggests symmetry to be present, we can see -- when concentrating on the content of the crystal -- that there isn't any symmetry present.
It is interesing to compare this crystal with one of those discussed earlier. It is a crystal also belonging to the 2-D crystal system, but in another Class of that system, namely Class 2. This crystal has precisely the same external shape as the one of Figure 4, but the latter has no point symmetry at all, while the former has a 2-fold rotation axis representing its point symmetry. The difference between the two crystals can be detected from their internal content, and consequently from the different aspects they present to the growing environment.
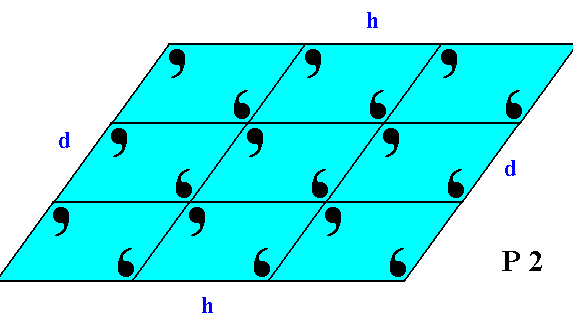
Figure 4a. A 2-D crystal of Class 2 of the 2-D Oblique System.
It has the same external shape as the one in Figure 4, which is a crystal of Class 1. The atomic aspects they present to the environment are, however, different, causing the non-equivalence of faces in the case of the crystal of Figure 4. In the crystal of the present Figure the faces d, d are equivalent, because they are presenting identical aspects to the environment. The same goes for the faces h, h.
The crystals of the Figures 4 and 4a are the two-dimensional counter parts of hemihedric and holohedric three-dimensional crystals. The 2-D Oblique Crystal System has two Classes, 2 and 1, of which 2 is 'holohedric' -- here we should call it totilinear -- and 1 is 'hemihedric' -- here we should it semilinear. As we have seen, crystals of these two Classes can have the same external shape, but will behave in a different way physically or chemically, revealing their difference.
The next Figures show yet other possible aspects that faces can present to the environment, faces belonging to crystals of our present Class, namely 1.
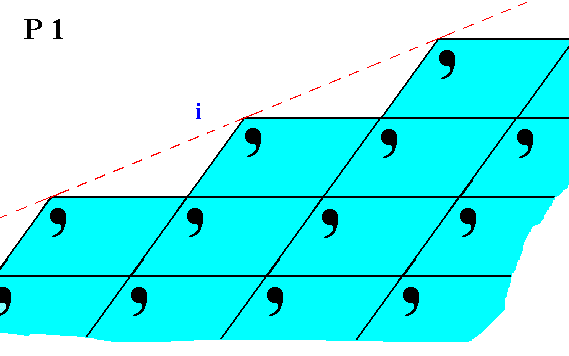
Figure 5. Atomic aspect presented by the face i of a 2-D crystal belonging to Class 1.
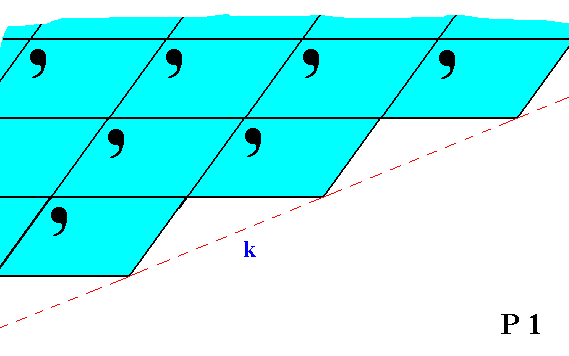
Figure 6. Although the face k is parallel to the face i in Figure 5, they are not equivalent. This non-equivalence is evident from their differing atomic aspects to the environment.
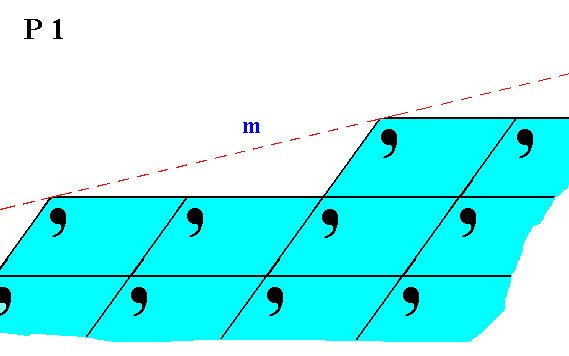
Figure 7. Atomic aspect presented by the face m of a 2-D crystal belonging to Class 1.
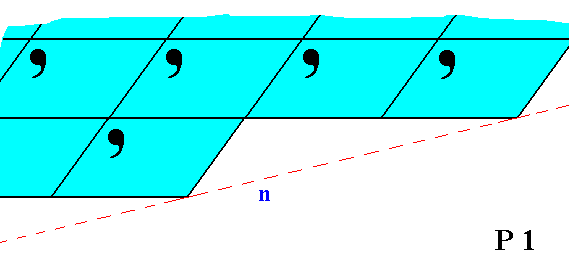
Figure 8. Although the face n is parallel to the face m in Figure 7, they are not equivalent. This non-equivalence is evident from their differing atomic aspects to the environment.
Rectangular Net.
In Figure 9 a possible rectangular (primitive) net is drawn, and the axial directions are indicated.
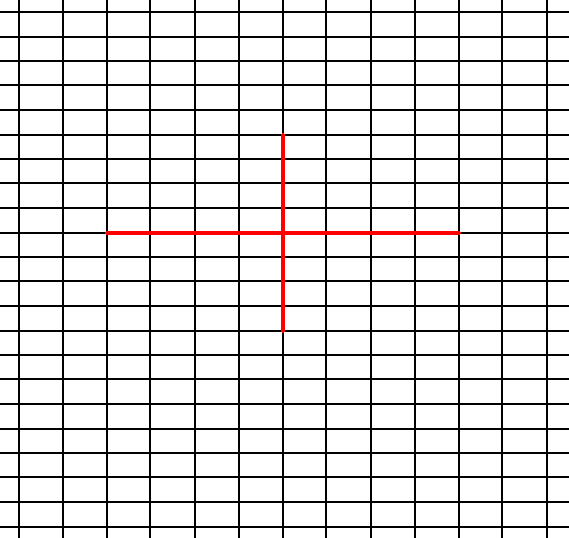
Figure 9. A possible rectangular net ( 2-D lattice). This net can accommodate several types of motifs, such that they are periodically repeated across the 2-D plane, according to the geometry of such a net. The axial directions (i.e. crystallographic axes) are indicated. The two axes are perpendicular to each other, but are not equivalent. The nodes of the net are at the intersections of the lines. These nodes are equivalent points.
In constructing 2-D crystal faces we know that only those faces are possible that can be constructed by the periodic stacking of the building blocks (the meshes of the net).
Let us start with the Point Group (= Crystal Class) m. Crystals belonging to this Class exhibit a point symmetry m, which means that macroscopically the only symmetry element they possess is a mirror line.
When we introduce a face parallel to the longer crystallographic axis, that face will be duplicated in virtue of the action of the mirror line resulting in a Form consisting of two faces that are symmetrical to each other, and in the present case moreover parallel to each other.
See Figure 10.
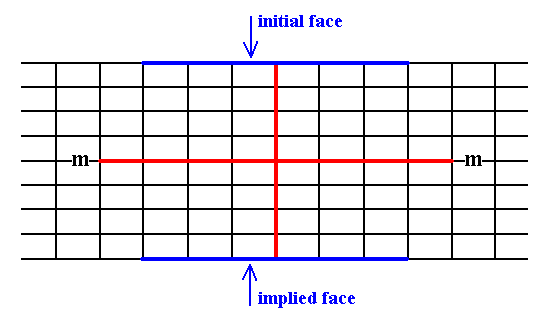
Figure 10. An introduced face parallel to the longer crystallographic axis implies a second face in virtue of a mirror line (m) (In order to make descriptions simple the mirror line (as the only point symmetry element is chosen such that it is aligned with one of the crystallographic axes (This can also be restated as follows : There is only one point symmetry element, namely a mirror line, and we choose the axial system such that one axis coincides with that mirror line).
The resulting face pair is a possible Form of the present Class. It is an open Form.
Another possible Form can be derived from a (possible) face having a different orientation with respect to the crystallographic axes :
Figure 11. An introduced face not parallel to either crystallographic axis implies a second face in virtue of the action of the mirror line (m).
The resulting face pair is a possible Form of the present Class. It is an open Form.
It is imaginable that the location of the system of crystallographic axes was chosen such that the horizontal axis cuts through the horizontal middle lines of the relevant building blocks (instead of coinciding with their horizontal edges). The horizontal axis should then -- like before, in order to let the description of the crystals be simple -- coincide with the horizontal mirror line. See Figure 11a.
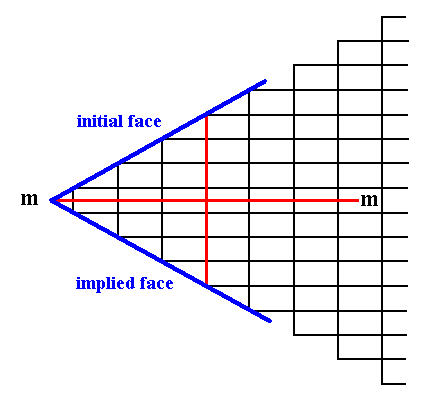
Figure 11a. The same initial and implied faces as in Figure 11.
Because of the chosen location of the axial system the corner formed by the two faces consists of one building block only (instead of two in the case of Figure 11). Although the corners become sharper in this way, and as such more neatly expressed in drawings, we prefer the crystallographic axes to coincide with the edges of the building blocks (unit meshes) instead of somehow going through their interior.
Another possible face parallel to the shorter crystallographic axis does not imply a second face because it is perpendicular to the mirror line, which now maps the face onto itself.
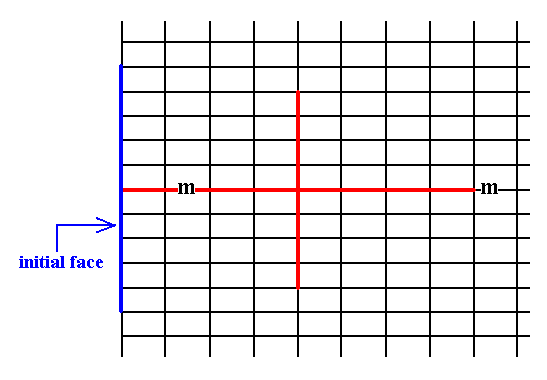
Figure 12. An introduced face perpendicular to the mirror line is mapped onto itself, resulting in a Form consisting of a single face. Also this is an open Form.
Introducing a possible face having yet another orientation with respect to the axial system leads to its reflection by the mirror line, resulting in yet another Form consisting of two faces that are symmetrical to each other. See Figure 13.
Figure 13. An introduced face that is inclined to the mirror line implies a second face, symmetrically related to the initial face. The resulting face pair is a possible (open) Form of the present Class (Recall that the faces as drawn must be imagined to be extended indefinitely, because only their orientations are being considered).
In order to constitute a crystal, the open forms must combine in such a way that a closed face configuration is the result, like the one depicted in the next two Figures.
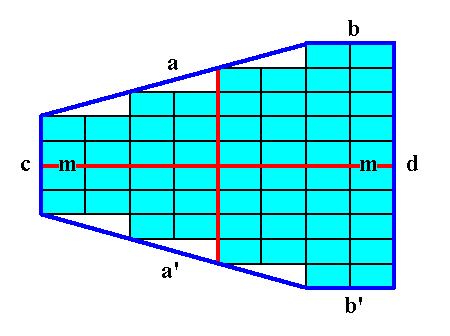
Figure 14. A 2-D crystal is formed from a combination of four individual Forms :
(a + a'), (b + b'), (c), (d).
The final result is shown in the next Figure.
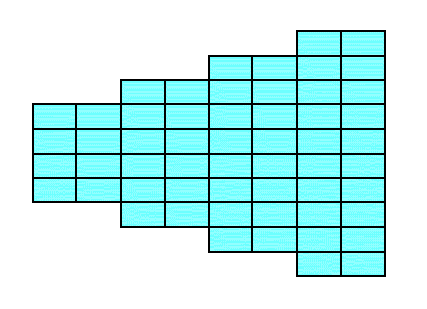
Figure 14a. The 2-D crystal emerging from the construction in Figure 14. It belongs to the Class m of the 2-D Rectangular Crystal System.
The next two Figures give yet another possible combination of Forms, resulting in a crystal.
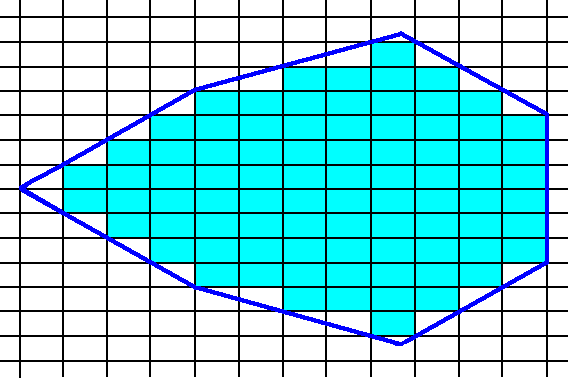
Figure 15. construction of a 2-D crystal by combining several Forms of the Class m.
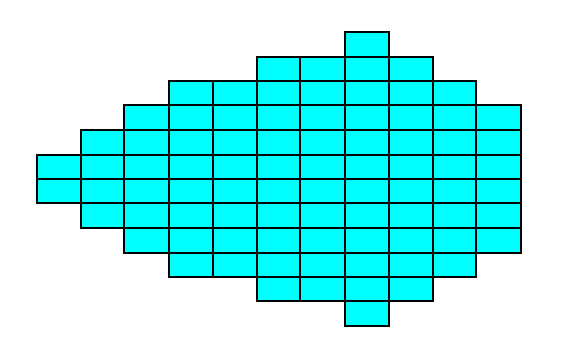
Figure 15a. Result of the construction of Figure 15. A 2-D Crystal of the Class m of the 2-D Rectangular Crystal System.
A combination of three Forms, one consisting of two horizontal faces, one consisting of a vertical face, and one consisting of another vertical face, can yield a crystal having a rectangular shape and strongly elongated in the direction of the shorter dimension of the building block. This is so because a face parallel to the longer side of the unit mesh, and so, in our case, a horizontal face, cuts through a lesser number of nodes than a face parallel to the shorter side of that unit mesh (building block). So when no other factors interfere the crystal will grow fastest in the vertical direction. And because the vertical faces do not taper towards each other but are parallel, the fast growing horizontal faces will not grow themselves out of existence. Consequently the crystal will assume a rectangular shape, markedly elongated in the vertical direction. See Figure 16.
Figure 16. A crystal of the Class m of the 2-D Rectangular Crystal System. It has an elongate habit.
The present Point Group (Crystal Class) m can be the translation-free residue of three Plane Groups, Pm, Pg and Cm depending on the symmetry and distribution of motif units (standing for chemical (sub-)units in the crystal).
We start with giving a motif pattern representing Plane Group Pm.
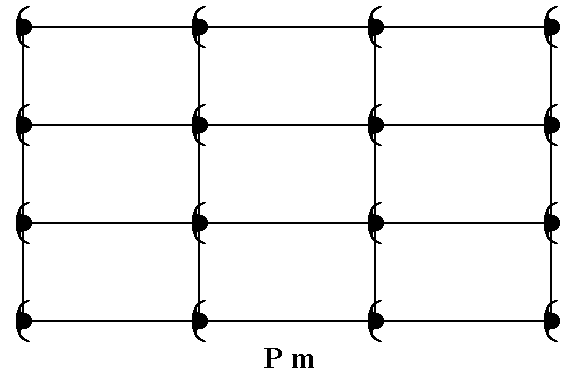
Figure 17. A pattern of periodically repeated motifs representing Plane Group Pm.
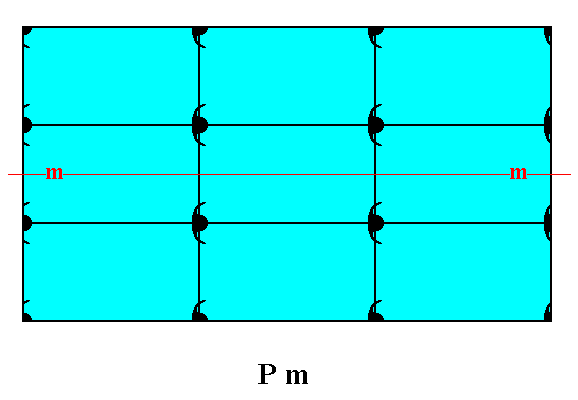
Figure 18. Atomic aspects presented to the growing environment of a 2-D crystal composed of three Forms (one consisting of the top and bottom faces of the crystal, the second consisting of the left face, and a third consisting of the right face of the crystal) of the Class m. The point symmetry m of the crystal is indicated by a mirror line (m). Although the crystal has a rectangular shape, we can -- while inspecting its internal structure, as given in the present Figure -- clearly see that a vertical mirror line is absent (also when all translations would be eliminated), implying the non-equivalence of the two vertical faces, which indeed present different atomic aspects to the environment. When we later discuss the Class 2mm, we'll see that in that Class rectangular crystals can occur having the full point symmetry of a rectangle, a 2-fold rotation axis and a horizontal as well as a vertical mirror line. So the Class 2mm is a 2-D analogue of the holohedric class of a 3-D crystal system, while the Class m is a 2-D analogue of a hemihedric class of a 3-D crystal system. We can call the Class 2mm the totilinear Class, and the Class m a semilinear Class of the 2-D Rectangular Crystal System.
When no other factors interfere, the crystal, depicted in this Figure, would assume an elongated shape in the direction of the shortest side of the building block.
The incomplete motifs at the faces indicate chemical units with unsatisfied or distorted chemical valences.
As was discussed at the Figures 11 and 11a, we prefer to let the crystallographic axes coincide with the edges of the unit meshes (building blocks), which here implies that the mirror line (m) coincides with the horizontal edges of the relevant (and from a microscopic viewpoint all) unit meshes. So Figure 18 should be drawn as follows :
Figure 18a. Atomic aspect of a 2-D crystal composed of three Forms (one consisting of the top and bottom faces of the crystal, the second consisting of the left face, and a third consisting of the right face of the crystal) of the Class m. The point symmetry m of the crystal is indicated by a mirror line (m).
The possible face, depicted -- as initial face -- in Figure 11, presents the following atomic aspect to the growing environment of a 2-D crystal possessing that face :
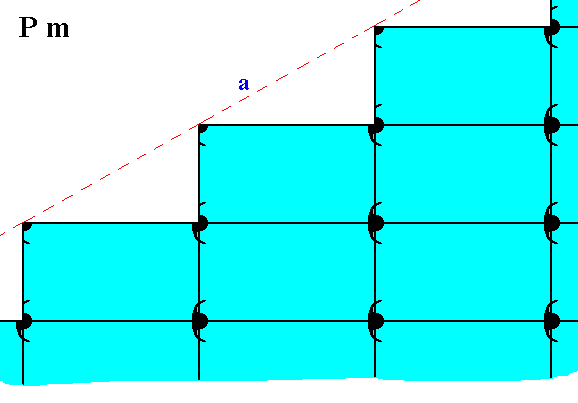
Figure 19. Atomic aspect presented to the environment of the (initial) face (a) depicted in Figure 11.
The possible face, depicted -- as initial face -- in Figure 13, presents the following atomic aspect to the growing environment of a 2-D crystal possessing that face :
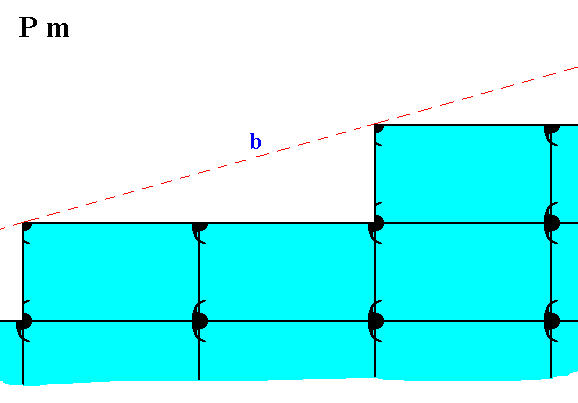
Figure 20. Atomic aspect presented to the environment of the (initial) face (b) depicted in Figure 13.
Sometimes the crystal habit, i.e. its (intrinsic) external shape, can simulate a higher symmetry than it actually has. Let's take the 2-D Crystal of the Class m depicted in the next Figure. Here the point symmetry m is clearly expressed by its external shape :
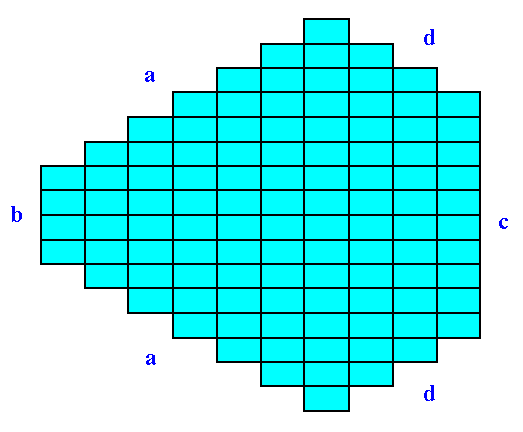
Figure 21. A two-dimensional crystal of the Class m.
The (equivalent) faces a, a grow at a lower rate than the (equivalent) faces d, d, so the a, a faces are more prominent. The development of the faces clearly reveals the crystal's point symmetry, namely m.
Now suppose we have a crystal belonging to the same Class (m) and also to the same Plane Group as the above mentioned crystal, but with a slightly different chemical composition, like for (a 3-D) instance, Sodium Clorate and Sodium Bromate. The point symmetry of the motifs, i.e. of the chemical units, is (expected to be) totally (i.e. in every respect) the same in either case, that's why they belong to the same Plane Group. The chemical difference however causes the d, d faces to grow more slowly as in the former case, indeed they grow precisely as slow as the a, a faces do (by supposition). The effect is that both face types, a, a and d, d, will exhibit the same prominence on the crystal, making the crystal to appear to belong to the Class 2mm, to which in reality it does not belong. See Figure 22.
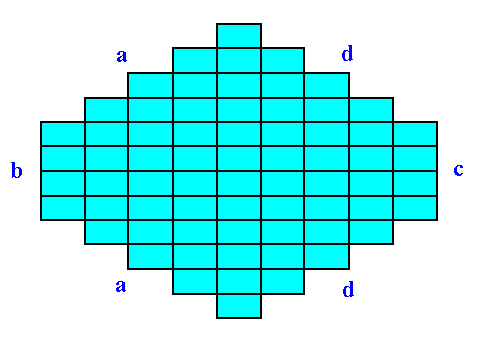
Figure 22. A two-dimensional crystal belonging to the Class m , and to the same Plane Group as the crystal in Figure 21.
Because of a slight chemical difference the crystal simulates a 2mm symmetry.
The next two Figures show -- symbolically -- the mentioned slight chemical difference between the crystal of Figure 21 and that of Figure 22.
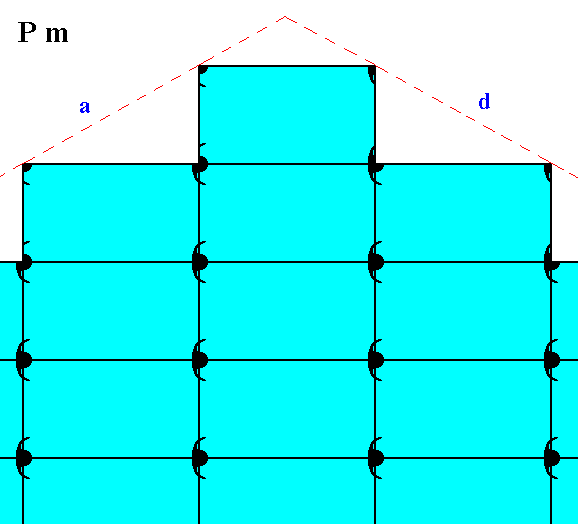
Figure 23. Motifs and atomic aspects of the faces a and d of the crystal of Figure 21.
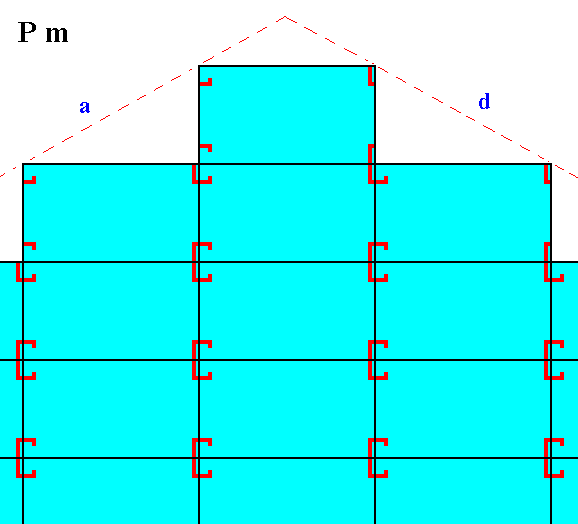
Figure 24. Motifs and atomic aspects of the faces a and d of the crystal of Figure 22.
So the chemical composition and the implied relative growth rates of the different faces strongly determine the intrinsic crystal habit.
In the next Part we will continue our investigation and consider the second Plane Group (Pg) of the 2-D Crystal Class m.
To continue, click HERE for Part Ten.
back to homepage