
back to homepage
The External Shapes of periodic 2-D arrays of repeated two-dimensional motifs
Rectangular Net. (continued)
We continue our investigation concerning the faces, Forms and combinations of Forms in two-dimensional crystals. In the previous Part we had made a beginning with the study of the Crystal Class m of the 2-D Rectangular Crystal System (based on the Rectangular Net). We considered the first Plane Group, Pm belonging to that Class (Point Group).
Now we will consider its second Plane Group, Pg.
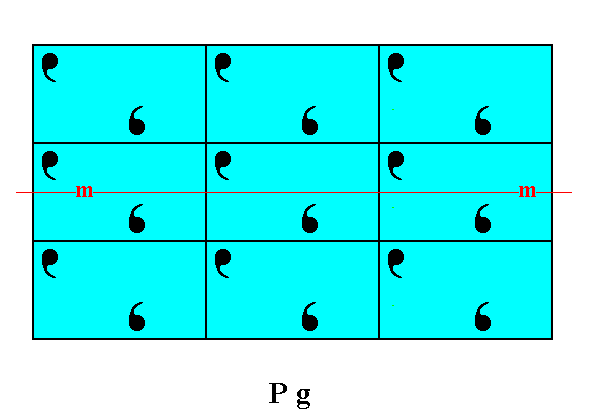
Figure 1. Atomic aspects presented (to the growing environment) by a two-dimensional crystal of the Class m. The point symmetry is indicated by the mirror line (m). Although the crystal has a rectangular shape, it does not possess the full symmetry of a rectangle. For instance, a vertical mirror line is absent, as can be seen when inspecting the internal content, depicted in this Figure. The crystal has the same shape as the one depicted in Figure 18 in Part Nine, and has also the same point symmetry. Their total symmetry content is, however, different : The mirror line, as depicted here in this Figure, will only emerge when all translations are eliminated (i.e. when we consider the crystal from a macroscopic point of view). Not until then it is a glide line. But just because a mirror line does emerge when the crystal is viewed macroscopically, it belongs to the Class m (provided that such a mirror line is the only symmetry element present at the macroscopic level). In the Figure we can clearly see that the atomic aspect presented to the environment is the same for top and bottom faces except for a translational difference -- which is not visible at the macroscopic level -- but is different for the left and right faces. The latter difference will manifest itself in the chemical and / or physical behavior of the respective faces.
The difference between the crystal of Figure 18 of Part Nine and the one depicted here -- as a difference in their total symmetry content -- can be accounted for by their having motifs of a different sort, which fact can be translated in their having a different chemical composition, different in such a way that the total symmetry content is affected as described.
As for the position, as drawn, of the mirror line m, expressing the point symmetry, see the remark introducing Figure 18a in Part Nine and the explanation of that Figure.
Let us give Figure 18 of Part Nine again for easy comparison with the above Figure.
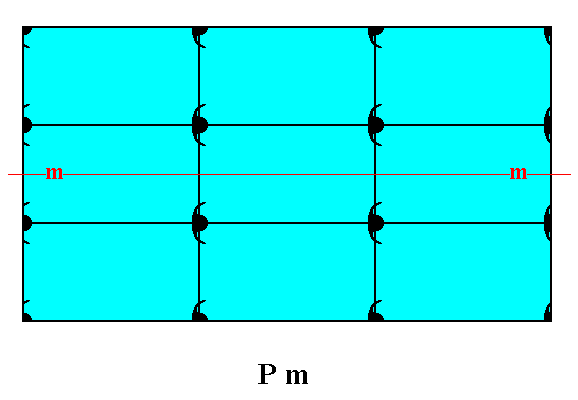
Figure 1a. The mirror line, indicating the point symmetry of the crystal, will still be there when all translational symmetry is taken into account (i.e. when we look to it microscopically and detecting translations), in contrast to the case depicted in Figure 1. The difference between these two rectangular crystals -- which belong to the same Crystal Class, namely m -- a difference in total symmetry content, is, as can be seen from the figures, caused by the presence of different motifs, standing for different chemical units.
In explaining Figure 1 we stated : "In the Figure we can clearly see that the atomic aspect presented to the environment is the same for top and bottom faces except for a translational difference -- which is not visible at the macroscopic level ". The next three Figures show this explicitly with respect to those top and bottom faces. They show that when the glide translation vector becomes zero, then the faces turn out to be symmetrical with respect to the glide line g -- which consequently becomes a mirror line -- and thus to be equivalent (from a macroscopical perspective).
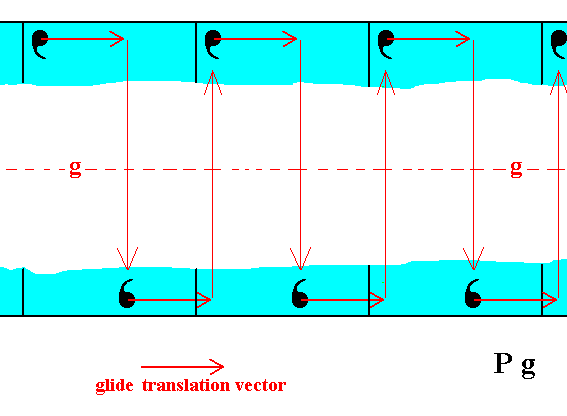
Figure 1b. The motifs of the top and bottom faces of the 2-D crystal of Figure 1 are related by a glide line (g), i.e. related by a translation followed by a reflection, as indicated. So the positions of the motifs associated with the top face are analogous to those of the bottom face except for a horizontal shift (according to the glide translation vector). If we undo this shift then the configuration of the motifs associated with the top face is symmetrical with respect to that of the motifs associated with the bottom face of the crystal. See Figures 1c and 1d.
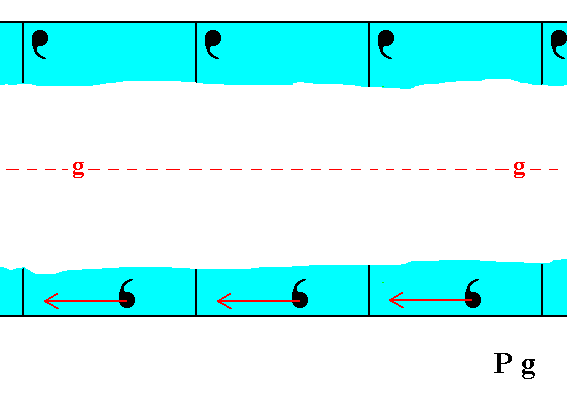
Figure 1c. The horizontal translational difference of the upper and lower motif configurations is eliminated.
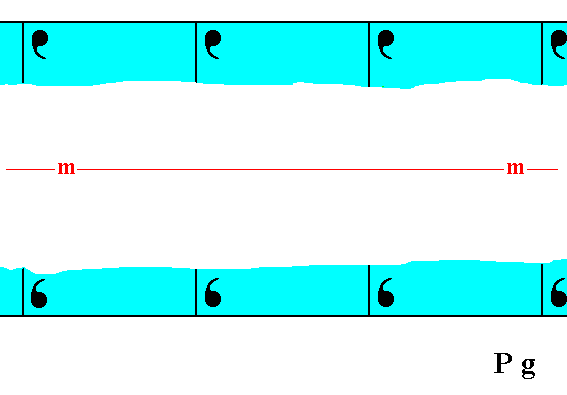
Figure 1d. The top and bottom faces are now symmetrical with respect to the glide line, which consequently becomes a mirror line.
A possible face of a crystal of Class m and Plane Group Pg having a different orientation than the ones above present the following atomic aspect to the environment :
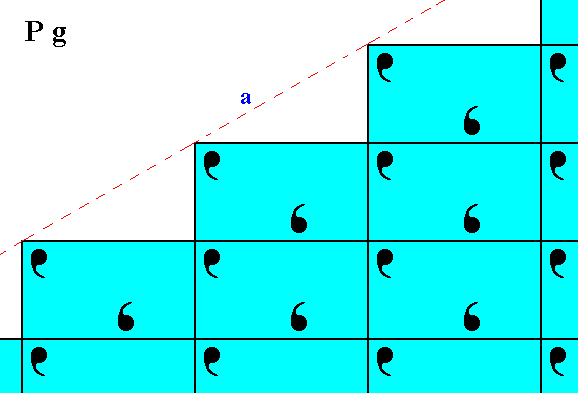
Figure 2. Atomic aspect as represented to the environment by the initial face depicted in Figure 11 of Part Nine.
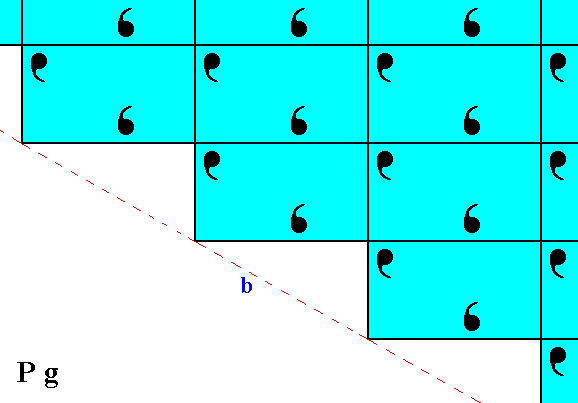
Figure 3. Atomic aspect as presented to the environment by the implied face depicted in Figure 11 of Part Nine. Although the faces a of Figure 2, and b of the present Figure are equivalent, i.e. they can be parts of one and the same Form -- this Form having a point symmetry m -- they seem to present a different atomic aspect to the environment as can be seen from the Figures. But this difference involves only a shift along a straight line : When all glide translations (which are only microscopically visible) are eliminated, i.e. when the crystal is viewed at the macroscopic level, the faces are symmetrical with respect to each other.
In any pattern representing Plane Group Pg there are horizontal glide lines, which means that when the pattern is shifted half a horizontal unit mesh dimension along the glide line followed by a reflection with respect to that line, it is mapped onto itself. And if we remove the translational component from this operation, then only reflection remains : The glide line becomes a mirror line. Expressed in other words : If we change the pattern such that the shift of half a unit mesh dimension is not necessary anymore for having mapped the pattern onto itself, then only a reflection operation is necessary to accomplish that mapping.
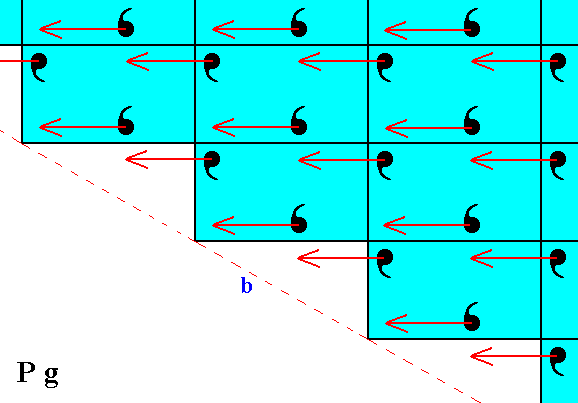
Figure 4. Undoing the horizontal shift (indicated by arrows), i.e. eliminating the translational component of the glide lines.

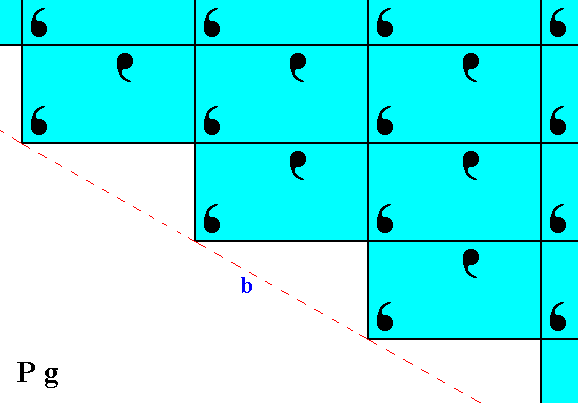
Figure 5. The result of the undoing of the horizontal shift, indicated in Figure 4, is given in the lower half of the present Figure. This then is directly compared with the pattern of Figure 2, which is (again) depicted in the upper half of the present Figure. We can clearly see that the two halves (top and bottom halves) are fully symmetric, meaning that the faces a and b are equivalent.
Another orientation of a possible face effects yet another atomic aspect to the environment. See Figure 6.
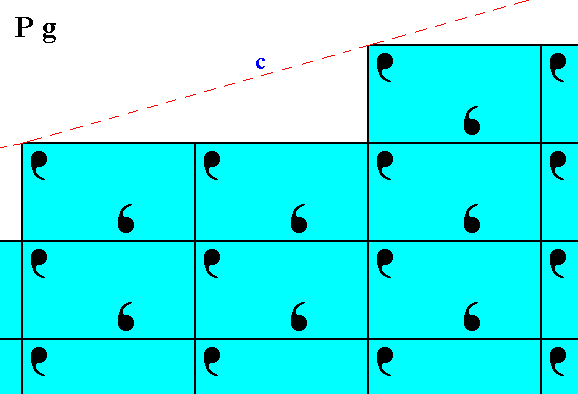
Figure 6. Atomic aspect of the initial face of Figure 13 in Part Nine -- in the present Figure indicated by c.
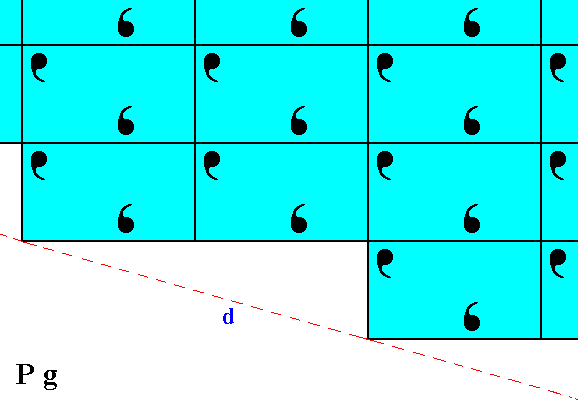
Figure 7. Atomic aspect of the implied face of Figure 13 in Part Nine -- in the present Figure indicated by d. The atomic aspect which this face presents to the environment looks somewhat different from that of the face c of Figure 6. But the difference only consists of a horizontal shift (of a microscopical magnitude) of half the length of the unit mesh, and is macroscopically not visible.
When we shift the pattern of motifs of Figure 7 to the left by half a horizontal unit mesh dimension, i.e. when we eliminate the glide translational difference of this pattern with that of Figure 6, then we -- like in the previous case -- obtain two symmetrical halves, indicating that the faces c and d are equivalent. See Figure 8.

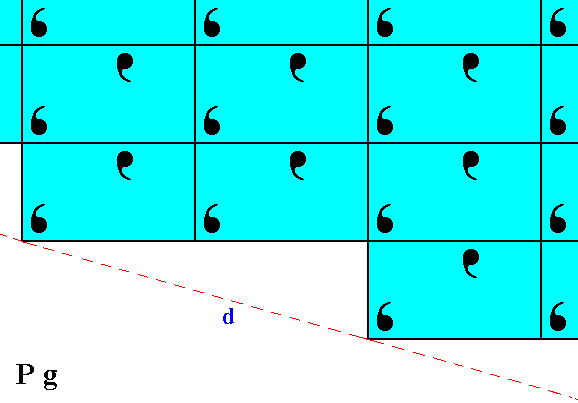
Figure 8. After removing the glide translational difference between the pattern of Figure 6 and that of Figure 7, we can see that they are symmetrically related to each other with respect to a horizontal mirror line, expressing the point symmetry of the present Class m.
Now we will consider the atomic aspects in cases where we have to do with the third (and last) Plane Group belonging to the Point Group m. It is the Plane Group Cm.
To begin with let us again give a pattern (of motifs) representing the Plane Group Cm :
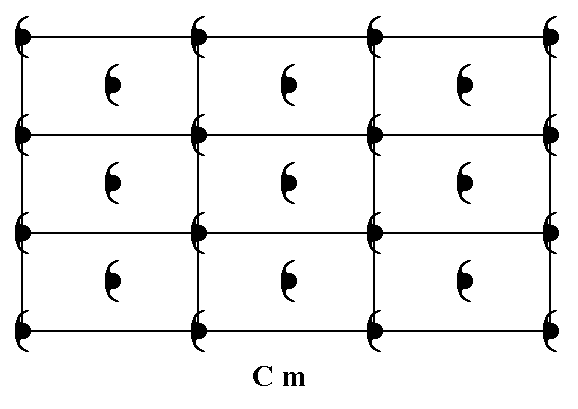
Figure 9. A pattern of periodically repeated motifs, representing Plane Group Cm. The periodicity of the pattern is based on (i.e. described by) a centered rectangular net.
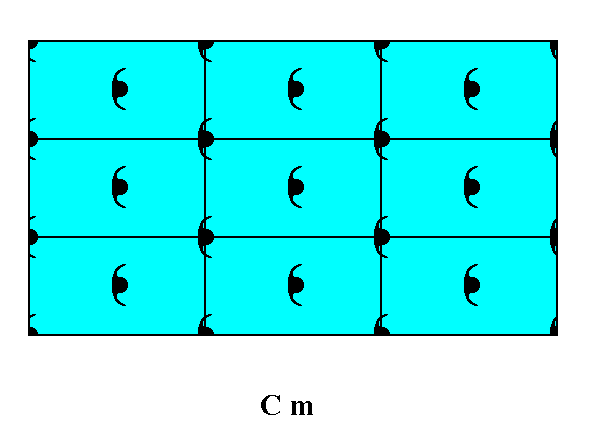
Figure 10. Atomic aspect presented by the faces of a 2-D crystal. The crystal consists of a combination of three Forms : one consisting of the top and bottom faces, a second consisting of the left face, and a third consistinf of the right face of the crystal.
The incomplete motifs at the faces express unsatisfied or distorted chemical valences.
Other possible faces, presenting yet another atomic aspect to the environment, are given in the next Figure.
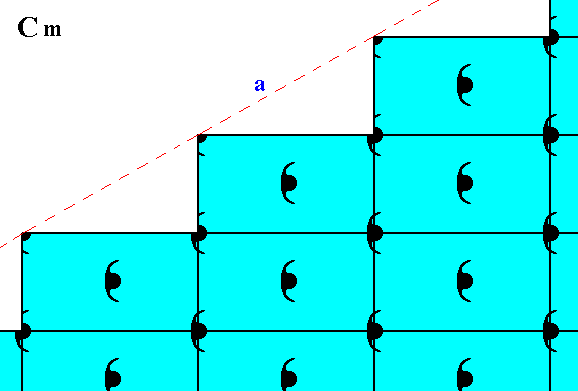
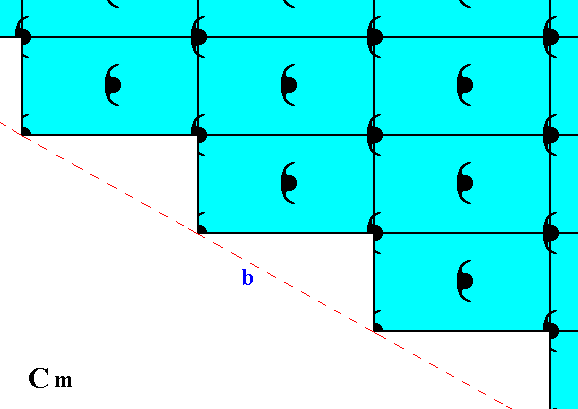
Figure 11. Atomic aspect presented to the environment by the initial and implied faces of Figure 11 in Part Nine. In the present Figure these faces are indicated by a and b. As can be seen, the whole pattern, and consequently also the face pair a, b, is symmetric with respect to a horizontal mirror line, expressing the point symmetry m of the pattern.
Still other possible faces, presenting yet another atomic aspect to the environment, are depicted in Figure 12.
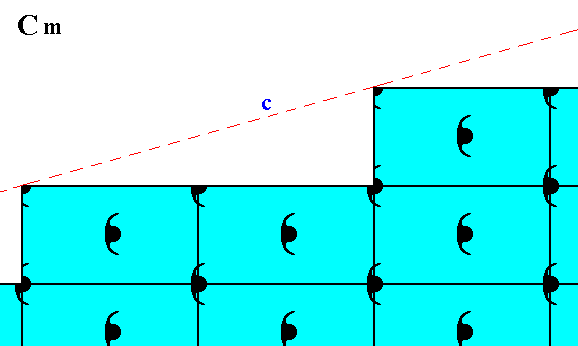
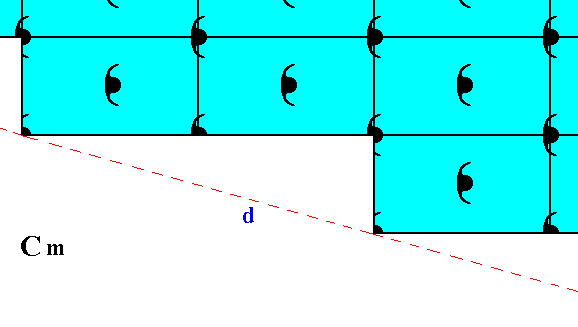
Figure 12. Atomic aspect presented to the environment by the initial and implied faces of Figure 13 in Part Nine. In the present Figure these faces are indicated by c and d. As can be seen, the whole pattern, and consequently also the face pair c, d, is symmetric with respect to a horizontal mirror line, expressing the point symmetry m of the pattern.
We have now exhaustively considered the Class m of the 2-D Rectangular Crystal System. The second and last Class of this System is the Class 2mm, which means that the point symmetry consists of a 2-fold rotation axis and two types of mirror lines.
Figure 13. An introduced face, perpendicular to one of the crystallographic axes, implies a second face, because of either the action of the 2-fold rotation axis or of the mirror line parallel to it. The mirror line perpendicular to the introduced face has no effect on this face. The resulting face pair is a possible Form of the Class 2mm. It is an open Form, and can only exist in (2-D) crystals when it combines with other Forms of the Class such that a closed face configuration is formed.
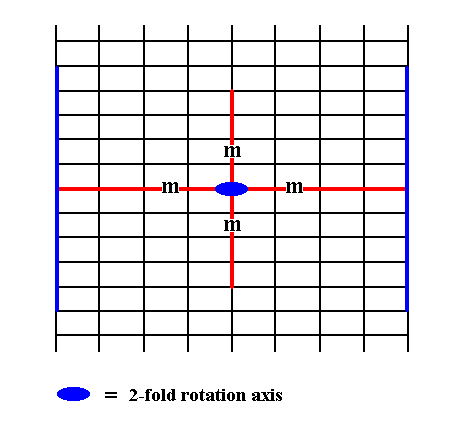
Figure 14. An introduced face, perpendicular to the other of the crystallographic axes, also implies a second face, because of either the action of the 2-fold rotation axis or of the mirror line parallel to it. The mirror line perpendicular to the introduced face has no effect on this face. The resulting face pair is yet another possible Form of the Class 2mm. It is an open Form, and can only exist in (2-D) crystals when it combines with other Forms of the Class such that a closed face configuration is formed.
These two Forms can enter into a combination with each other generating a 2-D crystal of the Class 2mm (Recall that for faces to be possible only their orientation matters) :

Figure 15. A 2-D crystal of the Class 2mm, resulting from a combination of two Forms (depicted in Figures 13 and 14), one consisting of the top and bottom faces, the other of the left and right faces. A crystal of the same shape we already met in the Class m (Figure 16 in Part Nine), but there the crystal was the result of the combination of three Forms : one consisting of the top and bottom faces, the second consisting of the left face, and the third consisting of the right face. Although the two crystals have the same shape they have different symmetries. They are elongated in the direction of the shortest unit mesh dimension because the faces growing in this direction cut through less lattice nodes than the other two faces of the crystal do, effecting them to be fast growing faces. They do not grow themselves out of existence because the other two faces are parallel to each other.
Another Form can be derived from yet another initial face. See Figure 16.
Figure 16. An introduced face is first duplicated by one of the mirror lines, and then the generated face pair is again duplicated by the other mirror plane. The 2-fold rotation axis does not add anything new. The resulting face configuration -- consisting of four faces -- is a closed Form, and can as such represent a 2-D crystal. Its shape is a rhombus. See the next two Figures for the final result.
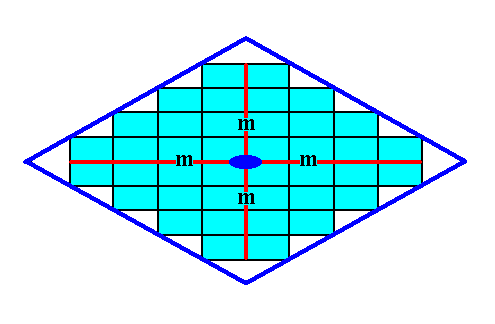
Figure 16a.
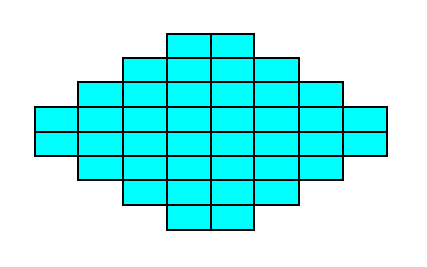
Figure 16b. A two-dimensional crystal of the Class 2mm of the 2-D Rectangular Crystal System. The crystal consists of one Form only.
The Form of which the above crystal consists can still combine with other Forms. In the next Figures we show a combination of this Form with the Form of Figure 14.
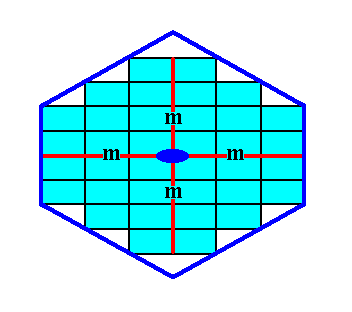
Figure 17.
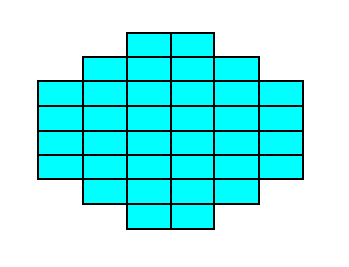
Figure 17a. A two-dimensional crystal consisting of two Forms of the Class 2mm.
Another Form can be generated from an initial face having yet another orientation.
Figure 18. An initial face is multiplied by the symmetry elements, resulting in a single Form having the shape of a rhombus. The final result is shown in the next Figure.
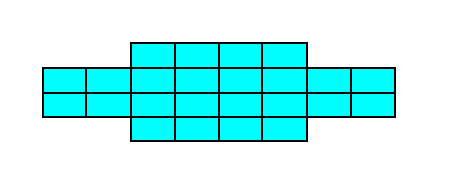
Figure 18a. A two-dimensional crystal of the Class 2mm of the 2-D Rectangular Crystal System. The crystal consists of one Form only.
Again another Form of this Class can be generated from an initial face having yet another orientation. See Figures 19 and 19a.
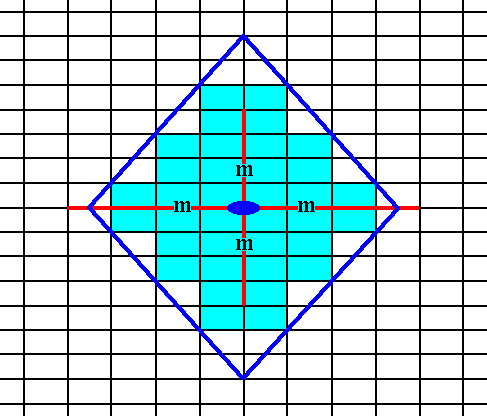
Figure 19. An initial face is multiplied by the symmetry elements, resulting in a single Form having the shape of a rhombus. The final result is shown in the next Figure.
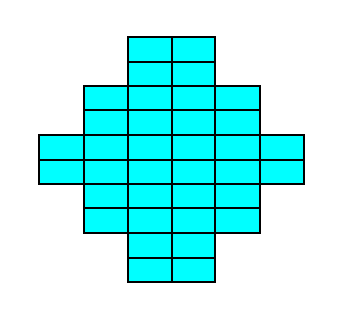
Figure 19a. A two-dimensional crystal of the Class 2mm of the 2-D Rectangular Crystal System. The crystal consists of one Form only.
In the next Part we look to the different Plane Groups that belong to this Crystal Class, in order to visualize the different atomic aspects these faces can present to the growing environment of the 2-D crystals.
To continue, click HERE for Part Eleven.
back to homepage