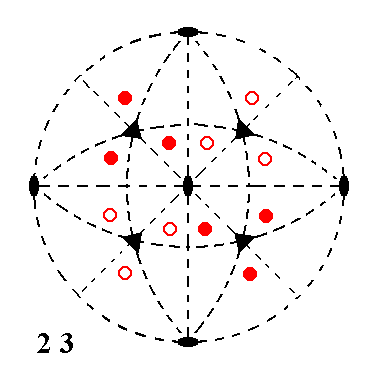
Stereographic projection of the symmetry elements of the Class 23 and of the face poles of its most general Form.
Continuing the investigation of Part Five, we're now going to add a non-diagonal mirror plane to the symmetry content of Class 23. Such a non-diagonal mirror plane is either vertical or horizontal, they are equivalent.
 |
Figure 1. Stereographic projection of the symmetry elements of the Class 23 and of the face poles of its most general Form. |
Next we will add a non-diagonal vertical mirror plane, and we'll see that Class 2/m 3* is generated, a Class which we have already derived earlier :
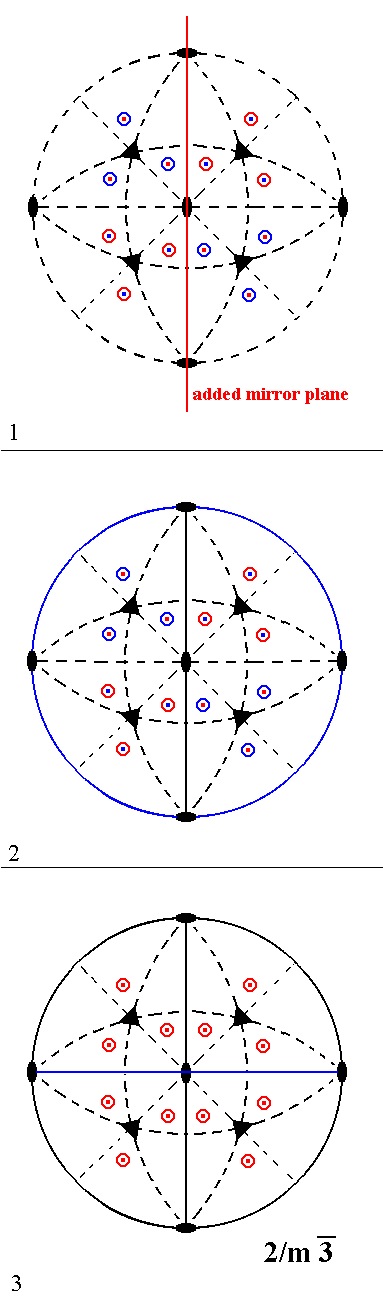 |
Figure 2. Derivation of Class 2/m 3* from Class 2 3 by adding a non-diagonal vertical mirror plane.
(1). Addition of a non-diagonal mirror plane to the symmetry content of Class 23 doubles the number of motifs as indicated.
|
Addition of a vertical non-diagonal mirror plane to the symmetry content of Class 432 yields Class 4/m 3* 2/m. Figure 3 depicts Class 432, and Figure 4 the derivation.
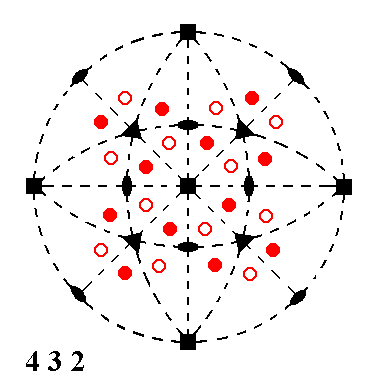 |
Figure 3. Stereographic projection of the symmetry elements of the Class 432 and of the face poles of its most general Form. |
 |
Figure 4. Derivation of Class 4/m 3* 2/m from Class 432 by adding a non-diagonal vertical mirror plane.
(1). Addition of a non-diagonal mirror plane to the symmetry content of Class 432
|
Addition of a non-diagonal mirror plane to Class 2/m 3* is not possible because all the permissible locations for such a mirror plane are already occupied by non-diagonal mirror planes.
Addition of a non-diagonal mirror plane to the Class 4*3m yields Class 4/m 3* 2/m.
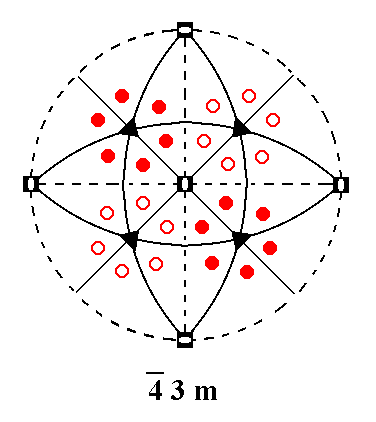 |
Figure 5. Stereographic projection of the symmetry elements of the Class 4* 3m and of the face poles of its most general Form. |
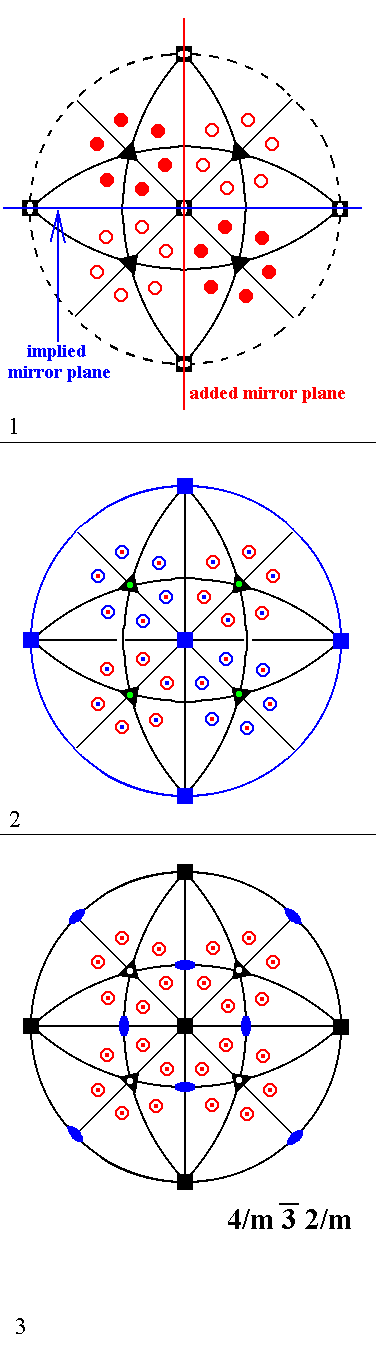 |
Figure 6. Derivation of Class 4/m 3* 2/m from Class 4* 3m by adding a non-diagonal vertical mirror plane.
(1). Addition of a non-diagonal mirror plane to the symmetry content of Class
(3). The diagonal vertical mirror planes, being perpendicular to the horizontal mirror plane, generate two horizontal 2-fold rotation axes (small solid blue ellipses at the perimeter of the projection plane). The 3-fold roto-inversion axes multiply these 2-fold axes, resulting in four inclined 2-fold rotation axes (small solid blue ellipses in the central region of the stereogram). |
Addition of a non-diagonal mirror plane to Class 4/m 3* 2/m is not possible because all the permissible locations for such mirror planes are already occupied with non-diagonal mirror planes.
Still left to investigate is : the addition of a center of symmetry to the symmetry content of Class 4*3m, the addition of a horizontal diagonal 2-fold rotation axis (Horizontal diagonal 2-fold axes are equivalent to the inclined 2-fold axes) to that of the same Class, and the addition of a non-diagonal 2-fold rotation axis, also to (the symmetry content of) that Class. The latter does not to be considered because that Class has already 4-fold roto-inversion axes at the corresponding locations (Recall that a 4-fold roto-inversion axis (as well as a 4-fold rotation axis) is at the same time also a 2-fold rotation axis).
Addition of a center of symmetry to the symmetry content of Class 4* 3m yields
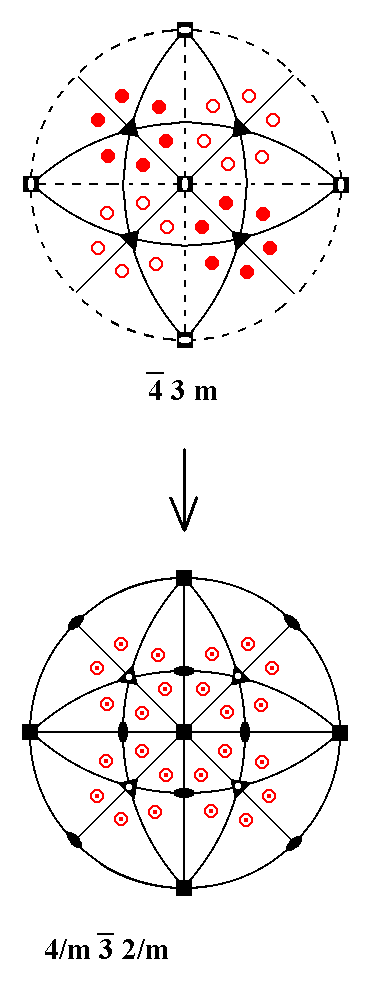 |
Figure 7.
Addition of a center of symmetry to the symmetry elements of the Class 4* 3m doubles the number of motifs. The symmetry of the resulting motif pattern then demands (a) the 4-fold roto-inversion axes to become 4-fold rotation axes (See Remark below), and (b) the presence of three non-diagonal mirror planes (Two vertical and one horizontal). Further we have the coming into being of 2-fold rotation axes -- where none were there -- where there is an intersection of two mirror planes perpendicular to each other (At some of these places there is already a 4-fold axis, and such an axis already implies 2-fold symmetry). (The situation of a vertical mirror plane perpendicular to a diagonally inclined mirror plane is depicted in Figure 7a). Because of the presence of a center of symmetry the 3-fold axes become 3-fold roto-inversion axes (open triangles). |
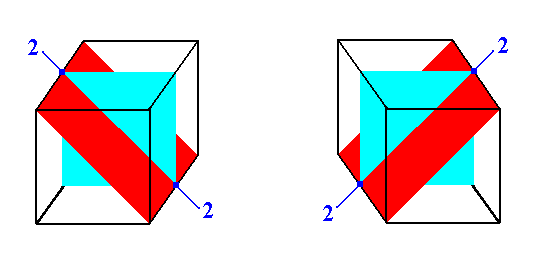
Figure 7a. A vertical mirror plane perpendicular to a diagonally inclined mirror plane.
Remark : In Figure 7 we stated the following "The symmetry of the resulting motif pattern then demands (a) the 4-fold roto-inversion axes to become 4-fold rotation axes."
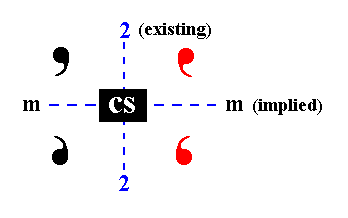
Figure 7b. The presence of a 2-fold rotation axis and a center of symmetry implies a mirror plane perpendicular to that 2-fold axis.
As can be seen from Figure 7b a horizontal mirror plane is implied perpendicular to the 4-fold roto-inversion axis (Recall that such an axis is at the same time also a 2-fold rotation axis), and by the same reason two vertical non-diagonal mirror planes are implied. This means that all permissible mirror planes are now present. This in turn means that the motif pattern -- originated by the doubling of the existing motifs in virtue of the addition of a center of symmetry -- is wholly regular. We now can be sure that, say, the upper left motif cluster in the stereogram will be repeated exactly with every rotation of 900 about the vertical axis, so this axis must now be a 4-fold rotation axis.
The other two 4-fold roto-inversion axes also must become 4-fold rotation axes, because 4-fold roto-inversion axes as such do not admid of the presence of a center of symmetry and because the non-diagonal rotation axes are equivalent to the vertical axis.
(End of Remark)
Addition of a horizontal diagonal 2-fold rotation axis to the symmetry content of Class 4* 3m yields Class 4/m 3* 2/m. See Figure 8.
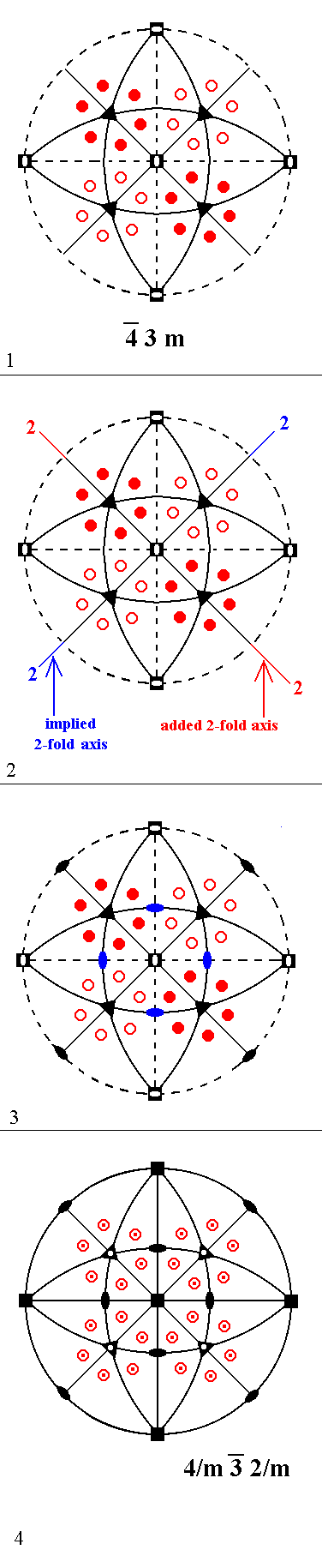 |
Figure 8. Derivation of Class 4/m 3* 2/m from Class 4* 3m by adding a horizontal diagonal 2-fold axis.
(1). Stereogram of the symmetry elements of the Class 4* 3m and of the face poles of its most general Form.
|
Summarizing : Concerning the symmetry combinations having more than one more-than-2-fold axis we have found the following Classes :
In order to know for sure that we have indeed exhaustively derived all possible crystal classes (i.e. symmetry combinations permissible in crystals) that have more than one more-than-2-fold axis, we will summarize schematically what we have done.
Two Classes were given from the outset, namely the basic axial combinations 1 and 2 (Representing the Classes 23 and 432 respectively).
Three more Classes were eventually derived : 2/m 3*, 4*3m and 4/m 3* 2/m.
For convenience we will assign numerals to these five Classes :
This concludes our DERIVATION of the thirty-two Crystal Classes (Done in Parts I, II, III, IV, V and VI). They represent all possible combinations of point symmetric operations that can occur in crystals. A "point symmetric operation" is an operation performed on a figure (like reflection, rotation etc.) that leaves at least one point of that figure unchanged, i.e. such a point is not moved by such an operation. These symmetries and their combinations are therefore called point symmetries. Each combination (including single operations) is (also) called a point group (so there are 32 possible point groups for crystals) because they can be described by the mathematical theory of groups.
In the next series of Essays these Crystal Classes, ordered in six Crystal Systems, are studied one by one. For each Class all the possible Forms will be derived. A Form is a set of equivalent crystal faces, consistent with the symmetry of the Class to which that Form belongs. Real crystals consist either of a single Form or of a combination of Forms belonging to the same crystal class.