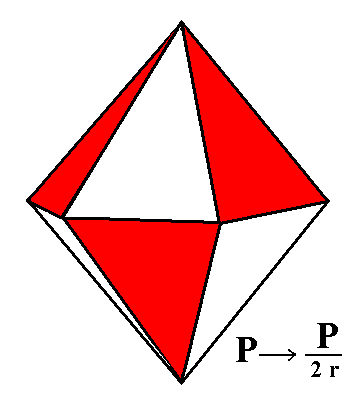
Protopyramid (= hexagonal type I bipyramid)
Deuteropyramid (= hexagonal type II bipyramid)
Dihexagonal Bipyramid
Protoprism (= hexagonal type I prism)
Deuteroprism (= hexagonal type II prism)
Dihexagonal Prism
Basic Pinacoid
From the holohedric protopyramid we will obtain two rhombohedrons when we apply the rhombohedric hemihedric to it, which means that we drop the main (i.e. horizontal) mirror plane and the three vertical mirror planes going through the three crystallographic axes.
In Figure 1 we express this symmetry reduction, applied to the holohedric hexagonal protopyramid, by the alternate suppression and extension of its faces. This process of alternate suppression and extension is carried out on the upper part of the pyramid as well as on the lower part of it, but in such a way that the two processes are not symmetrical to each other but are 600 rotated with respect to each other. This fact expresses the absence of the horizontal mirror plane in the Form to be derived (the rhombohedron).
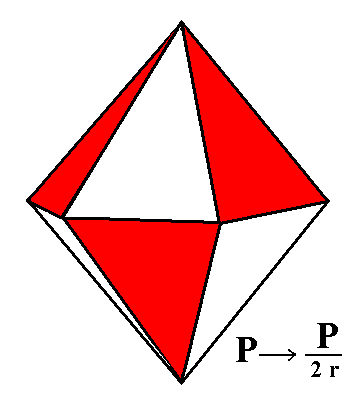 |
Figure 1. From the holohedric Protopyramid is derived one or another Rhombohedron depending which faces will be suppressed. |
One of the rhombohedrons will emerge when we suppress the white faces and allow the red faces to extend. Another rhombohedron will be obtained when we suppress the red faces and allow the white faces to extend till they meet. This latter rhombohedron is depicted in Figure 1a.
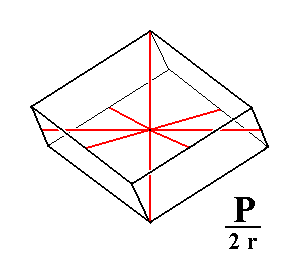 |
Figure 1a. From the white faces of the holohedric Protopyramid is derived a Rhombohedron. The four crystallographic axes are drawn as red lines. The sign "r" in the expression "2r" of the Naumann symbol indicates that we have to do with the rhombohedric hemihedric. |
The rhombohedron is bounded by six rhombi, so all lengths (of sides) are equal. It has six equal polar edges (going from the apex to the equatorial zig-zag edge). The just mentioned equatorial zig-zag edge consists of six equal lines connected with each other in an up and down fashion. Further the rhombohedron has two polar (i.e. apical) corners in each of which three equal polar edges come together. It has six middle corners in each one of which three (2+1) edges come together. The main crystallographic axis goes through the polar corners, i.e. from apex to apex. The horizontal crystallographic axes go through the midpoints of the middle edges. The angular value of the polar edges is the supplement of that of the middle edges
[ The supplement of an angle A is equal to 1800 minus A ].
In order to understand the derivation of the rhombohedron from the holohedric protopyramid we should note that the equatorial plane of the protopyramid is a regular hexagon. When we alternately suppress sides and allow to extend the surviving sides we obtain an equilateral triangle (equilateral trigon), as Figure 1b shows. In this Figure the horizontal crystallographic axes are indicated by red diagonal lines.
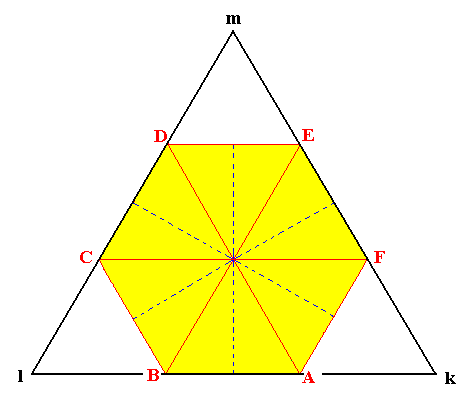 |
Figure 1b. From the regular Hexagon ABCDEF we can derive the equilateral Triangle (regular Trigon) klm, by alternately suppressing sides of the Hexagon and allow the surviving sides to extend till they meet. |
Any horizontal section through the protopyramid (except through one or the other apex) is a regular hexagon. So we can draw one hexagon and interpret it as two superimposed sections of the pyramid, one from somewhere above the equatorial plane and the other from below that plane at an equal distance from it. Let the sides of the hexagons represent the faces of the pyramid.
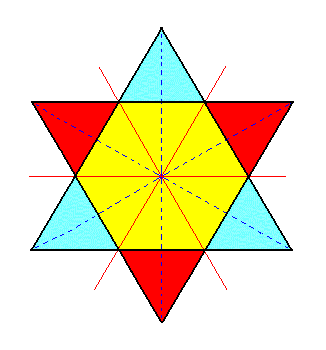 |
Figure 1c. From two identical superimposed regular Hexagons we can derive two equilateral Triangles (regular Trigona) by alternately suppressing sides of one Hexagon (interpreted as the upper horizontal section through the protopyramid) and allow the surviving sides to extend till they meet, and then do the same with the other hexagon but with the whole process 600 rotated with respect to the first. |
The two generated triangles can be interpreted as the upper and lower horizontal sections through the rhombohedron. The sides of these triangles (six in total) can now represent the six faces of the rhombohedron. The lines connecting the apices of the triangles -- namely connecting the apex of a lower ('southern') triangle with that of an upper ('northern') triangle, and the latter again with that of a next lower triangle, etc. -- are the six equal zig-zag going middle edges of the rhombohedron (if we now interpret the upper and lower sections through the rhombohedron at the appropriate distance from the plane of the horizontal crystallographic axes). See Figure 1d.
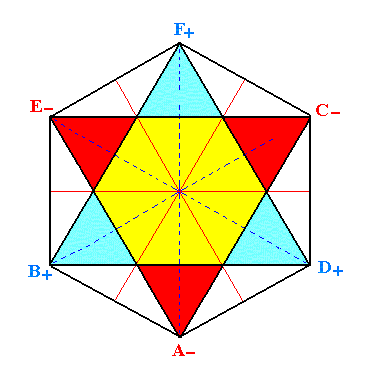 |
Figure 1d. The two superimposed equal Triangles, differing in orientation by a rotation of 600 can represent the Rhombohedron generated (derived) from the Hexagonal Protopyramid. The six lines [A- D+], [D+ C-], [C- F+], [F+ E-], [E- B+] and [B+ A-] are the six zig-zag going middle edges of the Rhombohedron (See also Figure 1e), where "+" means a position above the equatorial plane (i.e. the plane in which lie the horizontal crystallographic axes), and "-" a position below that plane. |
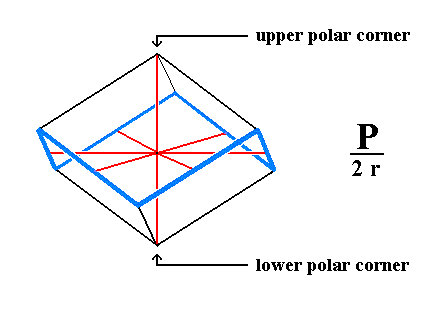 |
Figure 1e. The Rhombohedron of Figure 1a. Its zig-zag middle edges are shown in bold blue. The remaining edges are the polar edges. |
From the holohedric deuteropyramid we can derive the rhombohedric hemihedric Type II hexagonal bipyramid when we subject it to the rhombohedric hemihedric. It does not change its shape, but its symmetry is lowered accordingly. See Figure 2.
 |
Figure 2. The holohedric Deuteropyramid retains its external shape when subjected to rhombohedric hemihedric. |
When we apply the rhombohedric hemihedric to the holohedric dihexagonal bipyramid we will obtain a ditrigonal scalenohedron.
To understand how this Form is derived let us first consider the dihexagonal bipyramid. Any horizontal section (except through its apices) taken from this pyramid is a dihexagon. So also the equatorial plane is a dihexagon. If we apply rhombohedric hemihedric to this plane, then we must drop the three vertical mirror planes (in the plane these are mirror lines) going through the horizontal crystallographic axes (red on the Figure). We have expressed this by the coloring of the sides of the dihexagon (representing faces of the dihexagonal bipyramid) in Figure 3.
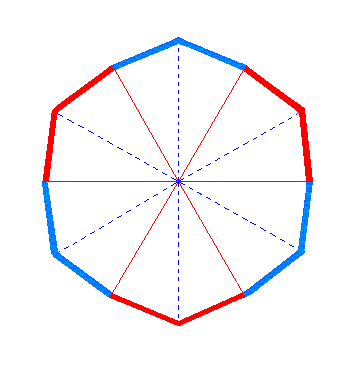 |
Figure 3. The equatorial section of the Dihexagonal Bipyramid. Indicated by coloring is the suppression of the the mirror planes going through the horizontal crystallographic axes (and containing the vertical axis). These axes are indicated by red lines. |
Applying rhombohedric hemihedric means that we must suppress alternate face pairs and allow the remaining face pairs to extend. But the fact that in rhombohedric hemihedric also the equatorial mirror plane must be suppressed demands that there must be no symmetry between the just mentioned process of suppressing alternate face pairs and allowing the others to extend carried out with respect to the upper faces of the bipyramid and that process with respect to the lower faces of that bipyramid. The upper process should be different from the lower one, which (difference) can be achieved by an appropriate rotational difference between the two suppression-extension series. See Figure 3a.
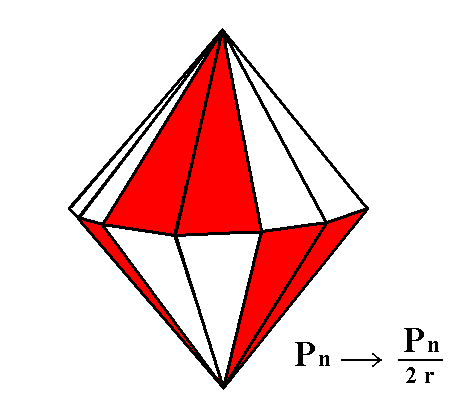 |
Figure 3a. Indication of the alternate suppression of faces of the Dihexagonal Bipyramid. Two Ditrigonal Scalenohedrons can be derived, by either the red faces or the white faces (represented in blue in Figure 3). |
If we extend the red sides (representing faces) at the expence of the blue ones then we get a ditrigonal outline. See Figure 3b.
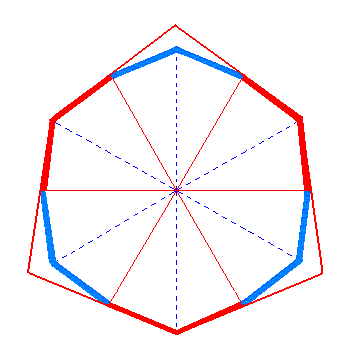 |
Figure 3b. Extending the red sides (representing faces) and suppressing the blue sides (representing faces) results in a ditrigonal outline, again depicted in Figure 3c. The horizontal crystallographic axes are indicated by red lines. |
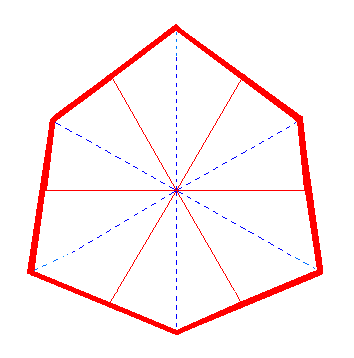 |
Figure 3c. Ditrigon, generated by the extension of the red sides (representing faces) of the Dihexagon of Figure 3. |
In the same way the blue sides (representing faces) can extend at the expence of the red ones, resulting again in a Ditrigon. See Figure 3d.
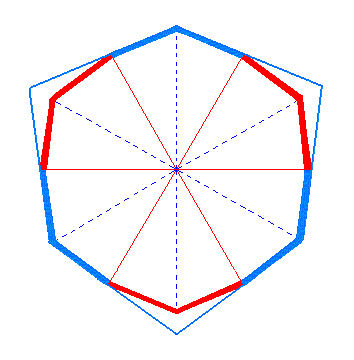 |
Figure 3d. Extending the blue sides at the expence of the red sides yields a Ditrigon. See Figure 3e. |
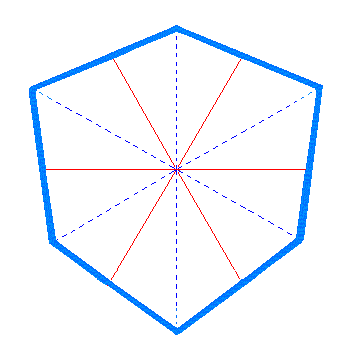 |
Figure 3e. Ditrigon, generated by the extension of the blue sides (representing faces) of the Dihexagon of Figure 3. |
When we superimpose both extension-suppression procedures we get the following (See Figure 3f) :
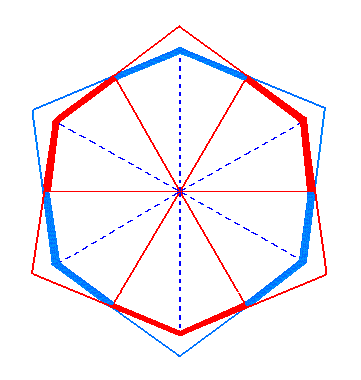 |
Figure 3f. Superposition of the two Ditrigons generated respectively from the red sides and the blue sides of the Dihexagon of Figure 3. |
The two ditrigons are equal but differ in orientation by a rotation of 600. We're now going to interpret them as two horizontal sections through the ditrigonal scalenohedron, one somewhere above the plane of the horizontal crystallographic axes, and the other the same distance below that plane. So the ditrigonal scalenohedron consist of two opposing ditrigonal pyramids that are 600 rotated with respect to each other. This implies that their lines of intersection (separating the two pyramids) assume a zig-zag course. They do not lie in the same plane. The next Figure explains this.
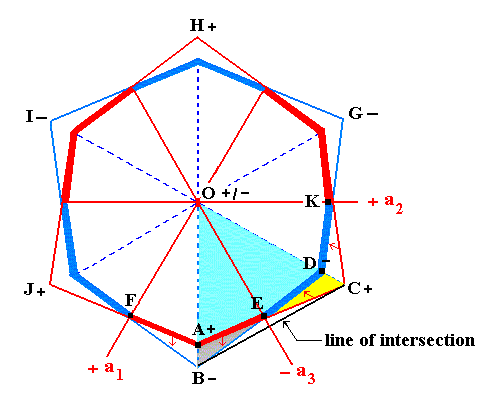
Figure 3g. Derivation of the faces (examplified by two of them) of the Ditrigonal Scalenohedron from the faces of the holohedric Dihexagonal Bipyramid.
The sign "+" relates to positions above the plane of the horizontal crystallographic axes, the sign "-" relates to positions below that plane.
In Figure 3g the bold strong outline consisting of red pairs and blue pairs of sides ( of a Dihexagon) represents the upper as well as the lower faces of a dihexagonal bipyramid. In fact we should imagine that the dihexagon here depicted consists of two identical (also qua orientation) dihexagons. One originates from a section taken somewhere above the equatorial plane of the dihexagonal bipyramid, the other from a section taken a same distance below the equatorial plane. Because they are identical in size and orientation they coincide in the drawing. We must further imagine that these dihexagons represent respectively the upper and the lower faces of the dihexagonal bipyramid.
Now we subject the upper dihexagon to a suppression of the mirror lines parallel to the three horizontal crystallographic axes, a1, a2 and a3 (thin red lines in the above Figure), (that suppression of mirror lines) being expressed by the alternate extension and suppression of side-pairs (representing face pairs) : The red sides are allowed to extend at the expence of the blue sides which are suppressed. In this way a ditrigon is generated, like in Figure 3c.
With the lower dihexagon we do the same, but in such a way that the whole operation differs from the former in its orientation by 600. This means that now the blue sides (representing faces) are allowed to extend at the expence of the red ones which are suppressed. This orientational difference garantees the absence of the equatorial mirror plane in the ditrigonal scalenohedron to be constructed (i.e. to be derived). In this way a ditrigon is generated, like in Figure 3e. The superposition of these two ditrigons was already shown in Figure 3f. In the above Figure (3g) we see this same superposition.
Now we're going to think in terms of faces.
In Figure 3g we can see the following ( "+" refers to positions above, "-" to positions below the equatorial plane, so O+ refers to the upper apex of the bipyramid and of the scalenohedron to be derived, while O- refers to the lower apex) :
[A+ O+ E] is a member of the upper face pair [F O+ A+][A+ O+ E]. It is allowed to extend at the expence of the adjacent face pairs, resulting in [A+ O+ C+].
[D- O- E] is a member of the lower face pair [K O- D-][D- O- E]. It is allowed to extend at the expence of the adjacent face pairs, resulting in [D- O- B-].
The two faces (of the scalenohedron to be generated) [A+ O+ C+] and [D- O- B-] seem to overlap, which of course is not possible. So the one must lie below the other ( [D- O- B-] lies below [A+ O+ C+] ), and their line of intersection is the line [B- C+], see Figure 3g. This line cannot be horizontal (because it starts at B- and ends with C+), but must be inclined. Half of it is below the equatorial plane (the plane of the horizontal crystallographic axes), the other half lies above that plane.
In fact we've now constructed two faces of the scalenohedron one lying below the other, separated by a non-horizontal line of intersection.
If we repeat this construction of faces (of the scalenohedron) six times around the figure formed by the two superimposed ditrigons then we will obtain all the faces of the scalenohedron. This scalenohedron consists of twelve unequilateral triangles. It has six longer and more obtuse edges, for example [B- O+] and [C+ O-] and six shorter and sharper edges, for example [C+ O+] and [B- O-]. These are as followed organized : Directly beneath each longer more obtuse edge lies a shorter sharper edge. For example directly beneath the longer and more obtuse [B- O+] lies the shorter and sharper [B- O-].
In Figure 3g we see that the line [B- C+] goes from the lower ditrigon (blue) to the upper ditrigon (red), and that's of course the reason why the line [B- C+] is not horizontal. It is one of the six equal middle edges of the scalenohedron. The other middle edges are [C+ G-], [G- H+], [H+ I-], [I- J+] and [J+ B-]. As can be seen from their going from the upper ditrigon to the lower and then to the upper again, it is clear that these six middle edges of the scalenohedron go in a zig-zag way.
In Figure 3h we've drawn the ditrigonal scalenohedron, and its orientation with respect to the four crystallographic axes. Figure 3i depicts the same scalenohedron but this time with letters inserted corresponding to those of Figure 3g.
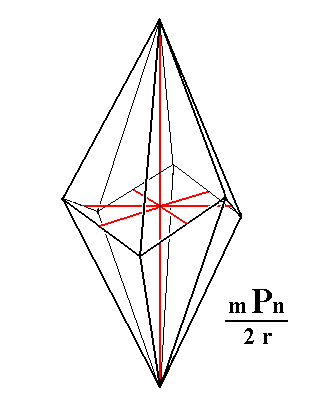 |
Figure 3h. The Ditrigonal Scalenohedron. The four crystallographic axes are drawn in red. |
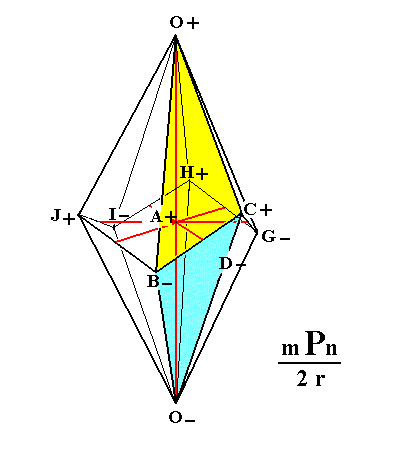 |
Figure 3i. The Ditrigonal Scalenohedron, with letters inserted corresponding to those of Figure 3g. The two faces treated of in Figure 3g are colored. The four crystallographic axes are drawn in red. |
When we apply rhombohedric hemihedric to the holohedric protoprism we obtain a rhombohedric hemihedric type I hexagonal prism. See Figure 4.
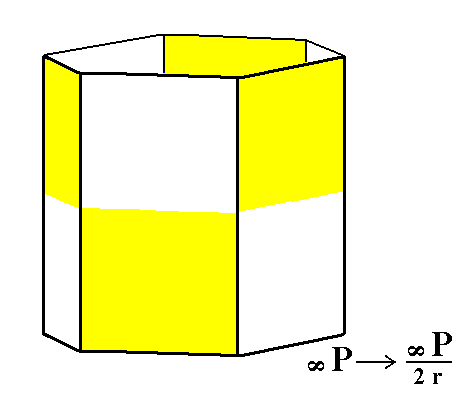 |
Figure 4. The holohedric Protoprism does not alter its shape when subjected to rhombohedric hemihedric, but loses some symmetry. |
From the holohedric deuteroprism we can derive the rhombohedric hemihedric type II hexagonal prism when we subject it to rhombohedric hemihedric. It does not alter its shape but loses some symmetry accordingly. See figure 5.
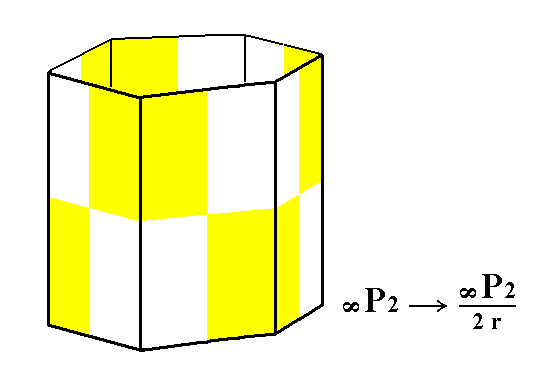
Figure 5. The holohedric Deuteroprism does not alter its shape when subjected to rhombohedric hemihedric, but loses some symmetry.
From the holohedric dihexagonal prism can be derived the rhombohedric hemihedric dihexagonal prism, when we apply rhombohedric hemihedric to it. The prism does not change its shape but is lowered in symmetry. See Figure 6.
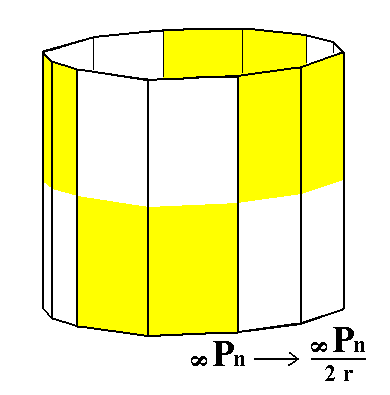 |
Figure 6. The holohedric Dihexagonal Prism does not alter its shape when subjected to rhombohedric hemihedric, but loses some symmetry. |
From the holohedric basic pinacoid we can derive the rhombohedric hemihedric basic pinacoid by subjecting it to rhombohedric hemihedric. Also this Form does not alter its shape but loses some symmetry accordingly. See Figure 7.
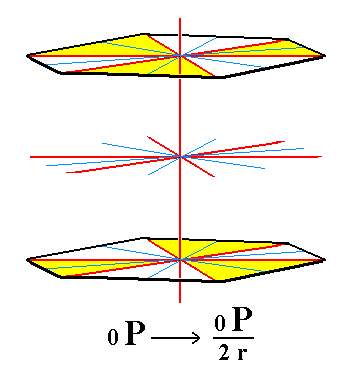 |
Figure 7. The holohedric Basic Pinacoid does not alter its shape when subjected to rhombohedric hemihedric, but loses some symmetry. |
This concludes the derivation of all the Forms of the Ditrigonal-scalenohedric Crystal Class. All these Forms can engage in combinations in real crystals.
FACIAL APPROACH
We will now derive those same Forms by subjecting the basic faces (compatible with the Hexagonal Crystal System) one by one to the symmetry operations of the present Class (the Ditrigonal-scalenohedric Crystal Class).
In Part One we found the following seven basic faces compatible with the Hexagonal Crystal System :
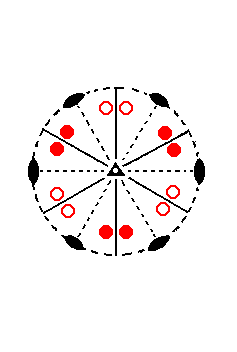 |
Figure 8. Stereogram of the symmetry elements of the Ditrigonal-scalenohedric Crystal Class, and of all the faces of the most general Form. The periphery of the stereogram (i.e. the circle bordering the plane of projection) is dashed, meaning that there is no equatorial mirror plane. The same is the case with respect to those vertical mirror planes that coincide with the directions of the horizontal crystallographic axes. The 2-fold rotation axes (symbolized by small solid ellipses) do not lie in any mirror plane, but are perpendicular to them, i.e. each 2-fold axis is perpendicular to a mirror plane. These mirror planes bisect the angles between the horizontal crystallographic axes. Coinciding with the vertical crystallographic axis (the c axis) is a 3-fold roto-inversion axis, indicated by a solid triangle with a white point in the middle. This axis is equivalent to a 3-fold rotation axis + center of symmetry. |
The face a : ~a : -a : c will give rise to a rhombohedric hemihedric rhombohedron (Figure 1a), when subjected to the symmetry elements of the present Class. To subject a face to the 3-fold roto-inversion axis (in order to obtain a Form that has a symmetry compatible with 3-fold roto-inversion symmetry) means that we rotate the face 1200 clockwise about this axis (which here means about the vertical crystallographic axis) immediately followed by an inversion (of the rotation result) through the midpoint of the axis. The result will be a second face. If we now subject this new face to the same procedure a third face will be generated. In the same way a fourth, fifth and sixth face can be generated. When we continue this procedure after the sixth face has been generated no new faces will be generated anymore. The resulting configuration of faces -- the rhombohedron -- will automatically have the mirror planes and the 2-fold rotation axes as is indicated in the stereogram of the symmetry elements of the present Class (Figure 8).
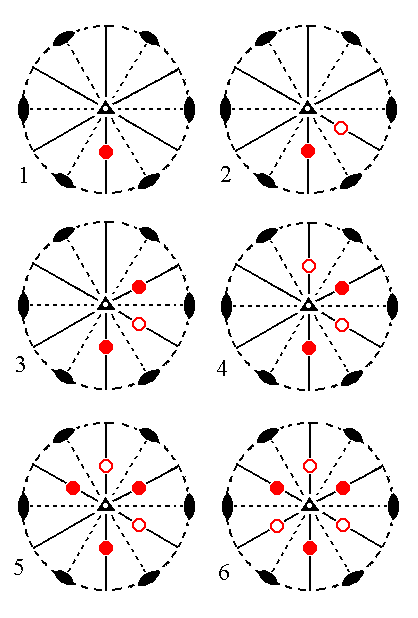 |
Figure 9. (1). Position of the face a : ~a : -a : c in the stereographic projection of the symmetry elements of the Ditrigonal-scalenohedric Crystal Class. (2). Generation of the second face. (3). Generation of the third face. (4). Generation of the fourth face. (5). Generation of the fifth face. (6). Generation of the sixth face. These six faces together make up the Rhombohedron. In (6) we can see that the remaining symmetry elements (three mirror planes and three 2-fold rotation axes) are implied. Solid disks (dots) represent upper ("northern") faces, small circles represent lower ("southern") faces . |
The face 2a : 2a : -a : c generates a Type II hexagonal bipyramid when subjected to the symmetry elements of the present Class. Let us first apply the 3-fold roto-inversion axis to this face. Figure 10 depicts the position of the face and the generation of a configuration of six faces by virtue of the action of the 3-fold roto-inversion axis (a* axis).
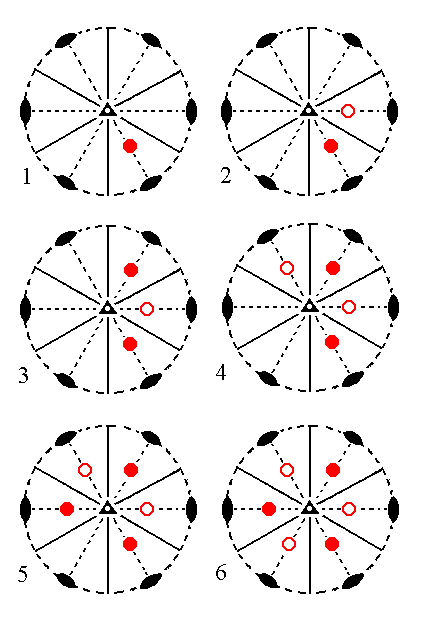 |
Figure 10. (1). Position of the face 2a : 2a : -a : c in the stereographic projection of the symmetry elements of the Ditrigonal-scalenohedric Crystal Class. (2). Generation of the second face. (3). Generation of the third face. (4). Generation of the fourth face. (5). Generation of the fifth face. (6). Generation of the sixth face. In (6) we can see that the remaining symmetry elements (three mirror planes and three 2-fold rotation axes) are NOT implied. |
In this Figure we see (in (6)) that the remaining symmetry elements of the Class are not implied, which means that the generated configuration of faces (in (6)) does not satisfy ALL the symmetry elements of the present Class. So we must continue our generation process : We subject each generated face in (6) to a 2-fold rotation. Such a 2-fold rotation generates from an upper face a second face which is a lower face, and it generates from a lower face a second face which is an upper face. So the stereogram of the final result shows six face pairs, each of which consists of an upper and a lower face, and the whole configuration of these faces constitutes a hexagonal bipyramid. The presence of upper and lower faces directly beneath each other should not however suggest the presence of an equatorial mirror plane : Although we obtain a BIpyramid, the top half is not symmetric with respect to the bottom half.
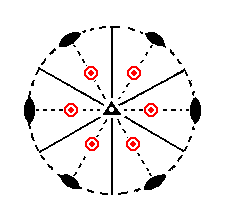 |
Figure 11. Stereogram of the rhombohedric hemihedric Type II Hexagonal Bipyramid, generated from the face 2a : 2a : -a : c, by subjecting it to the symmetry elements of the present Class. |
The face [3/2]a : 3a : -a : c is a definite face. Here we will consider its generalized version, namely the face [s/(s-1)]a : sa : -a : c. The position of this face in the stereogram of the symmetry elements of this Class is a general position, i.e. it does not have a special spatial relationship with respect to the symmetry elements and also not to the crystallographic axes. The corresponding Form, the ditrigonal scalenohedron (Figure 3h) is generated from this face as follows :
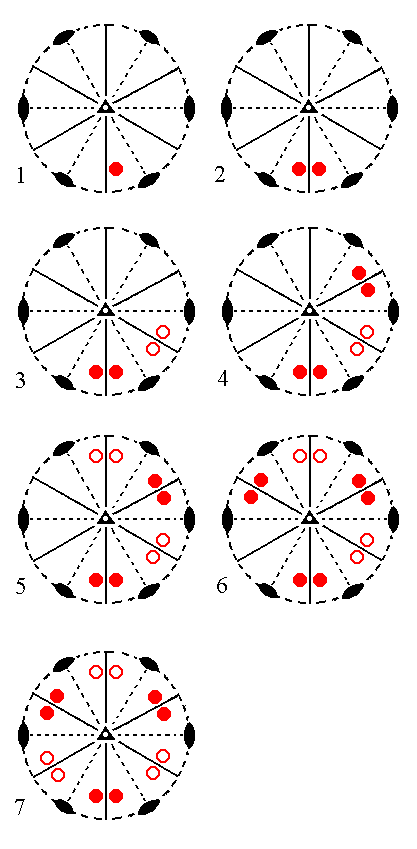 |
Figure 12. (1). Position of the face [s/(s-1)]a : sa : -a : c in the stereographic projection of the symmetry elements of the Ditrigonal-scalenohedric Crystal Class. (2). Generation of a second face in virtue of the nearby mirror plane, resulting in a face pair. (3). Generation of the second face pair in virtue of the 3-fold roto-inversion axis. (4). Generation of the third face pair by that same axis. (5). Generation of the fourth face pair. (6). Generation of the fifth face pair. (7). Generation of the sixth face pair, resulting in the Ditrigonal Scalenohedron, the general Form of the present Class. |
The face [3/2]a : 3a : -a : ~c is a definite face. Also in this case we will consider its generalized version [s/(s-1)]a : sa : -a : ~c. It is like the previous face, but now vertically oriented. Again the nearby mirror plane will generate a second face, resulting in a face pair, the members of which make an angle with each other of less than 1800, and are vertically orientated. When this face pair is subjected to the 3-fold roto-inversion axis five other vertical face pairs are generated. There is no distinction here between upper and lower faces because they are vertical. In the stereograms we denote these vertical faces with solid dots. So our final product is a set of six vertical face pairs, i.e. a (rhombohedric hemihedric) dihexagonal prism. The next Figure depicts the position of the face and the subsequent generation of the corresponding Form stereographically.
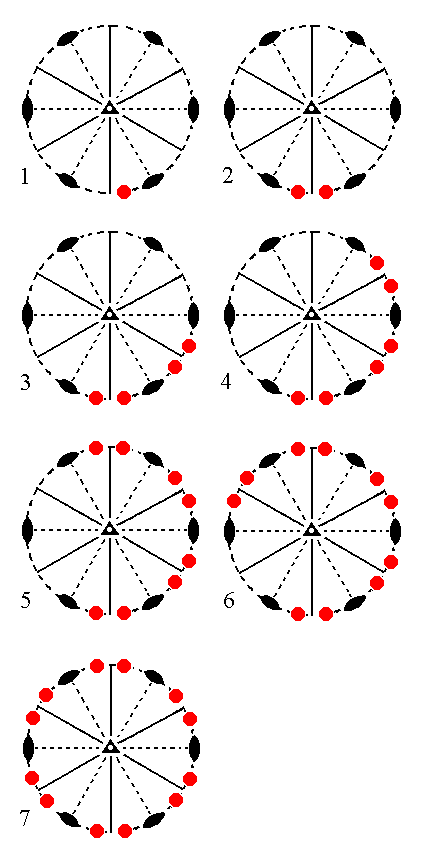 |
Figure 13. (1). Position of the face [s/(s-1)]a : sa : -a : ~c in the stereographic projection of the symmetry elements of the Ditrigonal-scalenohedric Crystal Class. (2). Generation of a second face in virtue of the nearby mirror plane, resulting in a face pair. (3). Generation of the second face pair in virtue of the 3-fold roto-inversion axis. (4). Generation of the third face pair by that same axis. (5). Generation of the fourth face pair. (6). Generation of the fifth face pair. (7). Generation of the sixth face pair, resulting in the Dihexagonal Prism. |
The face a : ~a : -a : ~c will generate a rhombohedric hemihedric Type I hexagonal prism, when it is subjected to the 3-fold roto-inversion axis. The remaining symmetries of the Class are then implied. See Figure 14.
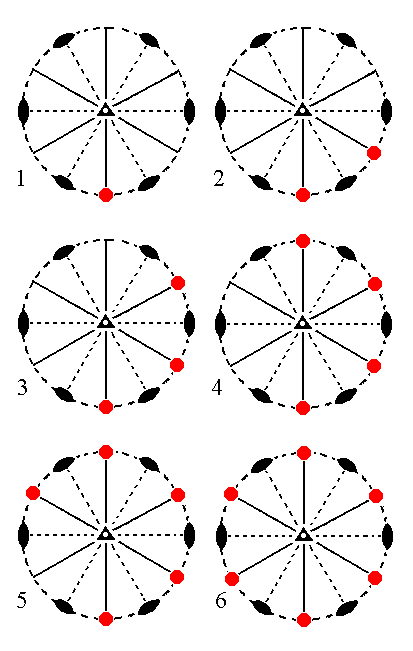 |
Figure 14. (1). Position of the face a : ~a : -a : ~c in the stereographic projection of the symmetry elements of the Ditrigonal-scalenohedric Crystal Class. (2). Generation of a second face in virtue of the 3-fold roto_inversion axis. (3). Generation of a third face, also in virtue of the 3-fold roto-inversion axis. (4). Generation of the fourth face by that same axis. (5). Generation of the fifth face. (6). Generation of the sixth face, (finally) resulting in the Type I Hexagonal Prism. |
The face 2a : 2a : -a : ~c will yield a rhombohedric hemihedric type II hexagonal prism when subjected to the symmetry elements of the Class : When we apply the action of the 3-fold roto-inversion axis to this face five new faces will be generated, resulting in the hexagonal prism. All remaining symmetries of the Class are then implied. See Figure 15.
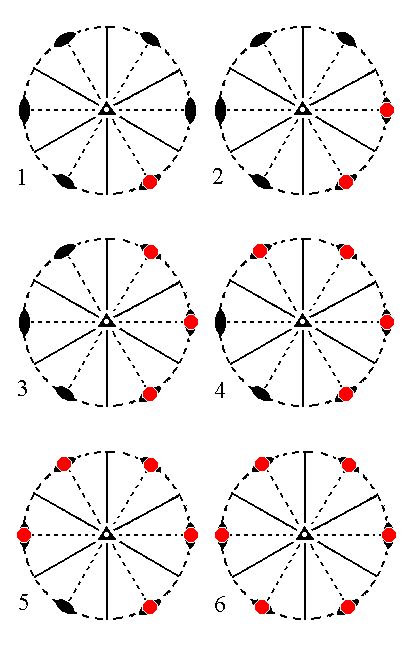 |
Figure 15. (1). Position of the face 2a : 2a : -a : ~c in the stereographic projection of the symmetry elements of the Ditrigonal-scalenohedric Crystal Class. (2). Generation of a second face in virtue of the 3-fold roto-inversion axis. (3). Generation of a third face, also in virtue of the 3-fold roto-inversion axis. (4). Generation of the fourth face by that same axis. (5). Generation of the fifth face. (6). Generation of the sixth face, (finally) resulting in the Type II Hexagonal Prism. |
Finally the face ~a : ~a : ~a : c, which is horizontal, generates a rhombohedric hemihedric basic pinacoid, when we subject it to the symmetry elements of the present Class : The rotational part of the 3-fold roto-inversion axis does not generate new positions from which to invert (through the midpoint of the axis), thus we can directly invert the face itself (through that point), resulting in a second face, parallel to the initial face. So we now have a parallel face pair consisting of an upper face and a lower face. The vertical mirror planes do not generate any new faces, and the same goes for the 2-fold rotation axes. Figure 16 depicts the position of the face and the generated basic pinacoid stereographically.
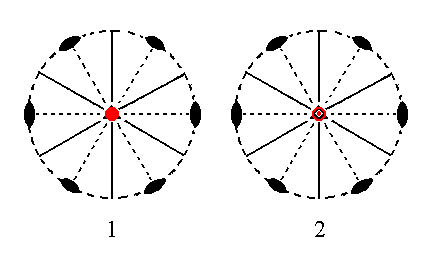
Figure 16.
(1). Position of the face ~a : ~a : ~a : c, in the stereographic projection of the symmetry elements of the Ditrigonal-scalenohedric Crystal Class.
(2). Stereogram of the rhombohedric hemihedric Basic Pinacoid [At the location of the 3-fold roto-inversion axis in the stereogram we now have two parallel horizontal faces (strictly, face poles), a lower one -- represented by a small red circle -- and an upper one -- represented by a red dot in the center of the small red circle].
This concludes our exposition of the Ditrigonal-scalenohedric Crystal Class.
To continue, klick HERE for Part Seven (Class 3* ).