The Hexagonal Crystal System (Part Seven)
back to homepage

back to Part One
back to Part Two
back to Part Three
back to Part Four
back to Part Five
back to Part Six

The Trigonal-rhombohedric Class
(= Rhombohedric Tetartohedric)   3*

This Class can be derived from the Rhombohedric Hemihedric Class (Division) (= the Ditrigonal-scalenohedric Class) by applying pyramidal hemihedric to its Forms. This means that in the Forms of the Rhombohedric Hemihedric Division we suppress all six vertical mirror planes. The symmetry elements of this Class are : In the Hermann-Maugin symbol for the symmetry of this Class the 3-fold rotation axis is given as a 3-fold roto-inversion axis (3*). This roto-inversion axis is however equivalent to a 3-fold rotation axis + center of symmetry.

Derivation of the Forms of the Trigonal-rhombohedric Class
(= Rhombohedric Tetartohedric)

MEROHEDRIC APPROACH.
The Forms of this Class will be found when we subject the rhombohedric hemihedric Forms one by one to the pyramidal hemihedric, which means that we suppress all the vertical mirror planes. Recall from Part Six that the rhombohedric hemihedric Forms of the Hexagonal Crystal System were the following :

Rhombohedron
Rhombohedric hemihedric Type II Hexagonal Bipyramid
Ditrigonal Scalenohedron
Rhombohedric hemihedric Type I Hexagonal Prism
Rhombohedric hemihedric Type II Hexagonal Prism
Rhombohedric hemihedric Dihexagonal Prism
Rhombohedric hemihedric Basic Pinacoid

From the Rhombohedron we will obtain again a rhombohedron, in fact two of them. They are rhombohedric tetartohedric Type I rhombohedra.
Let us explain how, by concentrating on horizontal sections. The Forms of this Class are -- as has been said -- derived by applying pyramidal hemihedric to rhombohedric hemihedric Forms.
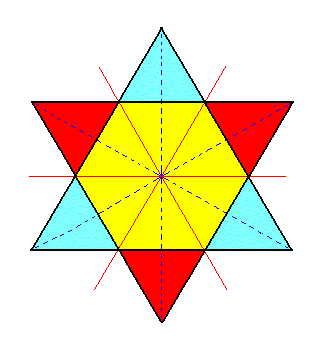
Recall from Part Six that -- in terms of horizontal sections -- a rhombohedron is derived by applying rhombohedric hemihedric to the holohedric protopyramid. See Figure 1.

  Figure 1. From two identical superimposed regular Hexagons we can derive two equilateral Triangles (regular Trigona) by alternately suppressing sides of one Hexagon (interpreted as the upper horizontal section through the Protopyramid) and allow the surviving sides to extend till they meet, and then do the same with the other Hexagon but with the whole process 600 rotated with respect to the first.
In the above Figure we have derived ONE rhombohedron. Here we could establish the blue triangle as representing the three upper faces of the rhombohedron, while the red triangle then represents the three lower faces of that same rhombohedron.
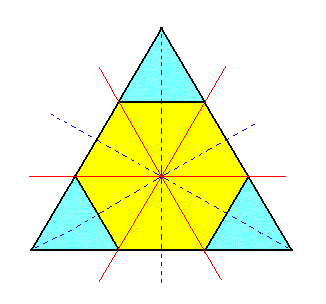A second rhombohedron can be derived by establishing the red triangle as representing the three upper faces of the rhombohedron, while the blue triangle then represents the three lower faces of the rhombohedron. These two rhombohedrons only differ in their orientation with respect to the crystallographic axes.
If we interpret Figure 1 as depicting not one but two rhombohedrons -- but then showing only one horizontal section of each of them, say of their upper part -- then we have depicted the two possible orientations for a Type I rhombohedron to have. One such rhombohedron, represented by a horizontal section through it, is depicted in Figure 1a.

  Figure 1a. Horizontal section through the upper part of a Type I Rhombohedron, derived by applying rhombohedric hemihedric to the holohedric Hexagonal Protopyramid.
Just the horizontal section of this rhombohedron (i.e. without the inscribed hexagon from which it is derived) is depicted in Figure 1b.

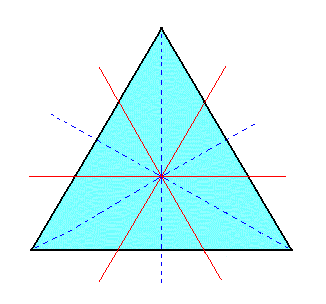  Figure 1b. Horizontal section through the upper part of a Type I Rhombohedron.
As can be seen in Figure 1b, mirror lines (representing mirror planes) are absent along the horizontal crystallographic axes (red lines), but still present between them.
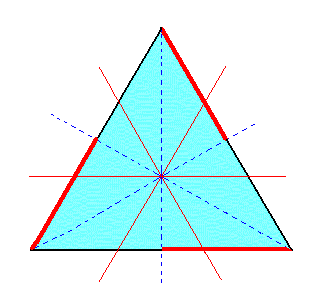To obtain the tetartohedric Form we must now apply to this rhombohedron pyramidal hemihedric, which boils down to dropping (i.e. suppressing) the rest of the mirror planes.
In our horizontal section we can visualize this (dropping) as follows (Figure 1c) :

  Figure 1c. Horizontal section through the upper part of a Type I Rhombohedron. The subsequent suppression of the mirror planes lying between the crystallographic axes is visualized by suppressing the relevant line segments (representing face areas) and allowing the remaining segments to extend. As can be seen the extension of those segments will restore the original triangle.
If we suppress the red segments in Figure 1c, expressing the suppression of the corresponding symmetry, and then allow the remaining segments (black) to extend till they meet, the original triangle will be recovered. This means that when we subject a type I rhombohedron (obtained from a holohedric protopyramid) to pyramidal hemihedric its external shape will not change, but its symmetry is lowered accordingly (by the loss of the mirror planes mentioned). One of the two possible rhombohedrons is depicted in Figure 1d.

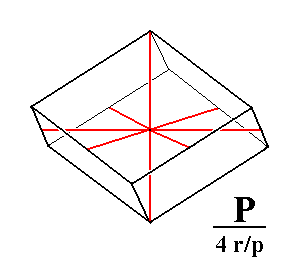  Figure 1d. Tetartohedric Type I Rhombohedron.
The expression "4 r/p" in the Naumann symbol means that (to the holohedric protopyramid (P)) a tetartohedric is applied, which in turn means that first a rhombohedric hemihedric is applied (to the holohedric Form), and to the result a pyramidal hemihedric.
From the rhombohedric hemihedric type II hexagonal bipyramid we can derive two type II rhombohedra. Also here we will explain this by using horizontal sections, and starting with the holohedric Form (to which first of all rhombohedric hemihedric is applied and then -- to the result -- pyramidal hemihedric. See Figure 2.

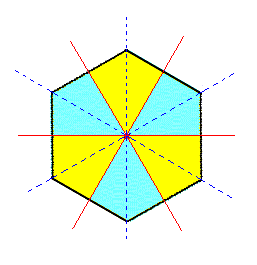  Figure 2. A regular Hexagon representing a horizontal section through the holohedric Deuteropyramid. As can be seen suppression of the mirror planes that go through the horizontal crystallographic axes (= rhombohedric hemihedric, as far as can be seen in a horizontal section) has no effect on the external shape. So the resulting rhombohedric hemihedric Form remains a Type II Hexagonal Bipyramid.
In Figure 2 we saw that the first hemihedric (the rhombohedric hemihedric) applied to the holohedric Deuteropyramid does not alter its shape, but of course its symmetry is lowered.
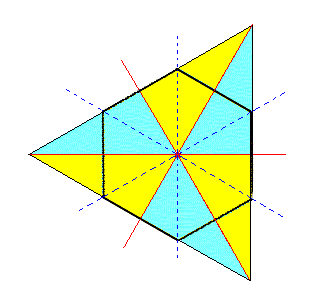Next we will apply to this result the pyramidal hemihedric, which means that the mirror planes situated between the crystallographic axes are suppressed. See Figure 2a.

  Figure 2a. By suppressing also the mirror planes lying between the horizontal crystallographic axes, we get -- by suppression and extension of the relevant line segments representing faces and symbolized by the coloring -- a triangle. This Triangle is a horizontal section through the tetartohedric rhombohedron (corresponding to the horizontal section through the Type II Bipyramid).
Figure 2a shows the derivation of a type II rhombohedron (represented by a horizontal section through it). In fact two such type II rhombohedrons are possible as Figure 2b shows.

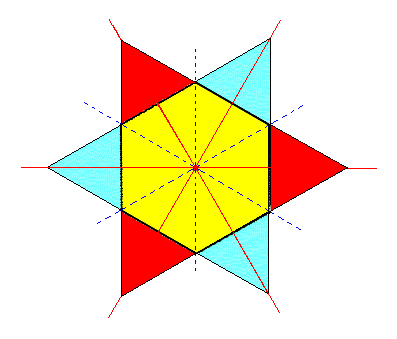  Figure 2b. Two Tetartohedric Type II Rhombohedra can be derived from the rhombohedric hemihedric Type II Hexagonal Bipyramid, shown in terms of horizontal sections.
From the Ditrigonal Scalenohedron we can derive four Type III rhombohedra.
To understand how, we first derive the dihexagon representing a horizontal section through the holohedric dihexagonal bipyramid (from which the scalenohedron is to be derived). This dihexagon can be derived from the superposition of two hexagons, one representing a horizontal section through the hexagonal protopyramid, the other through the hexagonal deuteropyramid. (The sections taken at corresponding heights above the equatorial plane).
In Part One we have learned how to construct these two hexagons. First we set up the hexagon representing the protopyramid. A second hexagon is constructed by rotatating the first by 300 (This second hexagon is not yet the hexagon that could represent the deuteropyramid). These two hexagons are depicted in Figure 3.

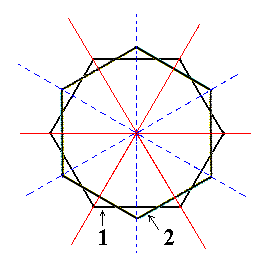  Figure 3. Superimposed horizontal sections through (1) the holohedric Protopyramid and (2) the image of its rotation by 300.
By enlarging the rotated hexagon as is done in the next Figure we obtain a hexagon that can represent the deuteropyramid (See for this, Part One).

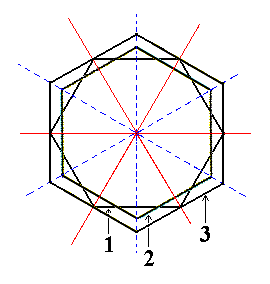  Figure 3a. Superimposed horizontal sections through (1) the holohedric Protopyramid, (2) the image of its rotation by 300, and (3) the Deuteropyramid.
The next Figure depicts the hexagon relating to the Protopyramid (1), and that relating to the Deuteropyramid (3).

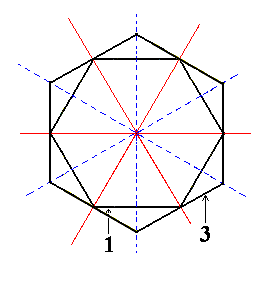  Figure 3b. Superimposed horizontal sections through (1) the holohedric Protopyramid, and (3) the holohedric Deuteropyramid. These sections could be interpreted as representing the equatorial planes of these pyramids, or as representing comparable horizontal sections somewhere through these pyramids.
We shall now construct a dihexagon (one of the many possible). Such a dihexagon is situated between the hexagon of the protopyramid and that of the deuteropyramid. See Figure 3c.

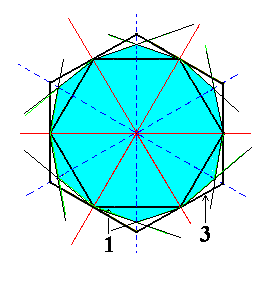  Figure 3c. Construction of a Dihexagon, representing a horizontal section through a Dihexagonal Bipyramid.
The resulting dihexagon is depicted in the next Figure.

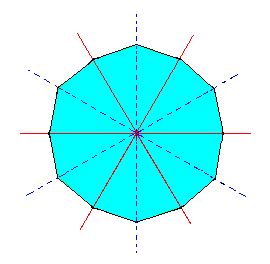  Figure 3d. A Dihexagon, representing a horizontal section through a Dihexagonal Bipyramid.
From this dihexagon we can derive the corresponding horizontal section through the ditrigonal scalenohedron by subjecting it to rhombohedric hemihedric, which for this horizontal section means that the mirror lines (representing mirror planes) that go through the horizontal crystallographic axes (red lines in the Figure) are suppressed. We can express this by the alternate suppression and extension of lines (representing faces), as Figure 3e shows.

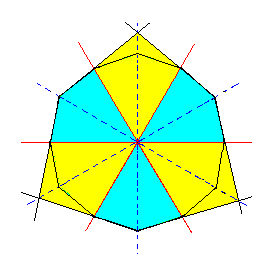  Figure 3e. Construction of a Ditrigon representing a horizontal section through a Ditrigonal Scalenohedron. Colors indicate the symmetries involved.
The resulting ditrigon is depicted in Figure 3f.

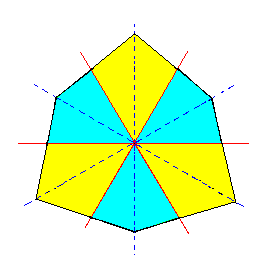  Figure 3f. A Ditrigon representing a horizontal section through a Ditrigonal Scalenohedron. Colors indicate the symmetries involved. One can clearly see that the mirror lines coinciding with the horizontal crystallographic axes (red lines) are absent (i.e. the corresponding mirror symmetry is absent), while it is still present in the lines bisecting the crystallographic axes (blue dashed lines). This is compatible with the symmetry of the rhombohedric hemihedric Forms.
From Figure 2h it is evident that actually two ditrigons can be constructed. The construction of the second possible ditrigon is depicted in Figure 3g.

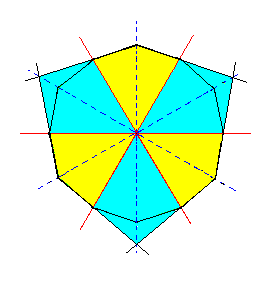  Figure 3g. Construction of a second Ditrigon representing a horizontal section through a second possible Ditrigonal Scalenohedron. Colors indicate the symmetries involved.
The constructed second Ditrigon is depicted in Figure 3h.

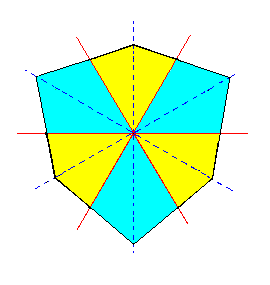  Figure 3h. A second Ditrigon representing a horizontal section through a second possible Ditrigonal Scalenohedron. Colors indicate the symmetries involved.
From each of these ditrigons a triangle (trigon) can be derived, by applying pyramidal hemihedric to them. This means that in the ditrigon the remaining mirror lines (representing mirror planes) are suppressed, as the next Figure shows. The resulting Triangle represents a horizontal section of a type III rhombohedron.

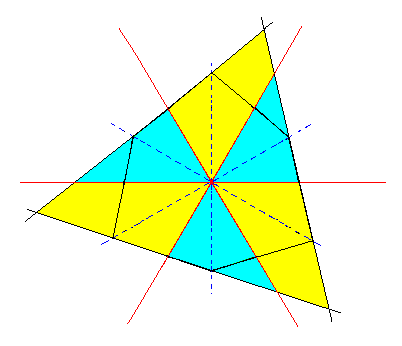  Figure 3i. Construction of a Triangle (trigon) from the Ditrigon of Figure 3f.
The resulting Triange is shown in Figure 3j.

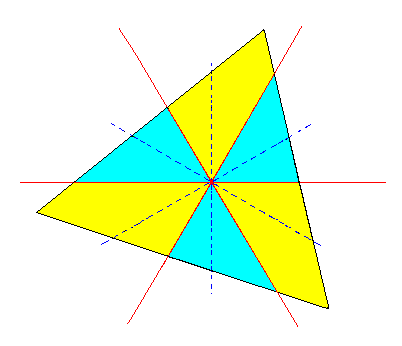  Figure 3j. A Triangle (trigon) constructed from the Ditrigon of Figure 3f. It is a horizontal section through the tetartohedric Type III Rhombohedron. The section must be imagined as being taken above the zig-zag line consisting of the middle edges of the Rhombohedron.
In Figure 3j the colors, symbolizing the symmetry, clearly show a 3-fold rotation axis. The three sides of the Triangle represent 3 faces of the rhombohedron. Below these faces lie three others -- separated from the upper three by six zig-zag going edges. The lower faces can, like the upper faces, be represented by a triangle. This second triangle is 600 rotated with respect to the first. This means that for each upper face there is a lower face parallel to it, and this is the same as saying that the whole configuration of faces has a center of symmetry. Well, a 3-fold rotation axis and a center of symmetry together form a 3-fold roto-inversion axis, and this -- having just a 3-fold roto-inversion axis -- is precisely the symmetry (content) of our Class.

As can be surmised from Figure 2l, actually two Triangles can be derived. See Figures 3k and 3l.

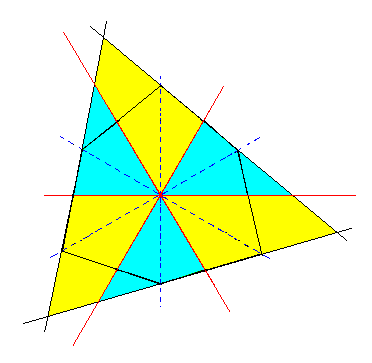  Figure 3k. Construction of a second Triangle (trigon) from the Ditrigon of Figure 3f.
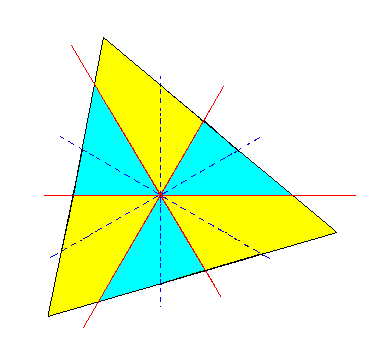  Figure 3l. A second Triangle (trigon) constructed from the Ditrigon of Figure 3f. It is a horizontal section through a tetartohedric Type III Rhombohedron. The section must be imagined as being taken above the zig-zag line consisting of the middle edges of the Rhombohedron.
In exactly the same way we can derive two Triangles from the second possible ditrigon, namely the one depicted in Figure 3h. So all in all we can derive four type III tetartohedric rhombohedra, from one holohedric dihexagonal pyramid : first -- by applying rhombohedric hemihedric -- two ditrigonal scalenohedra, and then -- applying pyramidal hemihedric to these scalenohedra -- four type III tetartohedric rhombohedra.

The derivation of the rhombohedra from scalenohedra was shown in terms of horizontal sections representing the complete Forms. To complete our exposition of this derivation we will now show the complete scalenohedron, and how it gives rise to rhombohedrons when subjected to pyramidal hemihedric.

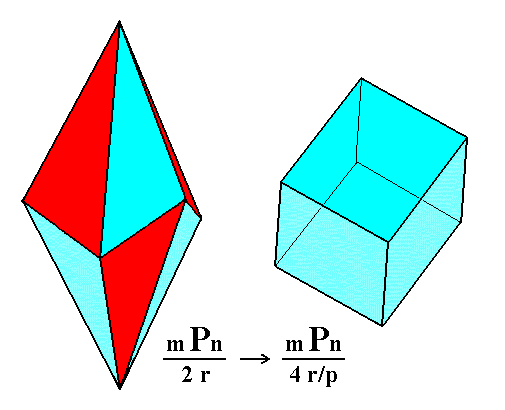
Figure 3m. Derivation of a Type III Rhombohedron from (the white faces of) a Ditrigonal Scalenohedron.
Only the shapes of the respective Forms (Scalenohedron, Rhombohedron) are given. They are not necessarily drawn at precisely the same scale.
From the rhombohedric hemihedric type I hexagonal prism we can derive the rhombohedric tetartohedric type I hexagonal prism, by subjecting it to the pyramidal hemihedric (this is equivalent to saying that we subject the holohedric protoprism to rhombohedric tetartohedric).

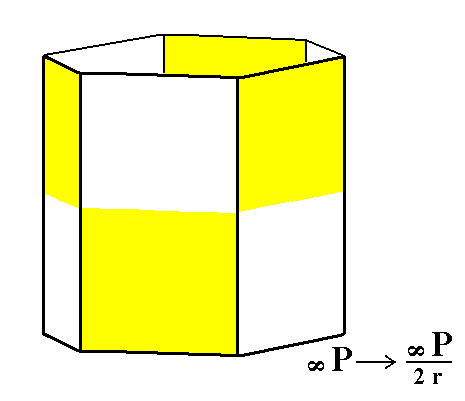
Figure 4. The rhombohedric hemihedric Type I Hexagonal Prism, from which the rhombohedric tetartohedric Type I Hexagonal Prism can be derived (Figure 4a).

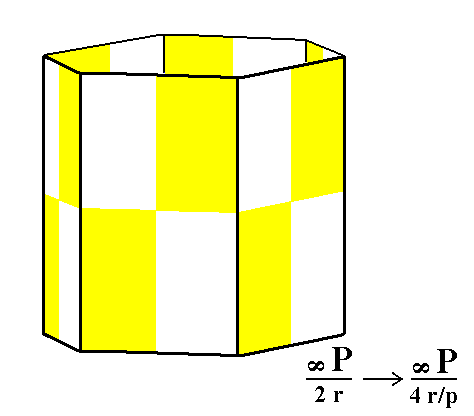
Figure 4a. The rhombohedric tetartohedric Type I Hexagonal Prism.

As can be seen from the Figure, the external shape will not change, the generated Form is still a hexagonal prism, but with lowered symmetry.

From the rhombohedric hemihedric type II hexagonal prism we can derive the rhombohedric tetartohedric type II hexagonal prism, when we subject it to the pyramidal hemihedric. See Figures 5 and 5a.

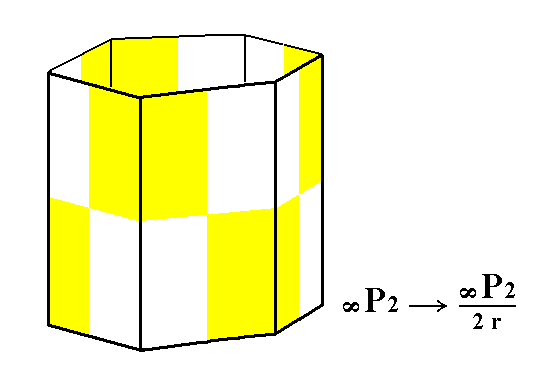
Figure 5. The rhombohedric hemihedric Type II Hexagonal Prism, from which the rhombohedric tetartohedric Type II Hexagonal Prism will be derived (Figure 5a).

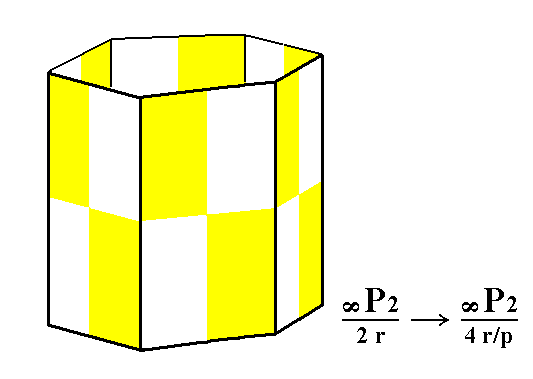
Figure 5a. The rhombohedric tetartohedric Type II Hexagonal Prism.

As can be seen from the Figure, the external shape will not change. The generated Form remains a hexagonal prism.

From the rhombohedric hemihedric dihexagonal prism we can derive the rhombohedric tetartohedric type III hexagonal prism (in fact two of them), when we subject it to pyramidal hemihedric. See Figures 6 and 6a.

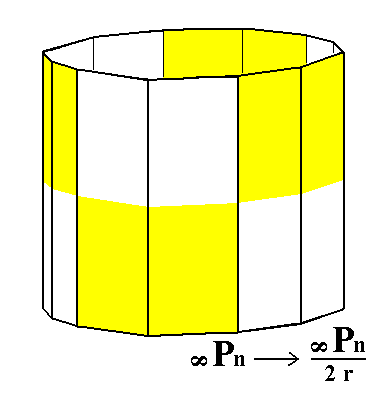
Figure 6. The rhombohedric hemihedric Dihexagonal Prism, from which the rhombohedric tetartohedric Type III Hexagonal Prism will be derived (Figure 6a).

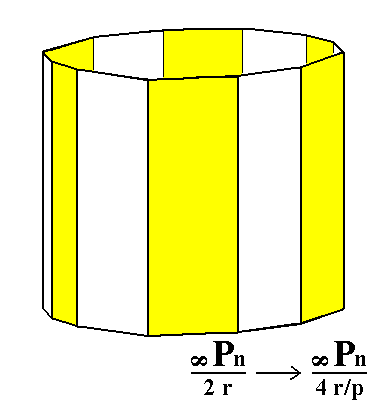
Figure 6a. The rhombohedric tetartohedric Type III Hexagonal Prism.
By suppressing the yellow faces and letting the others extend till they meet (in order to express the application of pyramidal hemihedric) we will obtain a hexagonal prism. Another such prism will be obtained when we suppress all the white faces and let the others extend till they meet.

To express the loss of the equatorial mirror plane (by virtue of the rhombohedric hemihedric) we could perhaps better depict the derivation of the rhombohedric tetartohedric type III hexagonal prism as is done in the next Figure :

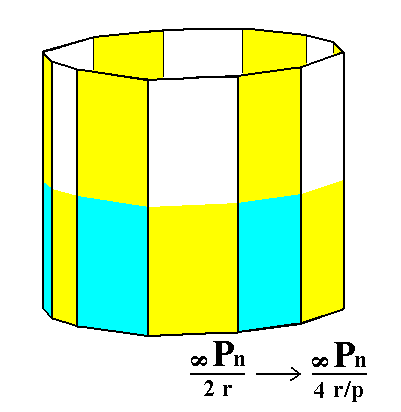
Figure 6b. By suppressing all areas except the white ones, and letting these extend till they meet (in order to express pyramidal hemihedric to be applied) we will obtain a rhombohedric tetartohedric Type III Hexagonal Prism. A second rhombohedric tetartohedric Type III Hexagonal Prism will be obtained when we suppress all the areas except the blue ones and let these extend till they meet.
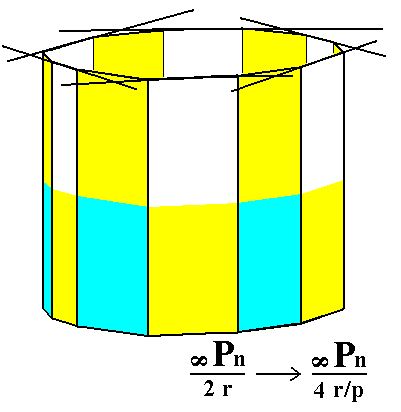  Figure 6c. Construction of the rhombohedric tetartohedric Type III Hexagonal Prism from a rhombohedric hemihedric Dihexagonal Prism. See Figure 6d.
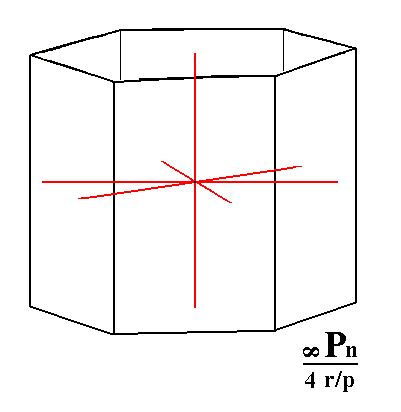  Figure 6d. A rhombohedric tetartohedric Type III Hexagonal Prism, and its orientation with respect to the four crystallographic axes.
Finally, from the rhombohedric hemihedric basic pinacoid we can derive the rhombohedric tetartohedric basic pinacoid when we subject it to pyramidal hemihedric (= equivalent to subjecting the holohedric basic pinacoid to rhombohedric tetartohedric). Figure 7 depicts the rhombohedric hemihedric basic pinacoid.

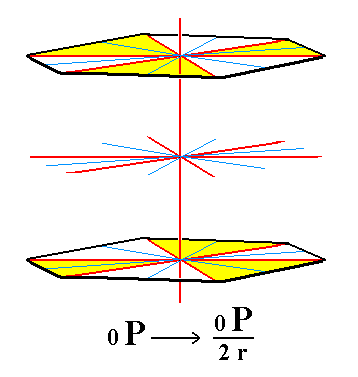  Figure 7. The rhombohedric hemihedric basic pinacoid, from which the rhombohedric tetartohedric basic pinacoid will be derived by suppressing the remaining mirror planes (Figure 7a).
As can be seen from Figure 7a the suppression of the mirror planes does not alter the shape of the resulting Form (no faces disappear), it remains a basic pinacoid, i.e. a Form consisting of two horizontal parallel faces, but its symmetry is lowered accordingly. See Figure 7a.

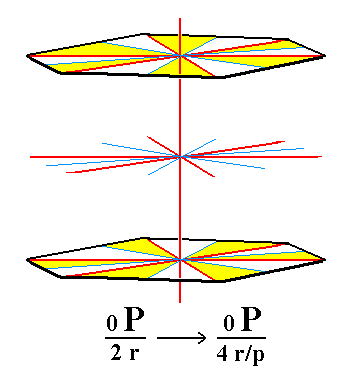  Figure 7a. The rhombohedric tetartohedric Basic Pinacoid.
This concludes our derivation of all the Forms of this Class by means of the Merohedric Approach.

All these Forms can engage in combinations with each other in real crystals.
FACIAL APPROACH

We will now derive those same Forms by subjecting the basic faces (compatible with the Hexagonal Crystal System) one by one to the symmetry operations of the present Class (the Trigonal-rhombohedric Crystal Class).
In Part One we found the following seven basic faces compatible with the Hexagonal Crystal System :

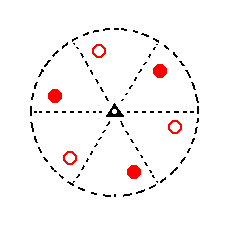The stereographic projection of the symmetry elements of this Class is given in Figure 8.

  Figure 8. Stereogram of the symmetry elements of the Trigonal-rhombohedric Crystal Class, and of all the faces of the most general Form.
The face a : ~a : -a : c generates a type I rhombohedric tetartohedric rhombohedron when subjected to the symmetry elements of the present Class, which here means that we subject it to the workings of the 3-fold roto-inversion axis, which is the only symmetry element of the Class. The face will be rotated clockwise 1200 and the preliminary result directly inverted through the midpoint of the axis. This rotation + inversion is one action, and generates one new face. Then this same procedure will be applied to that new face, resulting in a third face. After five times no new faces are generated anymore. The result is a Form consisting of three pairs of parallel faces forming a type I rhombohedron. See Figure 9.

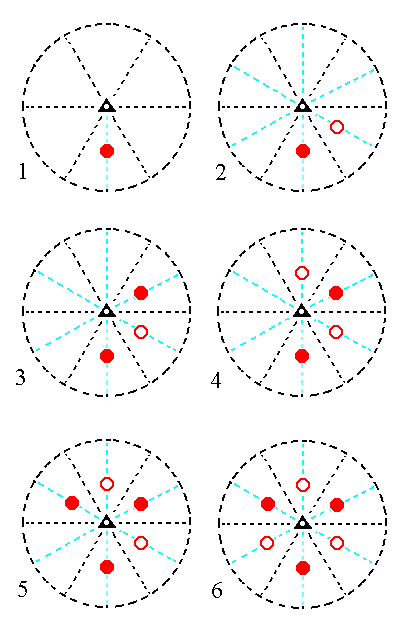  Figure 9.
(1). Position of the face
a : ~a : -a : c in the stereographic projection of the symmetry elements of the Trigonal-rhombohedric Crystal Class.
(2). Generation of the second face.
(3). Generation of the third face.
(4). Generation of the fourth face.
(5). Generation of the fifth face.
(6). Generation of the sixth face, completing the generation of a Type I Rhombohedron.
Solid dots represent upper faces, small circles represent lower faces.
If we had started with a lower face, namely the face a : ~a : -a : -c (thus, -c instead of c), then we would end up with the second possible type I rhombohedron :

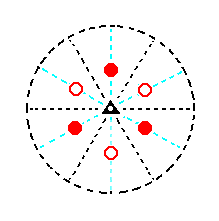  Figure 10. Stereogram of the second possible Type I Rhombohedron.
The face 2a : 2a : -a : c generates a type II rhombohedron when subjected to the symmetry elements of the present Class (Recall that the only symmetry element of the Class is a 3-fold roto-inversion axis). See Figure 11.

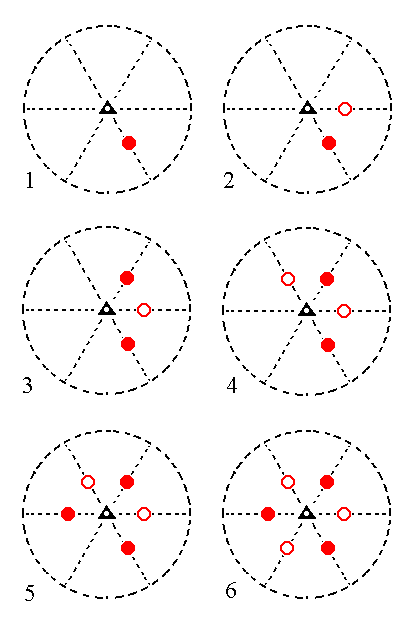  Figure 11.
(1). Position of the face
2a : 2a : -a : c in the stereographic projection of the symmetry elements of the Trigonal-rhombohedric Crystal Class.
(2). Generation of the second face.
(3). Generation of the third face.
(4). Generation of the fourth face.
(5). Generation of the fifth face.
(6). Generation of the sixth face, completing the generation of a Type II Rhombohedron.
Solid dots represent upper faces, small circles represent lower faces.
The second type II rhombohedron can be found in the same way as we did with respect to the type I rhombohedron.

The face [3/2]a : 3a : -a : c is a definite face. We will consider here a generalized version of it, namely the face [s/(s-1)]a : sa : -a : c. From this face we can generate a type III rhombohedron, by subjecting it to the symmetry elements of the present Class.

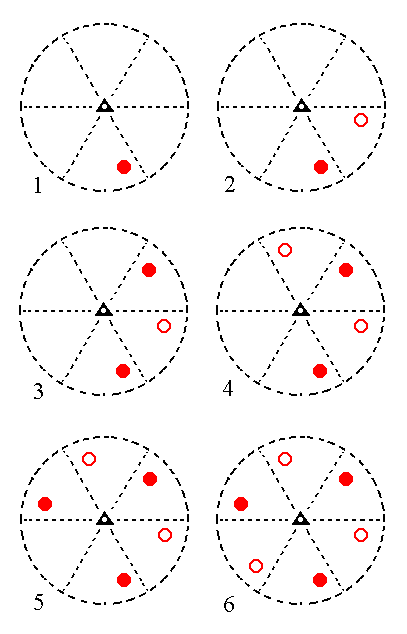  Figure 12.
(1). Position of the face
[s/(s-1)]a : sa : -a : c in the stereographic projection of the symmetry elements of the Trigonal-rhombohedric Crystal Class.
(2). Generation of the second face.
(3). Generation of the third face.
(4). Generation of the fourth face.
(5). Generation of the fifth face.
(6). Generation of the sixth face, completing the generation of a Type III Rhombohedron.
Solid dots represent upper faces, small circles represent lower faces.
In fact four type III rhombohedrons can be generated, depending on the (choice of) starting face. The next Figure shows these four possible rhombohedrons.

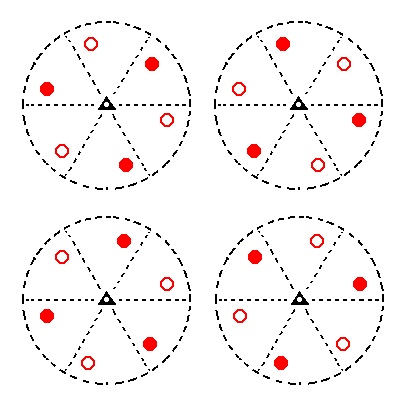  Figure 13. Stereograms of the four possible Type III Rhombohedrons.
The face [3/2]a : 3a : -a : ~c is a definite face. Here we will consider a generalized version of it, namely the face [s/(s-1)]a : sa : -a : ~c. It is like the previous face, except that it is vertical. When we subject this face to the symmetry elements of the present Class we will generate a rhombohedric tetartohedric type III hexagonal prism. Because the face is vertical there will be no difference between upper and lower faces. They are signified by solid dots. See Figure 14.

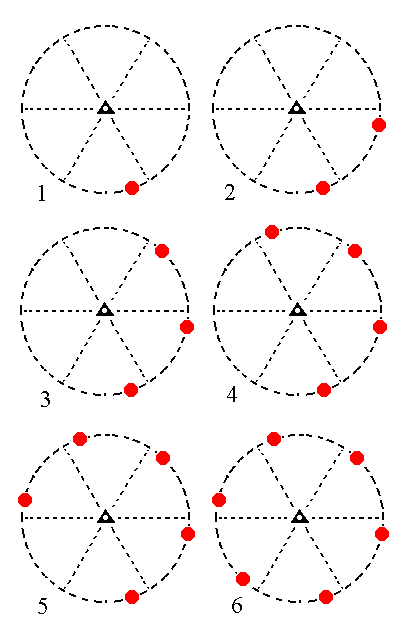  Figure 14.
(1). Position of the face
[s/(s-1)]a : sa : -a : ~c in the stereographic projection of the symmetry elements of the Trigonal-rhombohedric Crystal Class.
(2). Generation of the second face.
(3). Generation of the third face.
(4). Generation of the fourth face.
(5). Generation of the fifth face.
(6). Generation of the sixth face, completing the generation of a Type III Hexagonal Prism.
A second possible rhombohedric tetartohedric type III hexagonal prism can be derived, starting with another face. This prism is depicted stereographically in Figure 15.

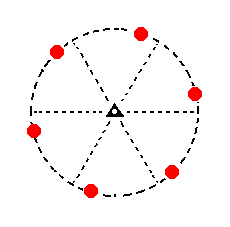  Figure 15.
Stereogram of the second possible rhombohedric tetartohedric Type III Hexagonal Prism.
The face a : ~a : -a : ~c generates a type I hexagonal prism, when subjected to the symmetry elements of the Class. The 3-roto-inversion axis will generate six vertical faces. See Figure 16.

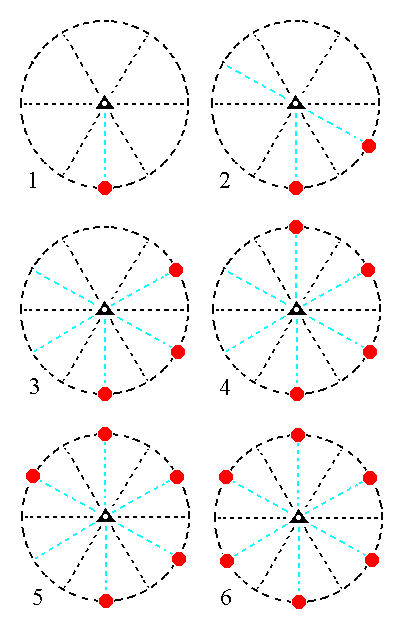  Figure 16.
(1). Position of the face
a : ~a : -a : ~c in the stereographic projection of the symmetry elements of the Trigonal-rhombohedric Crystal Class.
(2). Generation of the second face.
(3). Generation of the third face.
(4). Generation of the fourth face.
(5). Generation of the fifth face.
(6). Generation of the sixth face, completing the generation of a Type I Hexagonal Prism.
The face 2a : 2a : -a : ~c will generate a type II hexagonal prism : When we subject that face to the workings of the 3* axis it will be multiplied six times around that axis, as Figure 17 shows stereographically.

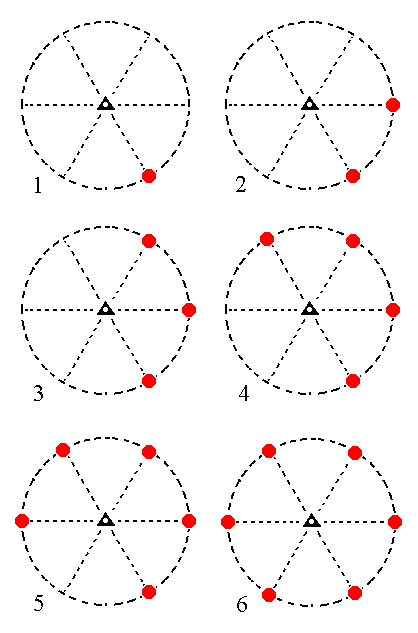  Figure 17.
(1). Position of the face
2a : 2a : -a : ~c in the stereographic projection of the symmetry elements of the Trigonal-rhombohedric Crystal Class.
(2). Generation of the second face.
(3). Generation of the third face.
(4). Generation of the fourth face.
(5). Generation of the fifth face.
(6). Generation of the sixth face, completing the generation of a Type II Hexagonal Prism.
Finally, the face ~a : ~a : ~a : c is horizontal. The rotational part of the action of the 3* axis does not have any effect [ i.e. it doesn't bring the face (first) to another location -- from which subsequent inversion will take place resulting in a new face ], so only the inversion part of the action of that axis will generate new faces. In the present case it will generate one new face parallel to our starting face. This means that a basic pinacoid is formed. See Figure 18, which depicts this stereographically.

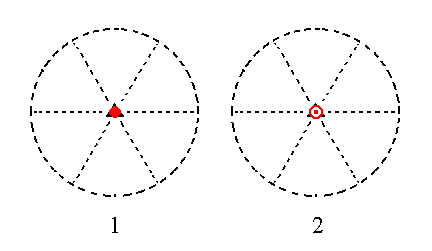
Figure 18.
(1). Position of the face ~a : ~a : ~a : c in the stereographic projection of the symmetry elements of the Trigonal-rhombohedric Crystal Class.
(2). Generation of the second face, completing the generation of the Basic Pinacoid.

This concludes our exposition of the Trigonal-rhombohedric Crystal Class.
To continue, klick HERE for Part Eight (Class 6* m 2 ).

back to homepage

back to Part One

back to Part Two

back to Part Three

back to Part Four

back to Part Five

back to Part Six

****************