back to homepage
back to Part One
back to Part Two
back to Part Three
back to Part Four
back to Part Five
back to Part Six
back to Part Seven
Protopyramid (= hexagonal type I bipyramid)
Deuteropyramid (= hexagonal type II bipyramid)
Dihexagonal Bipyramid
Protoprism (= hexagonal type I prism)
Deuteroprism (= hexagonal type II prism)
Dihexagonal Prism
Basic Pinacoid
From the holohedric protopyramid we can derive two trigonal bipyramids by subjecting this Form to trigonal hemihedric, which means that we suppress the three vertical mirror planes that go through the three horizontal crystallographic axes. This can be expressed by alternately suppressing face pairs consisting of an upper and a lower face.
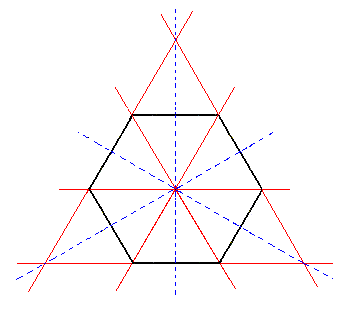
Figure 1 shows this by means of depicting the equatorial plane. Figure 1a shows the partition of the whole pyramid. Figure 1b shows the construction of the trigonal bipyramid and Figure 1c shows the resulting trigonal bipyramid.
 |
Figure 1. From the equatorial plane of the holohedric Hexagonal Protopyramid can be constructed the equatorial plane of the Trigonal Bipyramid, by alternate suppression and extension of its sides. Two such equatorial planes can in fact be constructed, depending on which sides are allowed to survive and extend. |
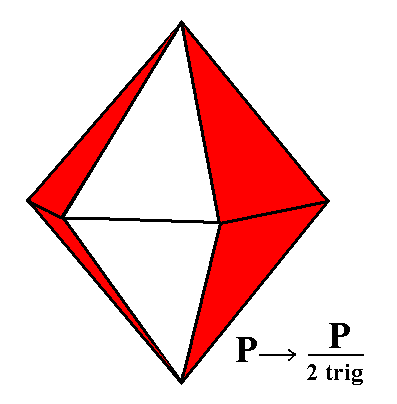 |
Figure 1a. From the holohedric Hexagonal Protopyramid can be constructed the Trigonal Bipyramid, by alternate suppression and extension of its faces. Two such Trigonal Bipyramids can in fact be constructed, depending on which sides are allowed to survive and extend. One is depicted in Figure 1c. The symbol "trig" in the expression "2 trig" of the Naumann symbol means that trigonal hemihedric is being applied. |
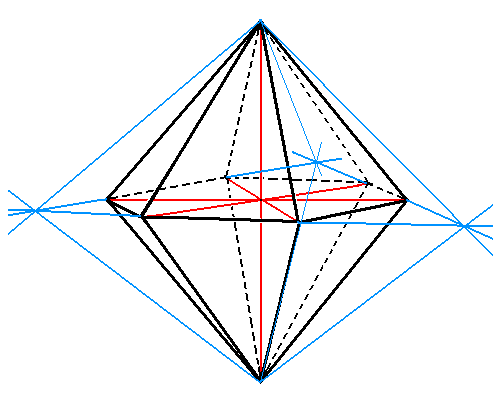
Figure 1b. Construction of the Trigonal Bipyramid from the white faces of the (partitioned) Protopramid of Figure 1a.
A second Trigonal Bipyramid can be constructed from the red faces.
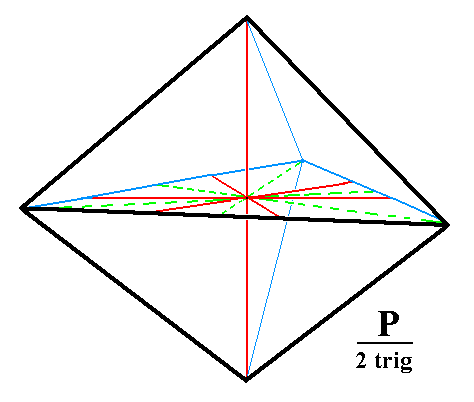
Figure 1c. A Trigonal Bipyramid, and its orientation with respect to the four crystallographic axes (red lines).
From the holohedric deuteropyramid (= hexagonal type II bipyramid) a trigonal hemihedric type II hexagonal bipyramid can be derived, by subjecting it to trigonal hemihedric. As can be seen in Figure 2 its external shape does not change, but its symmetry is lowered accordingly.
 |
Figure 2. From the holohedric Hexagonal Deuteropyramid can be derived the trigonal hemihedric Type II Hexagonal bipyramid. There is no loss of faces, so the external shape remains the same.
The symbol "trig" in the expression "2 trig" of the Naumann symbol means that trigonal hemihedric is being applied. |
From the holohedric dihexagonal bipyramid two ditrigonal bipyramids can be derived when we apply trigonal hemihedric to it. The effect of the suppression of the vertical mirror planes that go through the horizontal crystallographic axes is depicted in terms of the equatorial plane and of the whole pyramid in the next Figures.
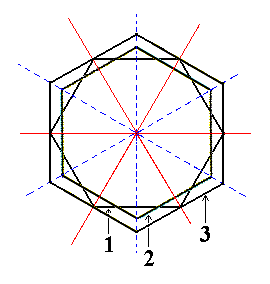 |
Figure 3. Superimposed equatorial planes through (1) the holohedric Protopyramid, (2) the image of its rotation by 300, and (3) the Deuteropyramid. The possible dihexagons (representing the equatorial planes of the possible Dihexagonal Bipyramids) lie between that of the Protopyramid and that of the Deuteropyramid. |
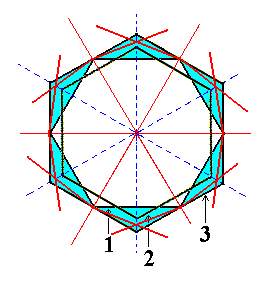 |
Figure 3a. Construction of a Dihexagon, representing a Dihexagonal Bipyramid. |
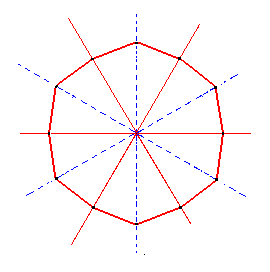 |
Figure 3b. A Dihexagon, representing a Dihexagonal Bipyramid. |
From the dihexagon of Figure 3b we will derive two ditrigons which can stand for the equatorial planes of the two possible ditrigonal bipyramids.
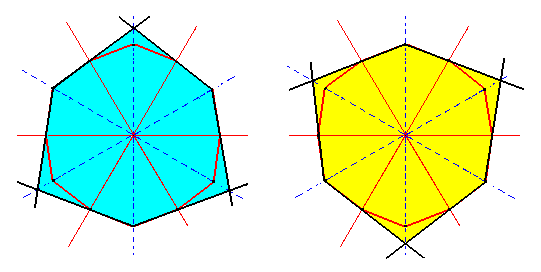
Figure 3c. Construction of the two Ditrigons that can be derived from the dihexagon of Figure 3b.
The dihexagon used here was constructed in Figure 3a. From this Figure it is evident that many different dihexagons can be constructed. In order to illustrate this we will construct another variant of the dihexagon, also of course situated between the outlines of the equatorial planes of the protopyramid and of the deuteropyramid, but now differently positioned (between them)-- compare Figure 3a and 3d.
In deriving the possible Forms from the holohedric dihexagonal bipyramid we will use this latter variant of the dihexagon (representing the equatorial plane of that bipyramid) because, as will be seen, the ditrigons that derive from it show more clearly their trigonal aspect (i.e. their shape approaches that of a triangle (= trigon)).
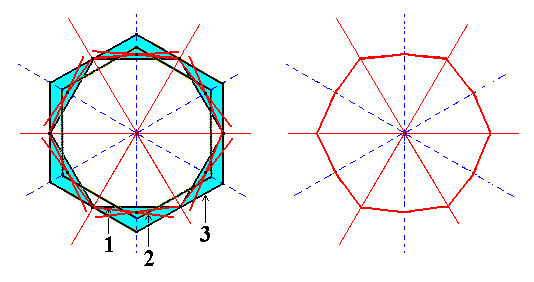
Figure 3d. Construction of another possible dihexagon, by choosing another point within the range of possible dihexagons (this range is indicated in this Figure and in Figure 3a by means of blue coloring).
From the dihexagon, constructed in Figure 3d, we will now derive the two possible ditrigons by alternately suppressing side pairs and letting extend the others. See figure 3e.
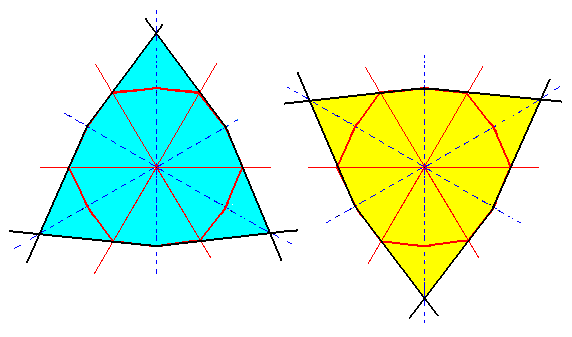
Figure 3e. Construction of the two possible Ditrigons from the dihexagon of Figure 3d.
The trigonal aspect is clearly expressed. The result of the first construction is depicted in Figure 3f.
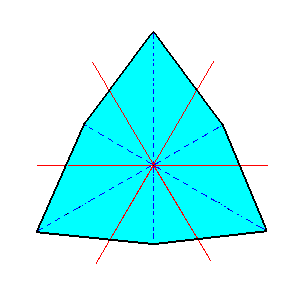 |
Figure 3f. A Ditrigon, representing a Ditrigonal Bipyramid. We can clearly see that the mirror lines (representing mirror planes) going through the horizontal crystallographic axes (red lines) are absent, and that the mirror lines (representing mirror planes) that bisect the angles between the horizontal crystallographic axes are still present, as demanded by trigonal hemihedric. |
In the next figure we will finally depict the derivation of the whole ditrigonal bipyramid (that has a ditrigon as its equatorial plane) from the holohedric dihexagonal bipyramid.
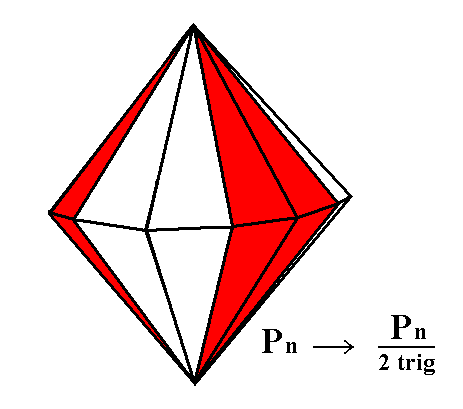
Figure 3g. Merohedric derivation of the Ditrigonal Bipyramid from the holohedric Dihexagonal Bipyramid. Two such Ditrigonal Pyramids are possible depending on which face pairs are suppressed (while letting the others extend till they meet). The result is depicted in Figure 3h.
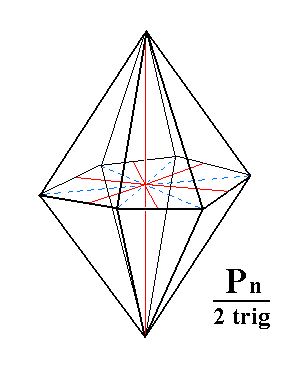 |
Figure 3h. A Ditrigonal Bipyramid, derived from the white faces of the pyramid of Figure 3g. Not necessarily drawn on the same scale (which implies that we could imagine a parameter different from 1 (put) in front of the P of the Naumann symbol). |
Of course the ditrigonal bipyramid is just a hexagonal bipyramid, but its equatorial plane is not a regular hexagon. Although its sides are equal, its corners represent two angles, three equal more or less obtuse angles and three equal more acute angles (See Figure 3f or 3c).
The above figure clearly shows the equality of the horizontal edges (bordering the equatorial plane). The next Figures show ditrigonal bipyramids where the inequality of the corners of the ditrigon (equatorial plane) is clearly pronounced (Recall that several dihexagons are possible and consequently several possible ditrigons -- and so several corresponding ditrigonal bipyramids).
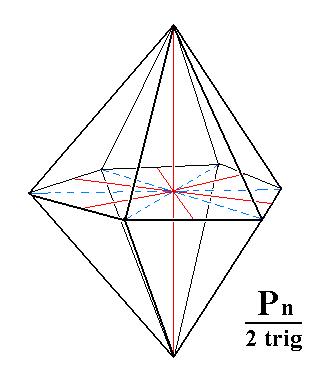 |
Figure 3i. Another possible Ditrigonal Bipyramid. |
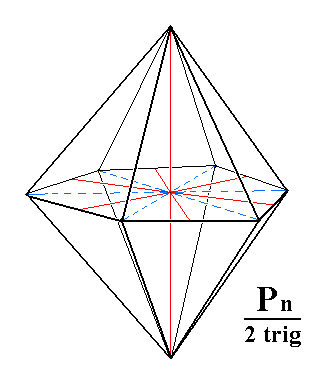 |
Figure 3j. Another possible Ditrigonal Bipyramid. |
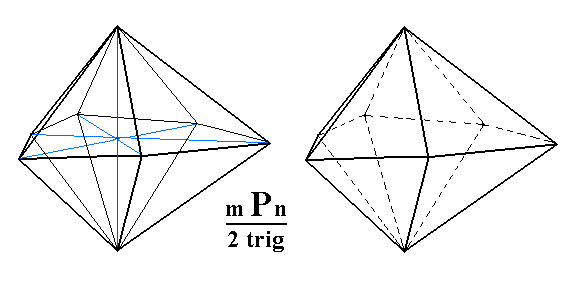
Figure 3k. Yet another Ditrigonal Bipyramid.
Left image drawn with main crystallographic axis and bisectors of the horizontal crystallographic axes. The trigonal aspect is well expressed (i.e. the ditrigonal pyramid approaches a trigonal pyramid).
From the holohedric protoprism (= hexagonal type I prism) we can derive the trigonal prism when we subject it to trigonal hemihedric. In fact two such trigonal prisms are possible. See the following Figures.
Let us first expound the generation of this Form (the trigonal prism) in terms of horizontal sections. Suppressing the mirror planes that go through the horizontal crystallographic axes can be expressed by alternate suppression of the sides of a regular hexagon (representing a horizontal section through a protoprism). See Figure 4.
 |
Figure 4. From a horizontal section through the holohedric Hexagonal Protoprism can be constructed the corresponding horizontal section through the Trigonal Prism, by alternate suppression and extension of its sides. Two such horizontal sections can in fact be constructed, depending on which sides are allowed to survive and extend. The red diagonal lines converging in a common point are the horizontal crystallographic axes. |
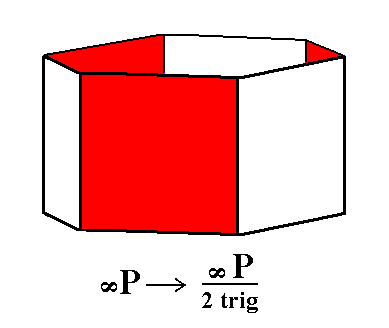 |
Figure 4a. Generation of the Trigonal Prism from the holohedric Hexagonal Protoprism. Two Trigonal Prisms are possible, depending on which faces are suppressed (and the others allowed to extend till they meet). |
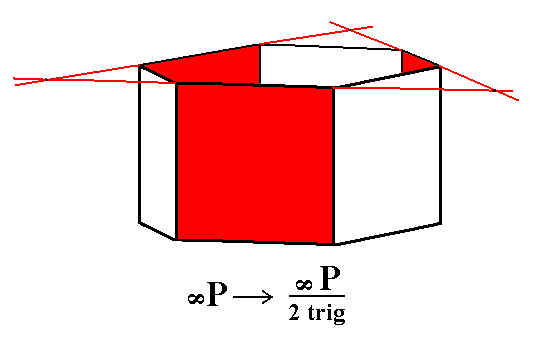
Figure 4b. Construction of a Trigonal Prism from the red faces of the Protoprism.
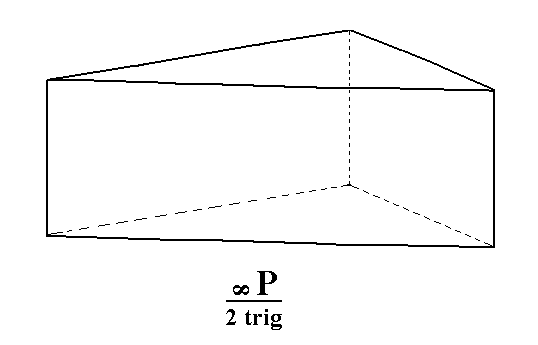
Figure 4c. A Trigonal Prism from the red faces of the Protoprism of Figure 4a.
From the holohedric deuteroprism (= hexagonal type II prism) we can derive the trigonal hemihedric type II hexagonal prism when we subject it to trigonal hemihedric. As can be seen in the next Figure the new Form will have the same external shape as the holohedric deuteroprism.
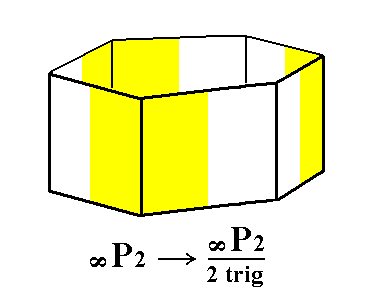 |
Figure 5. The holohedric Deuteroprism retains its shape when subjected to trigonal hemihedric. |
From the holohedric dihexagonal prism we can derive the ditrigonal prism, when we apply trigonal hemihedric to it. The next Figure illustrates the derivation in terms of a horizontal section.

Figure 6. Derivation of two Ditrigons from a horizontal section through the holohedric Dihexagonal Prism. The red diagonal lines are the horizontal crystallographic axes.
The next Figure shows the whole holohedric Dihexagonal Prism and its partition according to trigonal hemihedric.
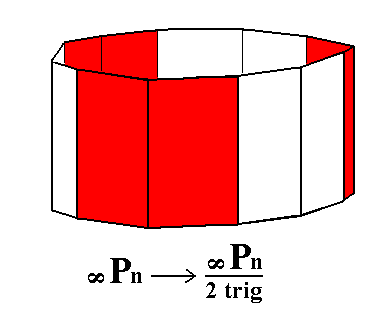 |
Figure 6a. Partition of the holohedric Dihexagonal Prism. Two possible Ditrigonal Prisms can be derived, depending on which face pairs are suppressed (and the remaining ones allowed to extend till they meet). |
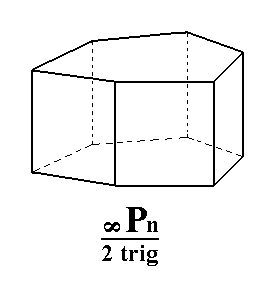 |
Figure 6b. A Ditrigonal Prism, derived from the red faces of the Dihexagonal Prism of Figure 6a. |
From the holohedric basic pinacoid we can derive the trigonal hemihedric basic pinacoid when we subject it to trigonal hemihedric. The external shape will remain the same, i.e. our new Form still consists of two parallel horizontal faces. Like the prisms it is an open Form, which means that it can exist in real crystals only in combination with other Forms of this Class that cause it to be closed. Figure 7 depicts this pinacoid.
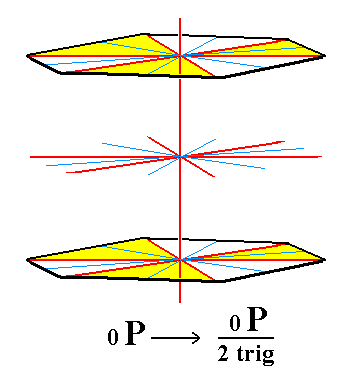 |
Figure 7. The trigonal hemihedric Basic Pinacoid. The colors indicate the mirror symmetries involved. |
This concludes our derivation of all the Forms of the Ditrigonal-bipyramidal Crystal Class by the merohedric approach.
All these Forms can enter in combinations with each other in real crystals.
FACIAL APPROACH
We will now derive those same Forms by subjecting the basic faces (compatible with the Hexagonal Crystal System) one by one to the symmetry operations of the present Class (the Ditrigonal-bipyramidal Crystal Class).
In Part One we found the following seven basic faces compatible with the Hexagonal Crystal System :
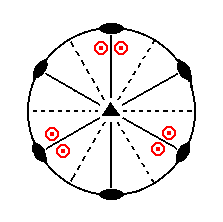 |
Figure 8. Stereogram of the symmetry elements of the Ditrigonal-bipyramidal Crystal Class, and of all the faces of the most general Form. |
The face a : ~a : -a : c generates a trigonal bipyramid when we subject it to the symmetry elements of the present Class. These symmetry elements are listed above. When we subject the face to the 3-fold rotation axis and reflect the result in the equatorial plane of symmetry, we obtain the trigonal bipyramid. The other symmetry elements are then implied.
See Figure 9.
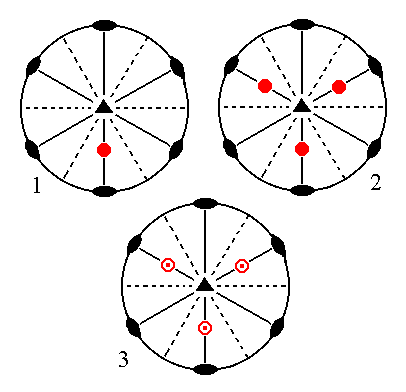 |
Figure 9. (1). Position of the face a : ~a : -a : c in the stereographic projection of the symmetry elements of the Ditrigonal-bipyramidal Crystal Class. (2). Multiplication of the face in virtue of the 3-fold rotation axis. (3). Reflection of the result in the equatorial mirror plane. |
The face 2a : 2a : -a : c generates a type II hexagonal bipyramid when subjected to the symmetry elements of the present Class. First the 3-fold rotation axis generates three faces. These are getting their lower counterparts in virtue of the horizontal mirror plane. The resulting face pairs (each consisting of an upper face and a lower face) are then reflected in the vertical mirror planes (solid straight lines in the stereograms) resulting in the hexagonal bipyramid.
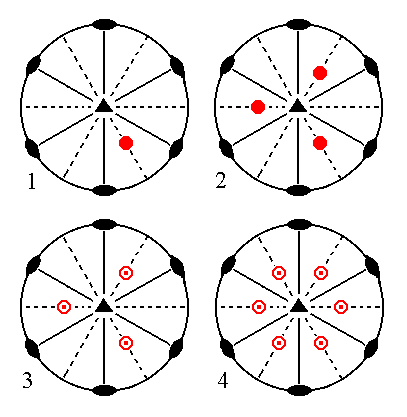 |
Figure 10. (1). Position of the face 2a : 2a : -a : c in the stereographic projection of the symmetry elements of the Ditrigonal-bipyramidal Crystal Class. (2). Multiplication of the face in virtue of the 3-fold rotation axis. (3). Reflection of the result in the equatorial mirror plane. (4). Subjection to the action of the vertical mirror planes. |
The face [3/2]a : 3a : -a : c is a definite face. We will consider its general version, namely the face [s/(s-1)]a : sa : -a : c. When subjected to the symmetry elements of the present Class it will yield a ditrigonal bipyramid. See Figure 11.
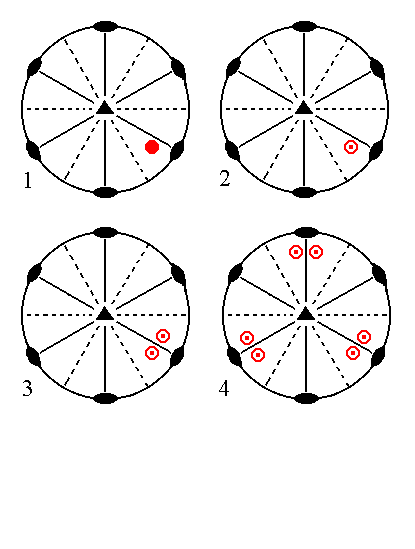 |
Figure 11. (1). Position of the face [s/(s-1)]a : sa : -a : c in the stereographic projection of the symmetry elements of the Ditrigonal-bipyramidal Crystal Class. (2). Reflection of the face in the equatorial mirror plane, resulting in a face pair consisting of an upper face and a lower face. (3). Subjection of this face pair to the action of the nearby vertical mirror plane, resulting in two face pairs. (4). Multiplication of these two face pairs by three in virtue of the 3-fold rotation axis, resulting in the Ditrigonal Bipyramid. |
The face [3/2]a : 3a : -a : ~c is a definite face. Here we will consider its generalized version, namely the face [s/(s-1)]a : sa : -a : ~c. It is vertical. When subjected to the symmetry elements of the present Class it will yield a ditrigonal prism : The nearby vertical mirror plane (solid straight line(s) in the stereogram) will duplicate the face, resulting in a face pair consisting of two vertical faces making an angle (smaller than 1800) with each other. The 3-fold rotation axis will multiply this by three, resulting in three vertical face pairs. Because the faces are vertical the action of the equatorial mirror plane will have no effect, no new faces are generated. The resulting Form is a ditrigonal prism. See Figure 12.
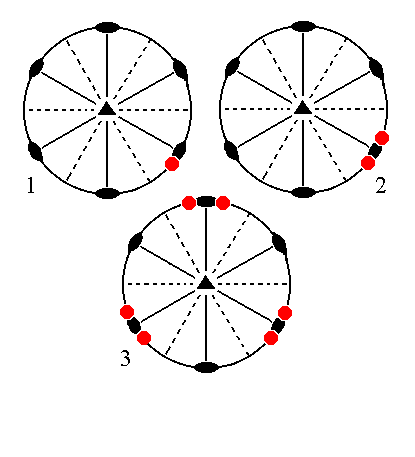 |
Figure 12. (1). Position of the face [s/(s-1)]a : sa : -a : ~c in the stereographic projection of the symmetry elements of the Ditrigonal-bipyramidal Crystal Class. (2). Reflection of the face in a nearby vertical mirror plane, resulting in a face pair consisting of two vertical faces. (3). Multiplication of this face pair by three, in virtue of the 3-fold rotation axis, resulting in the Ditrigonal Prism. |
The face a : ~a : -a : ~c is also a vertical face. When subjected to the symmetry elements of the present Class it will yield a trigonal prism : The nearby vertical mirror plane and 2-fold rotation axis will not have any effect, i.e. they do not generate new faces. So we still have that one face. When this face is subjected to the 3-fold rotation axis we will end up with three vertical faces making up the trigonal prism. The equatorial mirror plane will not add anything new to it because the faces are vertical. Recall that all the prisms are open Forms, so in real crystals they should be closed by other Forms of this Class.
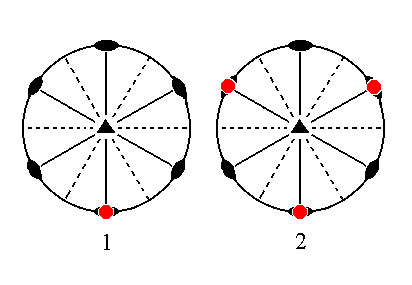 |
Figure 13. (1). Position of the face a : ~a : -a : ~c in the stereographic projection of the symmetry elements of the Ditrigonal-bipyramidal Crystal Class. (2). Multiplication of this face by three, in virtue of the 3-fold rotation axis, resulting in the Trigonal Prism. |
The face 2a : 2a : -a : ~c is also vertical. When we subject it to the symmetry elements of the present Class it will yield a type II hexagonal prism.
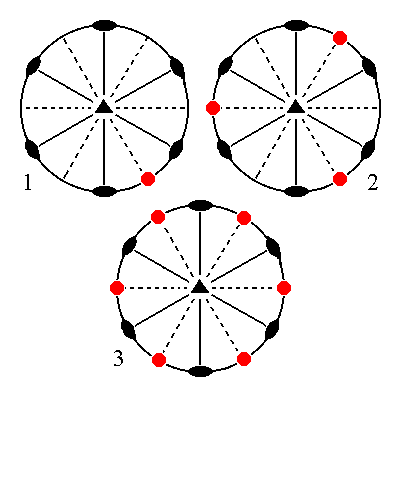 |
Figure 14. (1). Position of the face 2a : 2a : -a : ~c in the stereographic projection of the symmetry elements of the Ditrigonal-bipyramidal Crystal Class. (2). Multiplication of this face by three, in virtue of the 3-fold rotation axis, resulting in three vertical faces. (3). Each face will be duplicated by a nearby vertical mirror plane, resulting in six vertical faces. Because the faces are vertical the equatorial mirror plane will not generate new faces, so the final result is a Hexagonal Prism. |
Finally the face ~a : ~a : ~a : c, which is horizontal, will generate a basic pinacoid -- that is a Form consisting of two horizontal parallel faces -- when we subject it to the symmetry elements of the present Class. The actions of the 3-fold rotation axis and of the vertical mirror planes do not result in new faces, but the equatorial mirror plane will generate a new face parallel to our initial face. The 2-fold rotation axes will not add anything new to the result, so we end up with a Form consisting of two horizontal parallel faces, the basic pinacoid. See Figure 15.
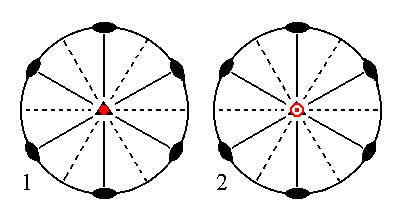
Figure 15.
(1). Position of the face ~a : ~a : ~a : c in the stereographic projection of the symmetry elements of the Ditrigonal-bipyramidal Crystal Class.
(2). Duplication of this face in virtue of the equatorial mirror plane, resulting in two horizontal parallel faces, the Basic Pinacoid.
This concludes our exposition of the Ditrigonal-bipyramidal Crystal Class.
To continue, klick HERE for Part Nine (Class 3 m ).