back to homepage
The External Shapes of periodic 2-D arrays of repeated two-dimensional motifs
Square Net.
We continue our investigation concerning the faces, Forms and combinations of Forms in two-dimensional crystals.
In the previous Part we concluded our investigation concerning the 2-D Rectangular Crystal System. We will now continue our search into 2-D periodic patterns with a discussion of the
2-D Tetragonal Crystal System. This system is based on a square building block and consequently on a square 2-D lattice (net).
The symmetry of its typical square building block (considered as empty) determines the
2-D Tetragonal Crystal System. It has two Classes, 4 and 4mm. From these the Class 4mm can refer to several different Plane Groups, which means that when two 2-D crystals, belonging to the 2-D Tetragonal Crystal System, have the same point symmetry 4mm they can nonetheless differ with respect to their total symmetry content, i.e. they can differ when we also consider their translational symmetries. The reason for this possible difference is a difference in the 'chemical' contents (in our drawings represented by motifs and motif units) of the respective lattices.
A square net (2-D square lattice) is always primitive, which means that there are lattice nodes (nodes are equivalent points) only at the corners of the meshes. When we center such a net then nothing new will be generated. A primitive lattice is denoted by the letter P.
In Figure 1 a possible square net is drawn, and the axial directions are indicated.

Figure 1. A possible square net ( 2-D lattice). This net can accommodate several types of motifs, such that they are periodically repeated across the 2-D plane, according to the geometry of such a net. The axial directions (i.e. crystallographic axes) are indicated. The two axes are perpendicular to each other, and are equivalent. They are chosen to coincide with the relevant edges of the building block (unit mesh).
In constructing 2-D crystal faces we know that only those faces are possible that can be constructed by the periodic stacking of the building blocks (the meshes of the net).
Let us start with the Point Group (= Crystal Class) 4 of this System. The only Plane Group belonging to this Class is the Plane Group P4.
When we introduce a face parallel to one of the crystallographic axes (and consequently perpendicular to the other axis, three new faces are generated in virtue of the 4-fold rotation axis (as the only symmetry element of the Class 4). The result will be a Form consisting of four faces together making up a square, i.e. a closed Form with point symmetry 4. Of course this square does suggest the presence of mirror lines, but the internal structure (i.e. when we furnish the empty building blocks with certain motifs) will forbid this. See Figure 2.
Figure 2. Within the context of Class 4 an introduced initial face implies three more faces, resulting in a Form that has the shape of a square, and a point symmetry 4. The 4-fold rotation axis, perpendicular to the plane of the drawing, is indicated by a small solid blue square. The axial system is indicated (red). The resulting Form is closed, implying that it can as such represent a 2-D Crystal of this Class. See The next Figure.
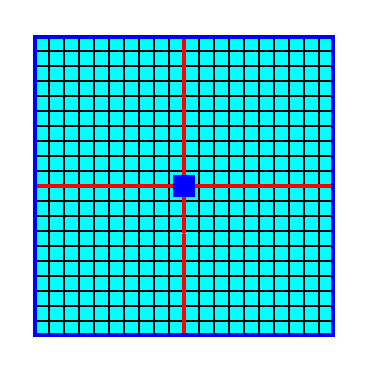
Figure 3. A 2-D crystal of the Class 4 consisting of four faces, together making up one Form. Because we have drawn the crystal such that it consists of empty building blocks, we cannot yet actually see the absence of mirror lines. The finally resulting crystal is depicted in the next Figure.

Figure 3a. A 2-D crystal consisting of the faces defined in the previous two Figures, drawn without axial system and without indication of symmetry elements.
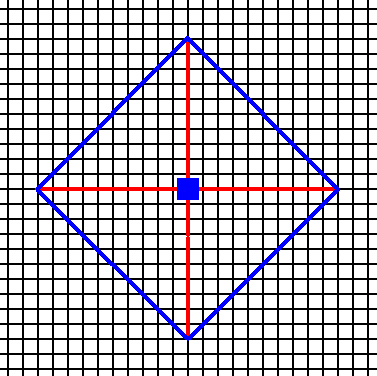
Figure 4. An introduced face making angles of 450 with the crystallographic axes implies three more faces in virtue of the action of the 4-fold rotation axis. The resulting face configuration is again a closed Form that can, on its own behalf, represent a 2-D crystal of the present Class. See the next two Figures.
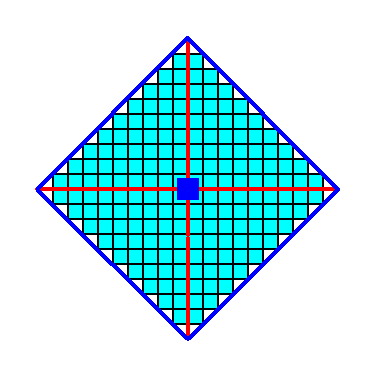
Figure 4a. A two-dimensional crystal, representing the Form of Figure 4. For the final result see the next Figure.

Figure 4b. Final result of the above construction of a 2-D crystal of the Class 4.
Introducing a face with a more general orientation with respect to the system of crystallographic axes gives rise to three more faces in order to make the face configuration obedient to the symmetry content of the present Class. This content is : one 4-fold rotation axis. Again a closed Form is generated, consisting of four faces, and having the shape of a square.
Figure 5. In the context of the symmetry elements of the present Class, namely the presence of a 4-fold rotation axis (indicated by a small solid blue square), an initial face implies three more faces, resulting in a closed Form having the shape of a square. See the next Figure.

Figure 5a. The Form, generated from the above mentioned initial face, is closed and can therefore represent a possible crystal belonging to the present Class (4). See the next Figure.

Figure 5b. A two-dimensional crystal belonging to the Class 4 of the 2-D Tetragonal Crystal System.
The three Forms derived so far all have the same shape, namely that of a square, but their orientations with respect to the axial system differ.
These Forms can enter in combinations with each other, for instance a Form (equivalent to that) of Figure 3a and that of 5b. See Figure 6, 6a, 6b and 6c.
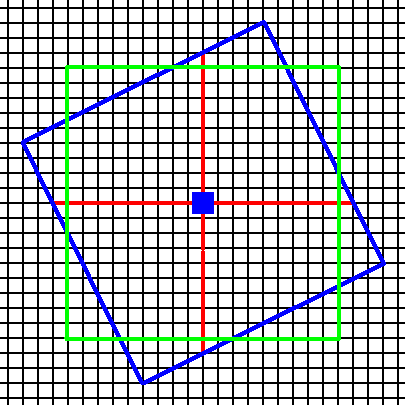
Figure 6. Construction of a combination of two Forms (blue and green) of the Class 4.
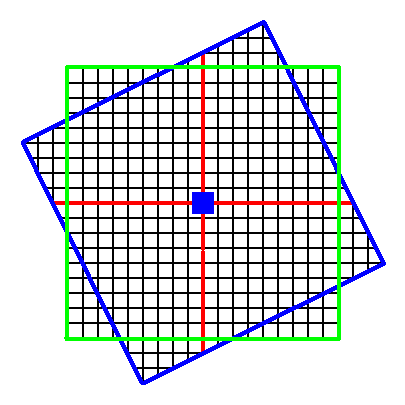
Figure 6a. Continuation of the construction.
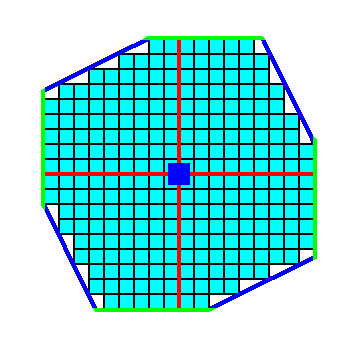
Figure 6b. Removal of indented angles (indented angles will not occur in single crystals). The result is two squares chopping off each other's corners.

Figure 6c. Final result of the construction, representing a 2-D crystal (of the Class 4) consisting of a combination of two Forms.
A combination as the one above can be such that the two Forms balance each other, or that one or the other dominates.
The 'crystals' so far considered are (considered to be) built up by empty building blocks. To conceptually generate genuine (2-D)crystals, those building blocks must be furnished with content, i.e. with motifs (representing chemical units). And indeed, if a certain lattice is given and we insert motifs into it, (motifs) compatible with that lattice (this lattice then describing the specific periodic repeat of those motifs), then the (total) symmetry of the resulting motif pattern is representing a certain Plane Group.
Only one Plane Group belongs to the Class 4 of the 2-D Tetragonal Crystal System. It is the Plane Group P4. Let us display a pattern (given earlier) representing this Plane Group :
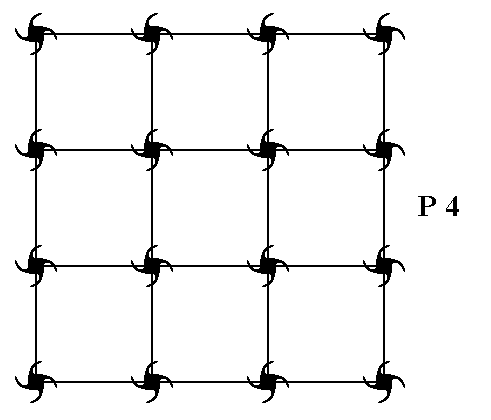
Figure 7. A pattern representing Plane Group P4.
We can now consider the different atomic aspects presented to the environment by the possible faces and Forms of crystals of the Class 4 and representing Plane Group P4 (we will use a square net with smaller meshes than we saw in Figure 7).
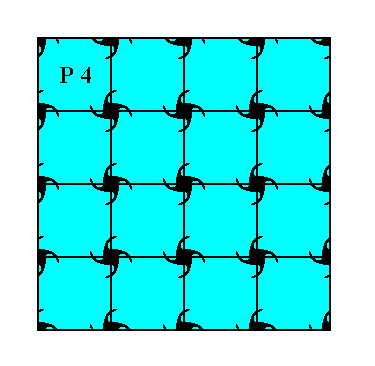
Figure 8. Atomic aspect of the faces -- as derived in the Figures 2, 3 and 3a -- of a 2-D crystal of the Class 4 of the 2-D Tetragonal Crystal System. The incompleteness of motifs at the faces symbolizes unsaturated or distorted chemical valences.
In Figure 8 one can clearly see that the opposite faces of this crystal are not symmetric (with respect to one or another mirror line). The true symmetry of the crystal, namely 4 (and not say 4mm), is revealed by its internal composition, and this composition will reflect itself in certain physical or chemical differences, by means of which one can actually determine that true symmetry (imagining 2-D crystals to exist in reality).
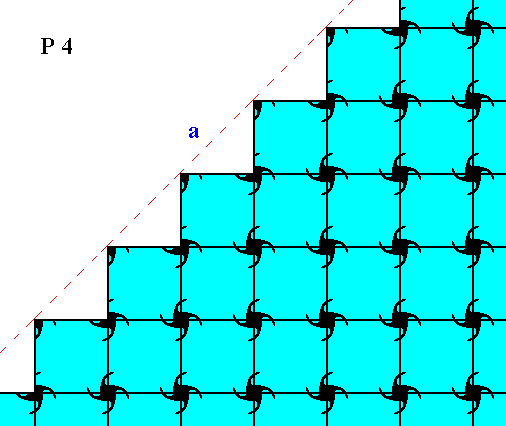
Figure 9. Atomic aspect of one of the faces in the Figures 4, 4a and 4b, here indicated by a .
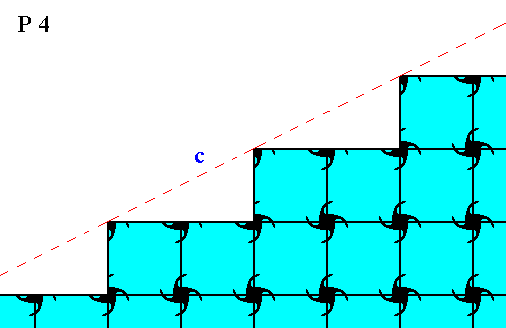
Figure 10. Atomic aspect of one of the faces in the Figures 5, 5a and 5b, here indicated by c .
This concludes our discussion of the Class 4 and its only Plane Group P4.
The second (and last) Crystal Class of the 2-D Tetragonal System is the Class 4mm. It admits of two types of motifs resulting in two different types of periodic pattern according to two different Plane Groups : P4mm and P4gm.
We will derive possible faces, Forms and combinations of Forms within this Class (4mm) :
Figure 11. Introducing a face parallel to one of the crystallographic axes (and consequently perpendicular to the other axis) implies three more faces, resulting in a closed Form having the shape of a square. The four mirror lines do not add more faces beyond these four faces. The symmetry of the resulted face configuration now must be obedient to the symmetry of the Class, 4mm, which means that opposite faces are symmetrical with respect to a horizontal or vertical mirror line, while each two consecutive faces are symmetrical with respect to one or another diagonal mirror line. The 4-fold axis is indicated by a small solid blue square. The crystallographic axes coincide with the non-diagonal mirror lines.
The resulting Form is closed and can as such be a 2-D crystal of our Class :

Figure 11a. This 2-D crystal (Form) of the Class 4mm has the same shape as the corresponding crystal (Form) of the Class 4 (Figure 3a). Their different symmetries cannot be deduced from their external shape. This shape is caused by the internal organization of the crystals. But that same internal organization will also have other effects that reveal the difference in symmetry. Further below, this is illustrated by furnishing the empty building blocks with motifs.
Figure 12. An introduced face, making an angle of 450 with the crystallographic axes, is multiplied by the action of the 4-fold rotation axis, resulting in a closed Form consisting of four faces making up a square. The mirror lines do not add any further faces.
The face configuration so obtained complies with the symmetry of the present Class, 4mm .

Figure 12a. The above Form can represent a 2-D crystal of the Class 4mm . Its external shape is the same as that of the corresponding Form of Class 4 (Figure 4b).
An initial face having a more general orientation with respect to the system of crystallographic axes yields, when subjected to the symmetry elements of the present Class, a Form, so far not yet encountered : a ditetragon. It is a closed Form consisting of eight sides of equal length, but connected to each other by alternating angles, meaning that the ditetragon involves two different angles, four equal angles and four slightly smaller angles, also equal among themselves. See Figures 13, 13a, 13b, 13c and 13d.
Figure 13. A face (blue) with a general orientation with respect to the crystallographic axes is introduced. The resulting face configuration should be such that its symmetry is that of the present Class. This is the same as having that face subjected to the symmetry elements of the present Class. Those symmetry elements are : A horizontal mirror line, a vertical mirror line, two diagonal mirror lines and a 4-fold rotation axis. The next Figures show the action of those symmetry elements upon the introduced face.
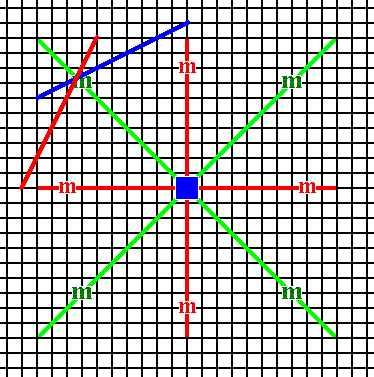
Figure 13a. A second face (red) is generated by the action of one of the diagonal mirror lines.
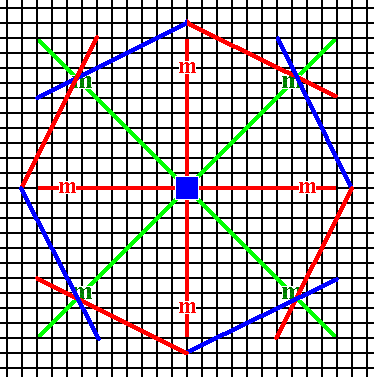
Figure 13b. The face pair of the previous Figure is multiplied four times by the action of the 4-fold rotation axis, resulting in eight faces making up a ditetragon, i.e. an octagon consisting of eight equal faces connected by alternating angles.
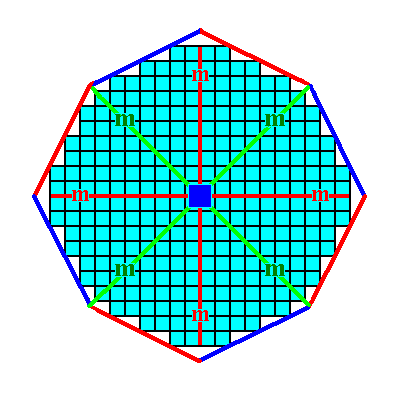
Figure 13c. The ditetragon is a closed Form and can represent a crystal of the present Class. See Figure 13d.

Figure 13d. A 2-D crystal representing the above derived Form. It belongs to the Class 4mm of the 2-D Tetragonal Crystal System.
These Forms can enter in combinations with each other.
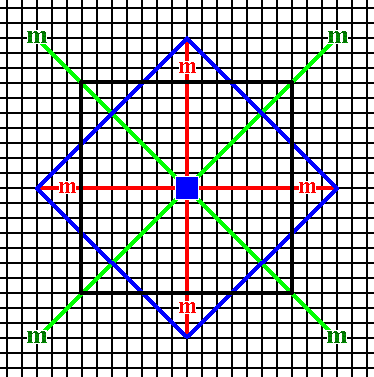
Figure 14. A combination of two Forms (specified above) of the 2-D Crystal Class 4mm. The relative growth rates of the (faces of the) involved Forms determine the prominence of either the one Form or the other. A combination like this one can represent a 2-D crystal (See Figures 14a and 14b).
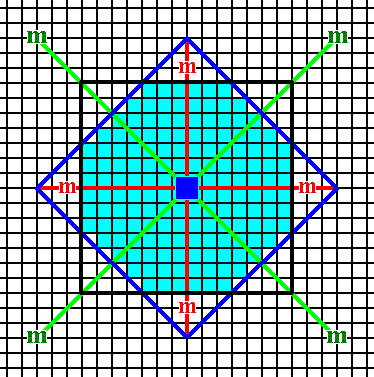
Figure 14a. Outlining the 2-D crystal (light blue) consisting of two Forms as described above (See also next Figure).

Figure 14b. A two-dimensional crystal of the Class 4mm consisting of two Forms of that Class, as specified above.
As has been said, this Class is compatible with two Plane Groups, namely P4mm and P4gm. We're going to investigate the possible different atomic aspects presented by the above derived faces and Forms of our Class 4mm. These aspects can be considered when the empty building blocks are furnished with motifs, leading to the two possible Plane Groups.
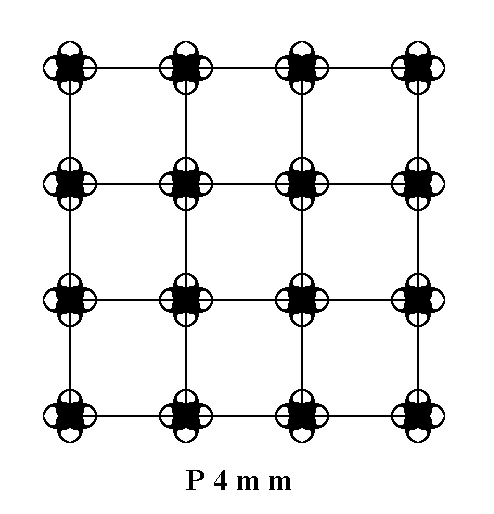
Figure 15. A periodic pattern of motifs representing Plane Group P4mm.
We can now consider the different atomic aspects presented to the environment by the possible faces and Forms of crystals of the Class 4mm and representing Plane Group P4mm (we will use a square net with smaller meshes than we saw in Figure 15).
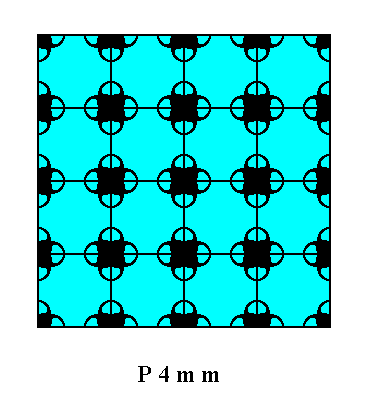
Figure 16. Atomic aspects presented to the environment of the faces (as derived in Figure 11, and 11a) of a crystal belonging to the Class 4mm and to the Plane Group P4mm. The incompleteness of motifs at the faces express the presence of unsatisfied or distorted chemical valences.
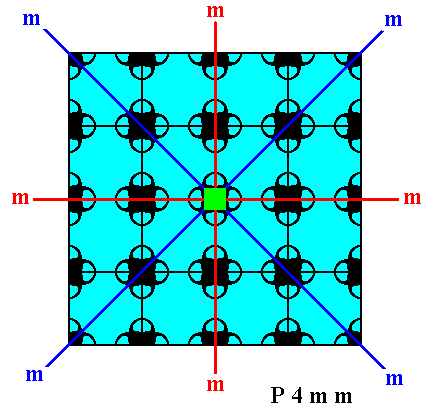
Figure 16a. Indication of the point symmetry of the crystal of Figure 16.
Red and blue lines : The two types of mirror lines. The red lines are at the same time the two crystallographic axes. The small solid green square indicates the 4-fold rotation axis.
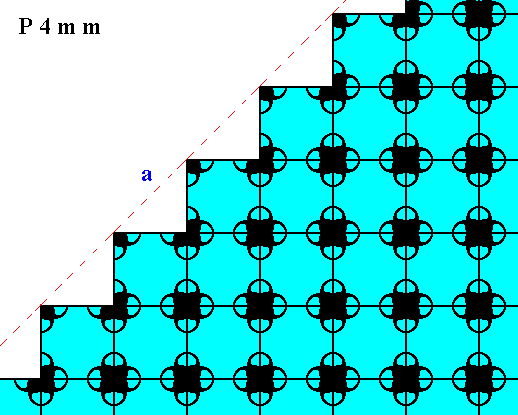
Figure 17. Atomic aspect of one of the faces of the Figures 12, and 12a, here indicated by a .
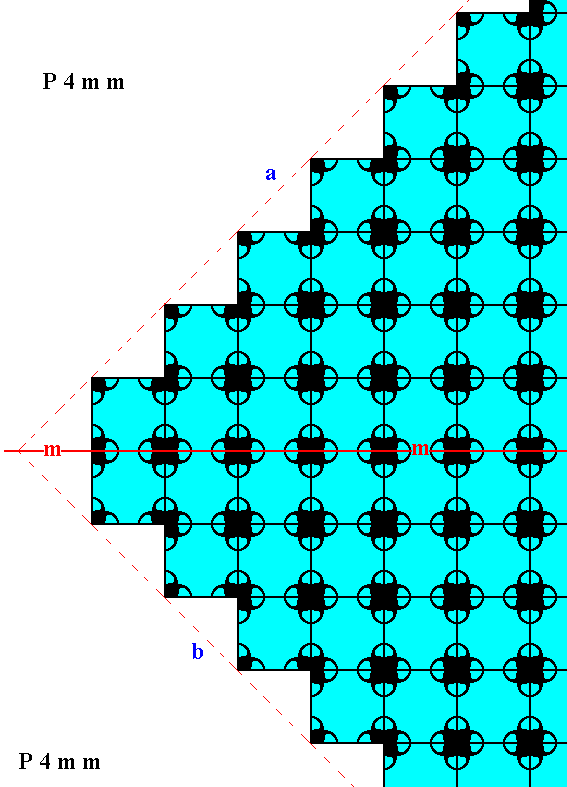
Figure 17a. Atomic aspects of two consecutive faces of the Figures 12, and 12a, here indicated by a and b. The mirror symmetry of those two faces with respect to the indicated (red) mirror line (m) -- a symmetry demanded by the point symmetry of the crystal to which this fragment belongs -- is clearly evident from the pattern.
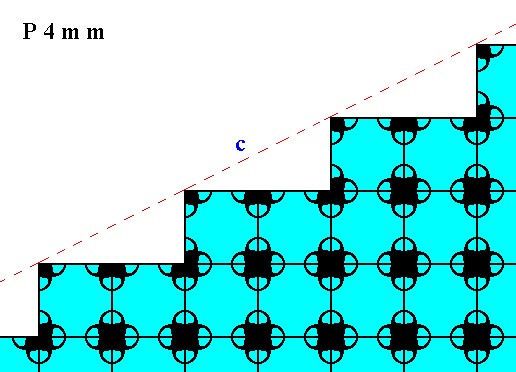
Figure 18. Atomic aspect of the face of Figure 13, here indicated by c.
The second (and last) Plane Group of the Class 4mm is the Plane Group P4gm. We will discuss it in the next Part.
To continue, click HERE for Part Fourteen.
back to homepage