back to homepage
The External Shapes of periodic 2-D arrays of repeated two-dimensional motifs
Square Net. (continued)
We continue our investigation concerning the faces, Forms and combinations of Forms in two-dimensional crystals.
In the previous Part we established possible faces, Forms and combinations of Forms within the 2-D Tetragonal Crystal System, based on the Square Net with respect to its empty building blocks.
We considered the Class 4 and its only Plane Group P4. Then we went on to consider the Class 4mm, and discussed the first of its Plane Groups, P4mm. Here we will continue with the Class's second and last Plane Group P4gm.
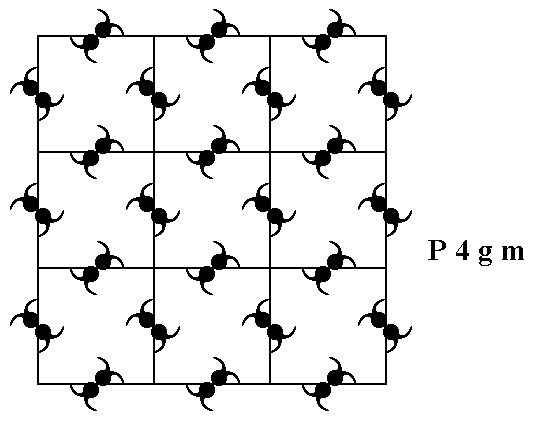
To do so, let us first reproduce a pattern representing this Plane Group.

Figure 1. A periodic motif pattern representing Plane Group P4gm.
We will now present the atomic aspects presented to the environment by possible faces of 2-D crystals of the Class 4mm and representing the Plane Group P4gm.
Figure 2. Atomic aspects presented to the environment by the faces as derived in the Figures 11 and 11a of Part Thirteen.
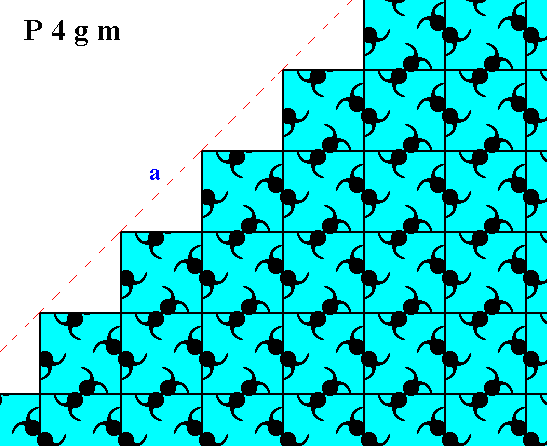
Figure 3. Atomic aspect presented to the environment by one of the faces of the Figures 12 and 12a in Part Thirteen, here indicated by a .
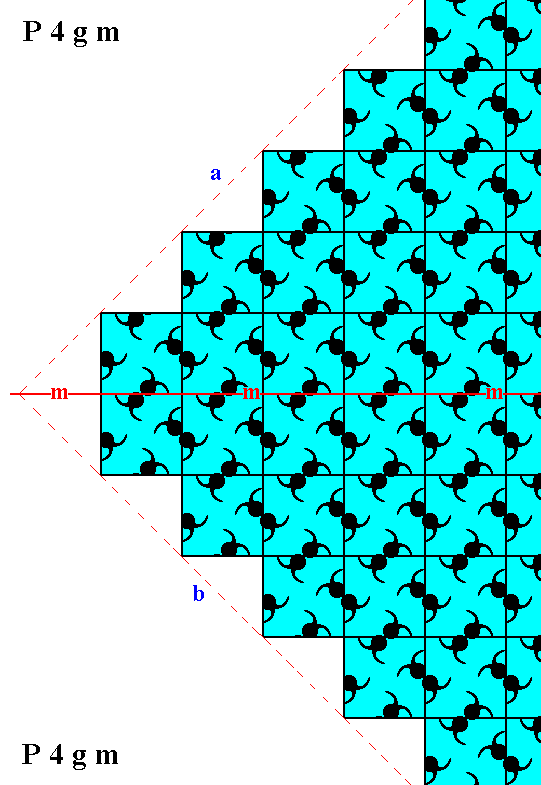
Figure 4. Atomic aspects of two consecutive faces of the Figures 12 and 12a in Part Thirteen, here indicated by a and b. One of the point symmetry elements, namely the horizontal mirror line (m) is indicated. As is visible in the Figure the internal organization is not symmetric with respect to this mirror line.
Because -- as we will show -- the cause of the asymmetry with respect to a horizontal mirror line situated between the two faces a and b as observed above, is just a small diagonal shift according to half the diagonal of a unit mesh, this asymmetry is macroscopically not visible. The shift is according to glide translations inherent in the total symmetry of the pattern. See for these glide translations Figure 5.

Figure 5. The symmetry of a pattern representing Plane Group P4gm contains three types of glide lines : horizontal, vertical and diagonal. The diagonal glide line type -- only one individuals diagonal glide line is depicted here -- implies a glide translation vector that has the same direction as the sum vector of the horizontal and vertical translation vectors.
In the next two Figures we depict respectively one of the vertical, and one of the horizontal glide lines and indicate the glide translation vector involved.
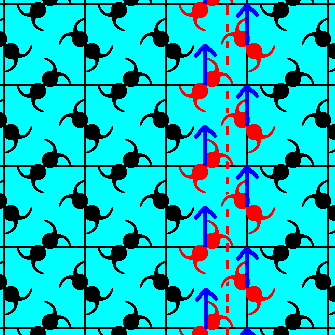
Figure 6. The glide translation vector (blue arrows) associated with a vertical glide line, present in a pattern representing Plane Group P4gm. Each glide line operation (as the one depicted here) consists of two components : a translation (according to the glide translation vector) + mirror operation. The mentioned translation lies along the glide line, while the mirror operation is a reflection with respect to that same glide line.
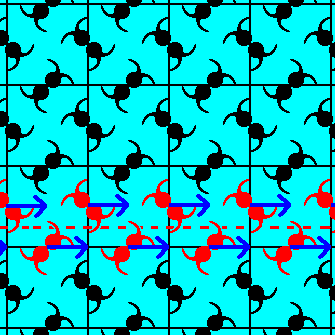
Figure 7. The glide translation vector (blue arrows) associated with a horizontal glide line, present in a pattern representing Plane Group P4gm.
When we subject the pattern (thought as being indefinitely extended) to such a glide line operation, the pattern will be mapped onto itself.
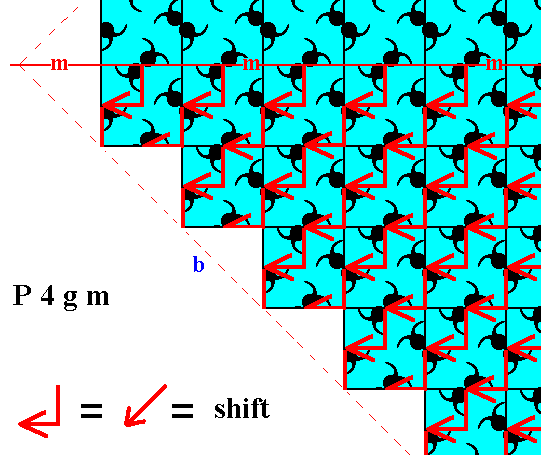
Figure 8. A shift of the lower half of the pattern of Figure 4, in virtue of a diagonal vector, indicated by its two components (a horizontal an a vertical component), effects the whole pattern, i.e. lower plus upper half, to be mirror symmetrical with respect to the horizontal mirror line (m) as one of the point symmetry elements. See the next Figure.
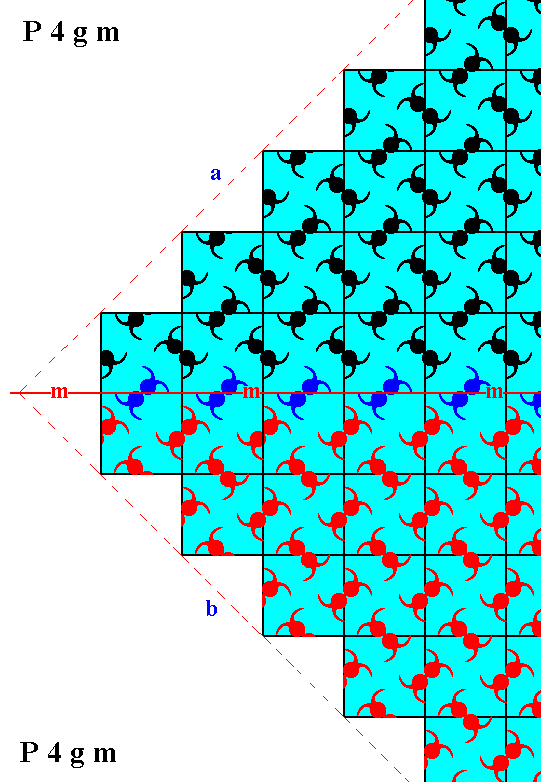
Figure 9. According to Figure 8 we shift the motifs as indicated in that figure. The shifted motifs are shown in red. But the motifs, lying on the horizontal mirror line (m), and indicated in blue, are, it is true, also shifted, but a copy of them remains at the original locations. So they are not themselves results of any shift. The faces a and b are symmetrical, and now also according to the internal structure, except for one row of motifs (indicated in blue), lying on the mirror line itself. Such a discrepancy of just one row is, however, macroscopically invisible.
The next Figure depicts the 2-D crystal of Figure 2, and shows that a mirror symmetry with respect to a vertical mirror line, and as such macroscopically expressed by the symmetry of the faces d and e (supposing that the depicted crystal is extended to macroscopical dimensions), is not supported by the internal organization.
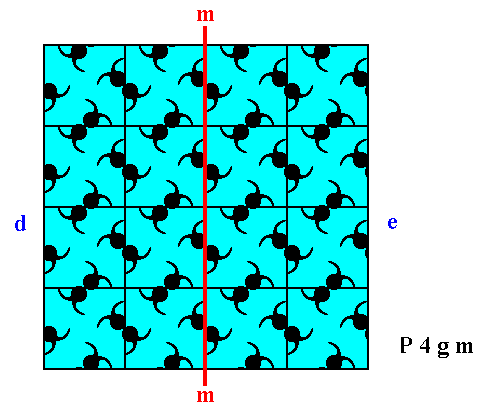
Figure 10. A two-dimensional crystal of the Class 4mm, and belonging to the Plane Group P4gm.
A vertical mirror line (m), representing one of its point symmetry elements, is indicated. This point symmetry (macroscopically expressed by the faces d and e being symmetric) is not supported by the internal structure.
Restoration of the symmetry with respect to that vertical mirror line (as demanded by the present Class) can be accomplished by the translation vector indicated in the next Figure.

Figure 11. A translation vector, shifting a motif pattern over a microscopical distance, can be used to restore mirror symmetry, i.e. to show that the asymmetry is just caused by such a translation.
If we shift the right hand half of the pattern represented by the crystal of Figure 10 according to the above vector, then the mirror symmetry with respect to the indicated vertical mirror line is restored, i.e. the internal structure now complies with this symmetry, except for one row of motifs (indicated in blue). Because the length of the vector involved is microscopically small, the (macroscopical) crystal will not show the asymmetry. It will display complete symmetry with respect to the indicated vertical mirror line. See the next Figure.
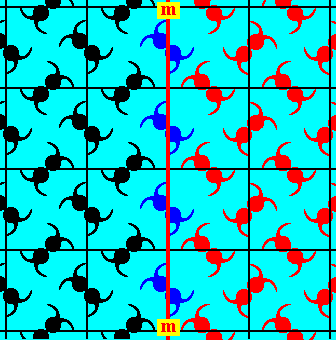
Figure 12. The right hand half of the pattern representing Plane Group P4gm differs from the left hand part by a shift of the motifs according to the vector indicated in Figure 11. In virtue of this shift the mirror symmetry with respect to the indicated vertical mirror line (m) is restored, as such revealing the cause of the asymmetry.
The next Figure is about the diagonal mirror lines as demanded by the point symmetry of the present Class.
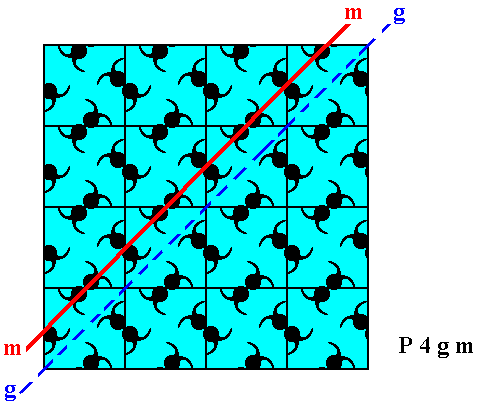
Figure 13. The internal structure of a pattern representing Plane Group P4gm possesses (only) diagonal mirror lines. One of them is indicated (m) in the Figure. These diagonally oriented mirror lines do not go through the centers of the relevant meshes. Although there is consequently no such mirror line present at the location indicated by the dashed blue line (g), which actually is just a glide line, it takes only a shift of 1/4 of the diagonal of the unit mesh to posit such a mirror line at that location. Because the mentioned shift is microscopically small we will not detect the absence of a mirror line at the location mentioned, i.e. we will see the presence of a diagonal mirror line going right through the center of the crystal. The same applies for the line perpendicular to that line and also going through that center.
The next Figure gives just another atomic aspect presented to the environent by a possible crystal face of the present Class.
Figure 14. Atomic aspect presented to the environment by a possible face (derived in Figure 13 in Part Thirteen) of a 2-D crystal belonging to Class 4mm and representing Plane Group P4gm.
We now have discussed all the Plane Groups and the associated atomic aspects presented to the environment by possible crystal faces, and with it we have considered exhaustively the 2-D Tetragonal Crystal System.
In the next Part we will discuss the possible faces, Forms, combinations of Forms and atomic aspects relating to the 2-D Hexagonal Crystal System.
To continue, click HERE for Part Fifteen.
back to homepage