
back to homepage
The External Shapes of periodic 2-D arrays of repeated two-dimensional motifs
We continue our investigation concerning the faces, Forms and combinations of Forms in two-dimensional crystals.
In the previous Part we concluded our investigation of possible faces, Forms, combinations of Forms and the associated atomic aspects within the 2-D Tetragonal Crystal System, based on the Square Net. Now we will consider the 2-D Hexagonal Crystal System.
Hexagonal Net.
On this net the 2-D Hexagonal Crystal System is based. A regular hexagon can be considered as the empty building block of the crystals belonging to his System. It has four Classes (Point groups), 3, 3m, 6 and 6mm. The Class 3 can be represented by one Plane Group, the Class 3m by two, the Class 6 by one, and the Class 6mm also by one. All crystals of the 2-D Hexagonal Crystal System are based on a primitive (hexagonal) net.
In the Figures 1 and 2 a possible hexagonal net is drawn, and the axial system is indicated. This axial system consists of three equivalent crystallographic axes making angles of 600 with each other.
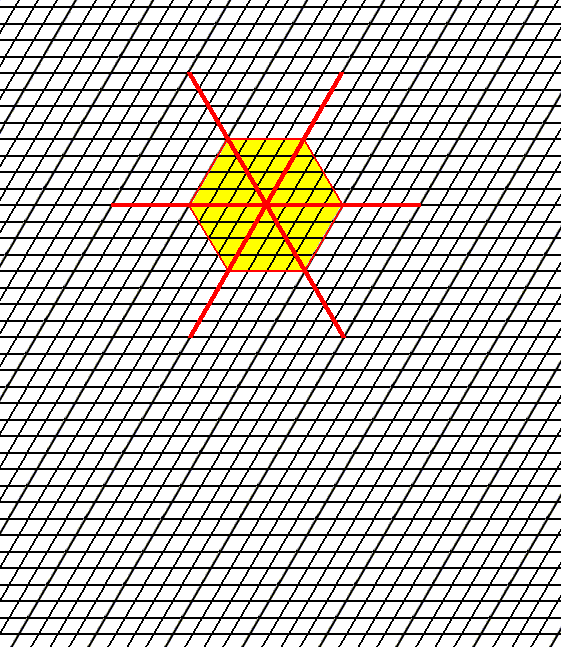
Figure 1. A possible hexagonal net, forming the basis of the structure of 2-D crystals belonging to the 2-D Hexagonal Crystal System. A hexagon is marked (yellow) in order to better visualize the axial system.

Figure 2. The hexagonal net with the axial system. This system consists of three equivalent axes making angles of 600 with each other.
In constructing 2-D crystal faces we know that only those faces are possible that can be constructed by the periodic stacking of the building blocks (the meshes of the net).
Let us start with the Class (Point Group) 3. Crystals belonging to this Class exhibit a point symmetry 3 which means that macroscopically the only symmetry element they possess is a 3-fold rotation axis.
When we introduce a face parallel to one of the crystallographic axes, it will be multiplied by three in virtue of the 3-fold rotation axis. The result is an equilateral triangle. Geometrically this triangle possesses mirror lines, but crystallographically it does not possess any mirror line.
See Figure 3.
Figure 3. An introduced initial face, parallel to one of the crystallographic axes, implies
two more faces, together making up a triangle (trigon). It is a closed Form and can represent a crystal of this Class (See the next Figure).
The 3-fold rotation axis is indicated by the blue solid triangle. It is perpendicular to the plane of the drawing.

Figure 4. A two-dimensional crystal of the Class 3 of the 2-D Hexagonal System.
If we introduce a face perpendicular to one of the crystallographic axes, then two more faces are generated in virtue of the action of the 3-fold rotation axis. The result is again an equilateral triangle, but having a different orientation from that of the above derived Triangle.
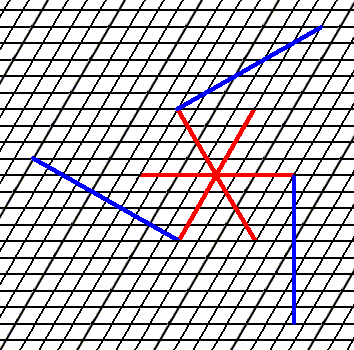
Figure 5. An initial face implies two more faces in order for the resulting Form to be consistent with the point symmetry of the present Class (3). Because crystallographically only the orientations of the faces matters, the faces can be extended till they meet resulting in a triangle, which is a closed Form and thus can represent a 2-D crystal (See the next Figures).
The 3-fold rotation axis is situated in the center of the axial system.
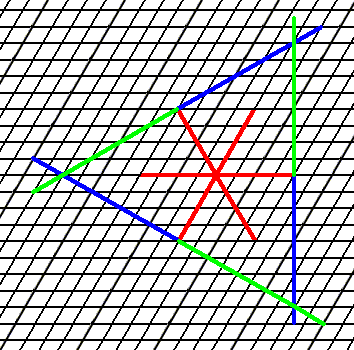
Figure 6. Extension of the faces of Figure 5 yields a triangle.
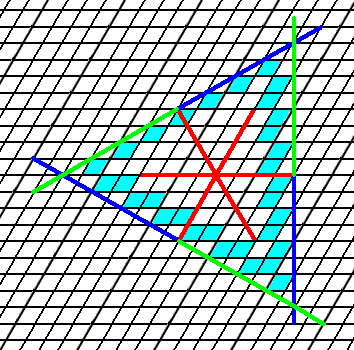
Figure 7. As Figure 6, but with outline of crystal indicated.

Figure 8. A two-dimensional crystal of the Class 3, representing the above derived Form.
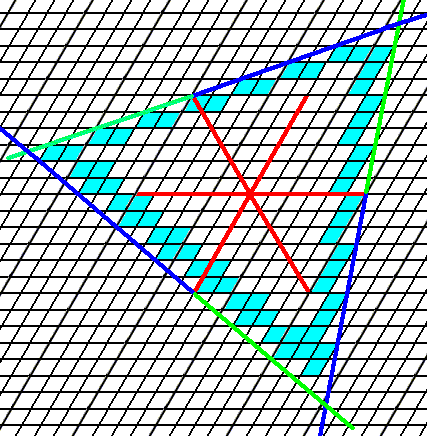
Figure 9. When we introduce a face with a more general orientation (See upper face in Figure), two more faces are implied by the symmetry (3) of the present Class, resulting (after extension) in a closed Form, having the shape of an equilateral triangle. The outline of a crystal, representing this Form, is given.

Figure 10. A two-dimensional crystal of the Class 3 of the 2-D Hexagonal Crystal System, representing the above derived Form.
An introduced face with yet another general orientation with respect to the crystallographic axes is multiplied by the 3-fold rotation axis resulting again in a closed Form having the shape of an equilateral triangle. See the next Figure.
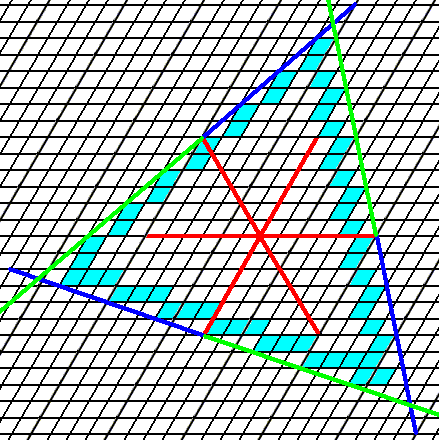
Figure 11. (Yet another) initial face implies two more faces yielding a Form having a point symmetry consistent with that of the present Class (3). The Form again has the shape of an equilateral triangle and can represent a crystal of this Class (See next Figure).

Figure 12. A two-dimensional Crystal of the Class 3 of the 2-D Hexagonal Crystal System, as a result of the above construction.
These Forms not only can, each for themselves, represent crystals of the Class 3, but also combinations of them can represent crystals of this same Class.
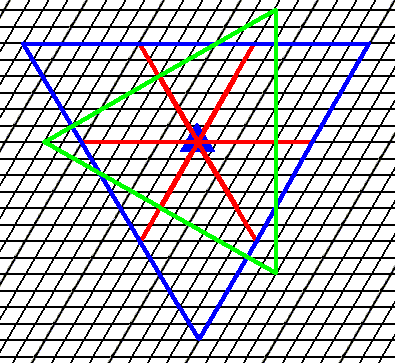
Figure 13. Combining the Forms of the Figures 3 (blue) and 6 (green) results in a new crystal, indicated in the next Figure.
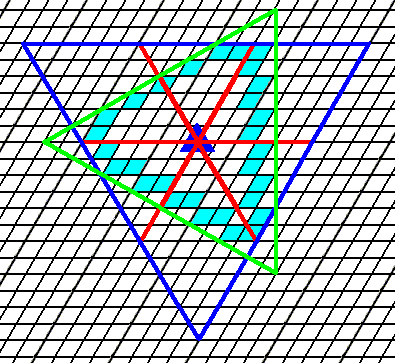
Figure 14. The outline of the crystal, consisting of the two mentioned Forms, is indicated. The next Figure depicts the whole crystal.

Figure 15. A two-dimensional crystal of the Class 3 of the 2-D Hexagonal Crystal System. It is a combination of two Forms as specified above.
The present Class, 3, admits of one Plane Group only, namely P3.
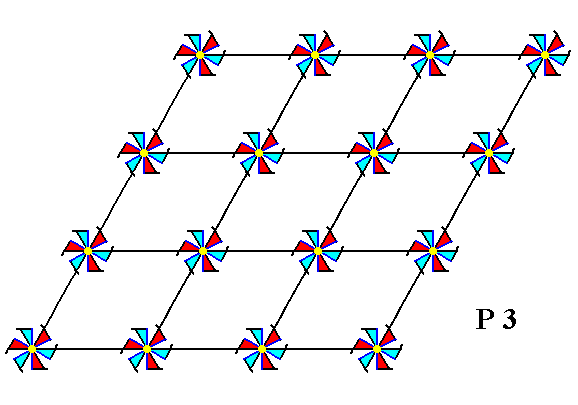
Figure 16. A pattern of repeated motifs (as given earlier), representing Plane Group P3.
The point symmetry of each motif is 3 (indicated by their shape and coloration), which means that the only symmetry element that such a motif possesses is a 3-fold rotation axis.
The next Figure is a pattern equivalent to the one in the previous Figure, but based on a net with smaller meshes. We will use this for the exposition of the possible atomic aspects.

Figure 17. A pattern of repeated motifs -- the same motifs as in Figure 16 -- representing Plane Group P3, now based on a net with smaller meshes than the one used in Figure 16 (coloration of motifs slightly changed for convenience).
The next Figure shows the atomic aspects presented to the environment by the faces of Figures 3 and 4.
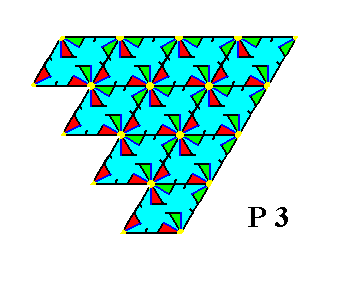
Figure 18. Atomic aspects presented to the environment by some possible faces (together making up a possible Form) of the Class 3 of the 2-D Hexagonal Crystal System.
In the next Figure the net (which is only a device to describe the ordering of the motifs, and as such just a device to guide the inspecting eye) is removed. Only the motif pattern as such is preserved.
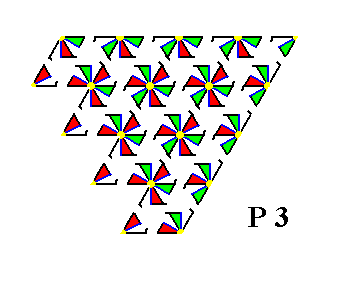
Figure 19. A pattern of repeated motifs delimited by the three faces as derived in the Figures 3 and 4, representing Plane Group P3. The hexagonal net is omitted.
In the above Figure something strange can be observed : At the faces we see incomplete motifs. Earlier we established that these must be interpreted as unsatisfied chemical valences or distorted valences (i.e. distorted bonds).
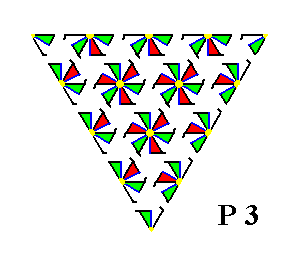
Figure 20. The pattern of the above Figures, now delimited correctly, is fully consistent with the symmetry of the present Class, which consists in possessing 3-fold rotational point symmetry. The 3-fold rotation axis of the triangular pattern is shown in the next Figure.
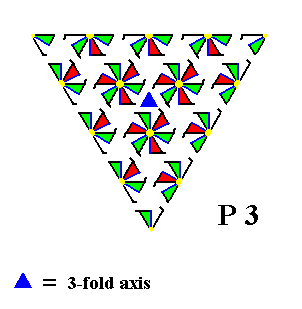
Figure 21. The 3-fold rotation axis of the triangular pattern of Figure 20 is indicated. This means that when the structure is rotated by 360/3 = 1200 it will map onto itself, not only with respect to its external shape but also with respect to its internal structure. Of course a crystal of this kind is supposed to consist of millions and millions of such motifs arranged according to the present Figure. So from a microscopic standpoint the number of these repeating motifs can be considered to be essentially infinite. And this implies that in fact every rotation of 1200 about any point that is equivalent to the location of the 3-fold axis as indicated in the Figure, will map the structure onto itself. The particular 3-fold rotation axis indicated in the Figure represents the point symmetry of the crystal.
As can be seen in the Figure there are no mirror lines present. So the whole structure complies with the point symmetry of the present Class, which is the Class 3.
Maybe another choice of building block yields directly the correct results. These could be hexagonal building blocks instead of rhombic building blocks.

Figure 22. The hexagonal net is supplemented with diagonal lines, causing the plane to be tiled by equilateral triangles. Six such triangles make up a hexagon, that, consequently, can also tile the plane, and thus can serve as a building block for the structure. See the next Figure.

Figure 23. The same as the previous Figure. One hexagonal building block is indicated.
Four such hexagonal building blocks can build a triangular crystal with the same orientation as the one indicated in Figure 3. See the next Figure.

Figure 24. Indication of a triangular 2-D crystal having the same orientation as the one indicated in Figure 3, and built up by four hexagonal building blocks. One can eaily see that the triangular structure complies fully with the point symmetry of the present Class.
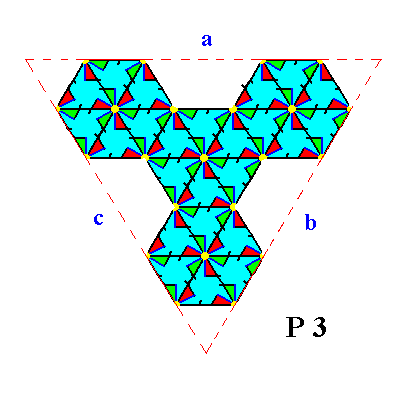
Figure 25. Result of the construction of the 2-D crystal, specified above. It is a crystal belonging to Class 3, and with it to Plane Group P3, of the 2-D Hexagonal Crystal System. The three faces are indicated by a, b and c. The incomplete motifs indicate unsatisfied or distorted chemical valences. As has been said, such a crystal should consist of millions of building blocks, effecting the faces of the crystal to be smooth macroscopically.
In the next Part we will elaborate further on the faces, Forms and atomic aspects belonging to the present crystal Class.
To continue, click HERE for Part Sixteen.
back to homepage