The Hexagonal Crystal System (Part Eleven)
back to homepage

back to Part One
back to Part Two
back to Part Three
back to Part Four
back to Part Five
back to Part Six
back to Part Seven
back to Part Eight
back to Part Nine
back to Part Ten

The Trigonal-pyramidal Class
(= Hemimorphy of Trigonal Tetartohedric)   3

This Class can be derived from the Forms of the Trigonal Tetartohedric Division (= Trigonal-bipyramidal Class) by applying hemimorphy to those Forms. Hemimorphy is a special kind of hemihedric and consists of suppressing the main mirror plane, here the equatorial mirror plane. So these Forms are ultimately derived from the holohedric Forms by first applying trigonal hemihedric (Described in Part Eight) and then, to the result, pyramidal hemihedric (Described in Part Three, and then to that result in turn yet another hemihedric, which in this case is a hemimorphy. Such a three-fold application of hemihedrics is called an ogdohedric. The present derivation means that in the Forms of the Trigonal Tetartohedric Division we suppress the horizontal mirror plane. With respect to the trigonal tetartohedric Forms we end up with independent halves of their bipyramids, called monopyramids, further, independent halves of the basic pinacoid, called pedia (monohedra). The prisms retain their shape but their symmetry will be lowered accordingly (which here means that their main axis becomes polar). The symmetry elements of this Class are :

Derivation of the Forms of the Trigonal-pyramidal Class
(= hemimorphy of Trigonal Tetartohedric)

MEROHEDRIC APPROACH.
The Forms of this Class will be found when we subject the Forms of the Trigonal Tetartohedric Division to hemimorphy, which means that we suppress their horizontal mirror plane.
Recall from Part Ten that the Forms of the Trigonal-bipyramidal Crystal Class (= Trigonal Tetartohedric Division) were the following :

Trigonal Tetartohedric Type I Trigonal Bipyramid
Trigonal Tetartohedric Type II Trigonal Bipyramid
Trigonal Tetartohedric Type III Trigonal Bipyramid
Trigonal Tetartohedric Type I Trigonal Prism
Trigonal Tetartohedric Type II Trigonal Prism
Trigonal Tetartohedric Type III Trigonal Prism
Trigonal Tetartohedric Basic Pinacoid

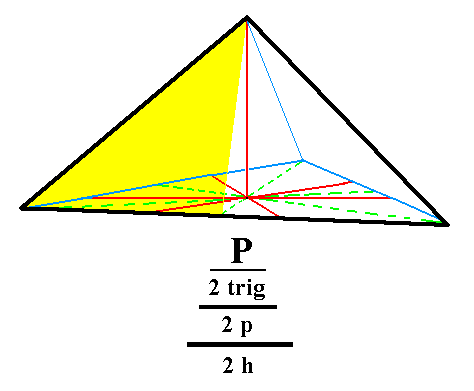
From the trigonal tetartohedric type I trigonal bipyramid we can derive the ogdohedric trigonal monopyramid by subjecting it to hemimorphy. Two such monopyramids are possible, an upper one and a lower one. See Figure 1.

Figure 1. An ogdohedric Type I Trigonal Monopyramid. The partial coloring expresses the absence of the mirror plane perpendicular to the (partially colored) face. The same applies to the other two faces. This Form -- like all the Forms of this Class -- does not possess any mirror plane whatsoever. It is moreover an open Form consisting only of three faces. The straight lower boundaries should not suggest the presence of a base face. Such a base face can only be present at the pyramid in the form of a combination of the present Form with a pedion. The same considerations apply to all the monopyramids that will follow. Of course also the prisms (to be considered further below) are open Forms, and also the pedion (also to be considered below).
The subsymbol "2 h" in the Naumannsymbol means that hemimorphy is being applied (to a trigonal tetartohedric Form).
See for the corresponding trigonal tetartohedric Form (from which the present Form is derived by hemimorphy), Figure 1 of Part Ten.
From the trigonal tetartohedric type II trigonal bipyramid (Figure 2c, Part Ten) can be derived the ogdohedric type II trigonal monopyramid by applying hemimorphy. Also here two such monopyramids are possible, an upper and a lower one. One is depicted in Figure 2.

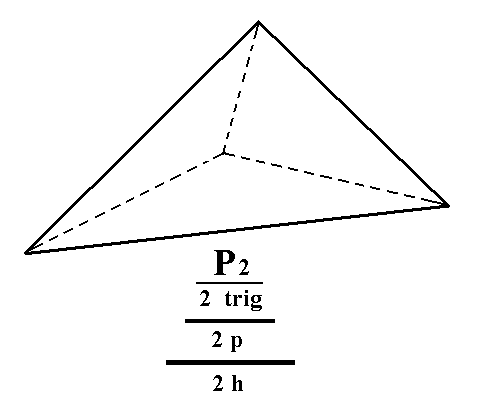
Figure 2. An ogdohedric Type II Trigonal Monopyramid. It is just the upper half of the trigonal tetartohedric Type II Trigonal Bipyramid. The lower half is yet another independent Form.
From the trigonal tetartohedric type III Trigonal Bipyramid (Figure 3c, Part Ten) can be derived the ogdohedric type III trigonal monopyramid by applying hemimorphy.
See Figure 3.

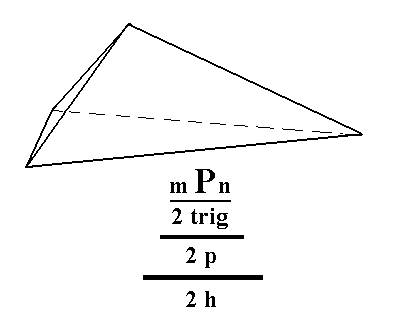  Figure 3. An ogdohedric Type III Trigonal Monopyramid. It is just the upper half of the trigonal tetartohedric Type III Trigonal Bipyramid. The lower half is yet another independent Form.
From the trigonal tetartohedric type I trigonal prism we can derive the ogdohedric type I trigonal prism by applying hemimorphy. See Figure 4.

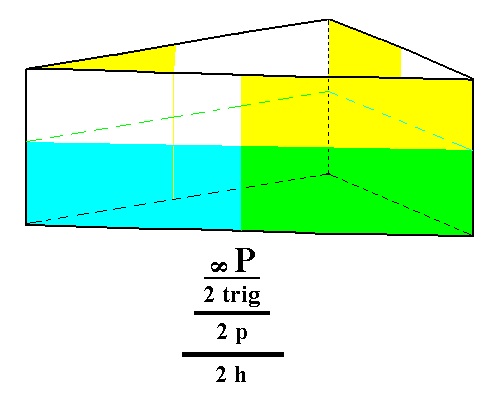
Figure 4. An ogdohedric Type I Trigonal Prism. The application of hemimorphy is indicated by means of the coloring of the front face :   It is devided in two sections, an upper and lower one, expressing the suppression of the equatorial mirror plane. This suppression does not however entail the face's disappearance. The same goes for the other two faces, so the external shape is not affected by hemimorphy.
From the trigonal tetartohedric type II trigonal prism we can derive the ogdohedric type II trigonal prism by applying hemimorphy. See Figure 5.

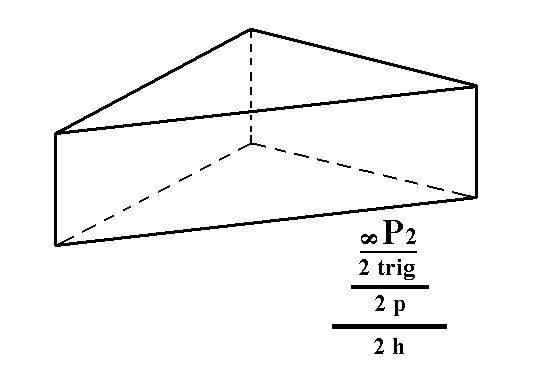
Figure 5. An ogdohedric Type II Trigonal Prism. Like the type I prism the hemimorphy does not effect a different shape, but the symmetry content is lowered accordingly.
From the trigonal tetartohedric type III trigonal prism we can derive the ogdohedric type III trigonal prism, by applying hemimorphy. See Figure 6.

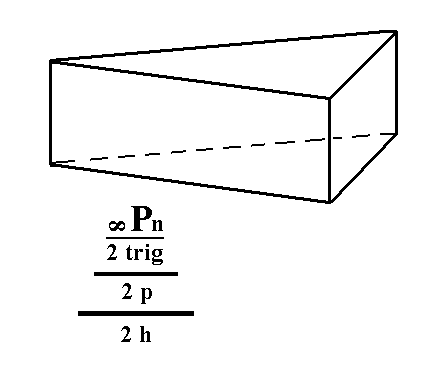
Figure 6. An ogdohedric Type III Trigonal Prism. Also in this case hemimorphy does not affect the external shape but lowers the symmetry content accordingly.
From the trigonal tetartohedric basic pinacoid (Figure 7a, Part Ten) we can derive the ogdohedric pedion when applying hemimorphy. In this case the trigonal tetartohedric basic pinacoid, which consists of two horizontal parallel faces, loses its equatorial mirror plane, resulting in two independent pedions. A pedion is one (horizontal) face. Like the prisms, the basic pinacoid (not belonging to this Crystal Class) and the monopyramids, it is an open Form. See Figure 7.

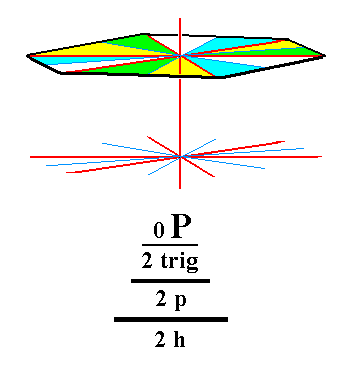  Figure 7. An ogdohedric Pedion, derived by hemimorphy from the trigonal tetartohedric Basic Pinacoid. Two such pedions are possible, an upper one (as depicted here) and a lower one, independent of each other.
This concludes our derivation of all the Forms of the Trigonal-pyramidal Crystal Class, by means of the merohedric approach.
All these Forms can enter (in the present case SHOULD enter) in combinations with each other in real crystals.
FACIAL APPROACH

We will now derive those same Forms by subjecting the basic faces (compatible with the Hexagonal Crystal System) one by one to the symmetry operations of the present Class (the Trigonal-pyramidal Crystal Class).
In Part One we found the following seven basic faces compatible with the Hexagonal Crystal System :

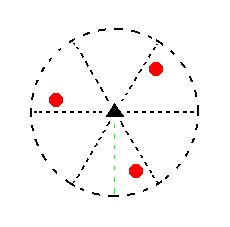The stereographic projection of the symmetry elements of this Class is given in Figure 8.

  Figure 8. Stereogram of the symmetry elements of the Trigonal-pyramidal Crystal Class, and of all the faces of the most general Form.
The face a : ~a : -a : c generates an ogdohedric type I trigonal monopyramid when subjected to the symmetry elements of the present Class. The only symmetry element of this class is a 3-fold rotation axis coincident with the vertical crystallographic axis (the c axis). This 3-fold rotation axis triples the face, resulting in a trigonal monopyramid. See Figure 9.

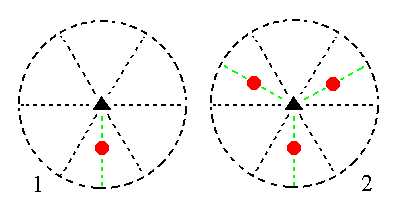  Figure 9.
(1). Position of the face a : ~a : -a : c in the stereogram of the symmetry elements of the Trigonal-pyramidal Crystal Class.
(2). Tripling of the face in virtue of the 3-fold rotation axis, resulting in a trigonal monopyramid.
The face 2a : 2a : -a : c generates an ogdohedric type II trigonal monopyramid when subjected to the symmetry elements of the present Class. The 3-fold rotation axis (as the only symmetry element of the Class) triples the face, resulting in a trigonal monopyramid.
See Figure 10.

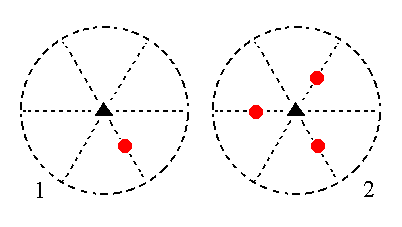  Figure 10.
(1). Position of the face 2a : 2a : -a : c in the stereogram of the symmetry elements of the Trigonal-pyramidal Crystal Class.
(2). Tripling of the face in virtue of the 3-fold rotation axis, resulting in a trigonal monopyramid.
The face [3/2]a : 3a : -a : c is a definite face. Here we will consider a generalized version of it, namely the face [s/(s-1)]a : sa : -a : c. It will generate an ogdohedric type III trigonal monopyramid when subjected to the 3-fold rotation axis. The latter will triple the face resulting in a trigonal monopyramid. See Figure 11.

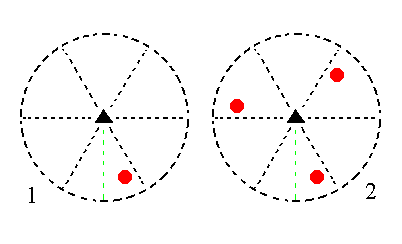  Figure 11.
(1). Position of the face [s/(s-1)]a : sa : -a : c in the stereogram of the symmetry elements of the Trigonal-pyramidal Crystal Class.
(2). Tripling of the face in virtue of the 3-fold rotation axis, resulting in a trigonal monopyramid.
The face [3/2]a : 3a : -a : ~c is a definite face. Here we will consider the generalized version of it, namely the face [s/(s-1)]a : sa : -a : ~c. It is vertical. It generates an ogdohedric type III trigonal prism when subjected to the 3-fold rotation axis :   This axis generates a total of three vertical faces making up a trigonal prism. See Figure 12.

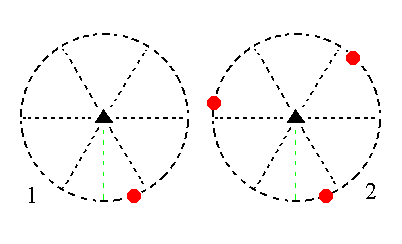  Figure 12.
(1). Position of the face [s/(s-1)]a : sa : -a : ~c in the stereogram of the symmetry elements of the Trigonal-pyramidal Crystal Class.
(2). Tripling of the face in virtue of the 3-fold rotation axis, resulting in a trigonal prism.
The face a : ~a : -a : ~c is also vertical. It generates an ogdohedric type I trigonal prism when subjected to the 3-fold rotation axis :   It will be tripled, resulting in three vertical faces making up a trigonal prism. See Figure 13.

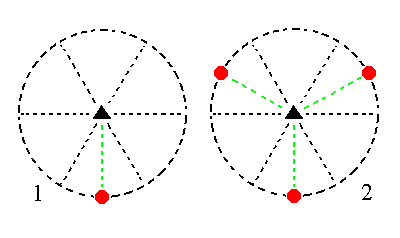  Figure 13.
(1). Position of the face a : ~a : -a : ~c in the stereogram of the symmetry elements of the Trigonal-pyramidal Crystal Class.
(2). Tripling of the face in virtue of the 3-fold rotation axis, resulting in a trigonal prism.
The face 2a : 2a : -a : ~c is also vertical. It generates an ogdohedric type II trigonal prism when subjected to the 3-fold rotation axis :   This axis triples the face resulting in three vertical faces making up a trigonal prism. See figure 14.

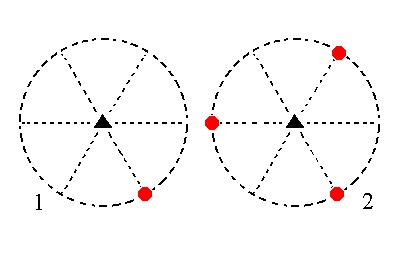  Figure 14.
(1). Position of the face 2a : 2a : -a : ~c in the stereogram of the symmetry elements of the Trigonal-pyramidal Crystal Class.
(2). Tripling of the face in virtue of the 3-fold rotation axis, resulting in a trigonal prism.
The face ~a : ~a : ~a : c, finally, is horizontal. It generates an ogdohedric pedion (monohedron) when subjected to the 3-fold rotation axis. This axis does not generate new faces in this case, so the result is one horizontal face, the pedion. See Figure 15.

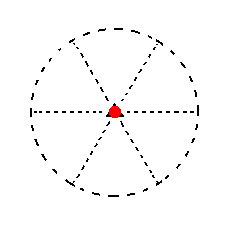  Figure 15.
Position of the face ~a : ~a : ~a : c in the stereogram of the symmetry elements of the Trigonal-pyramidal Crystal Class.
The action of the symmetry elements of this Class, i.e. of the 3-fold rotation axis, does not generate new faces, so the resulting Form is just this one (horizontal) face, a Pedion.
This concludes our exposition of the Trigonal-pyramidal Crystal Class.
To continue, klick HERE for Part Twelve (Class 3 2 ).

back to homepage

back to Part One

back to Part Two

back to Part Three

back to Part Four

back to Part Five

back to Part Six

back to Part Seven

back to Part Eight

back to Part Nine

back to Part Ten

****************