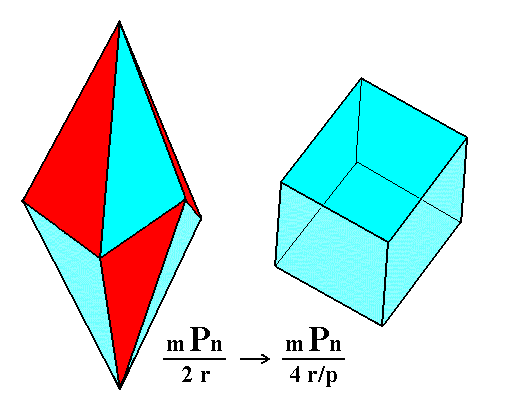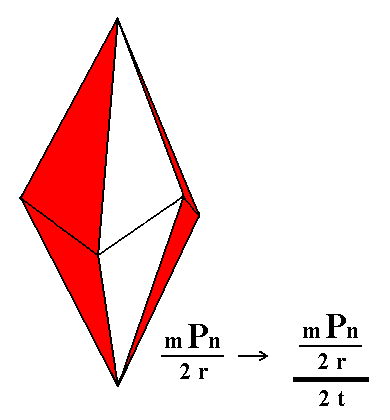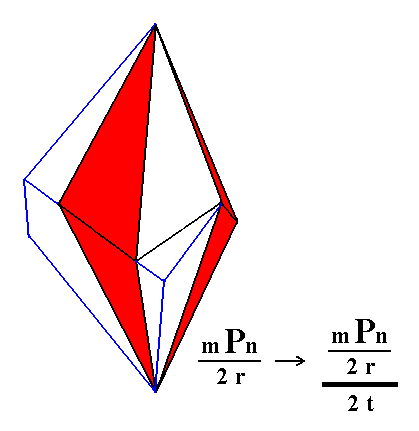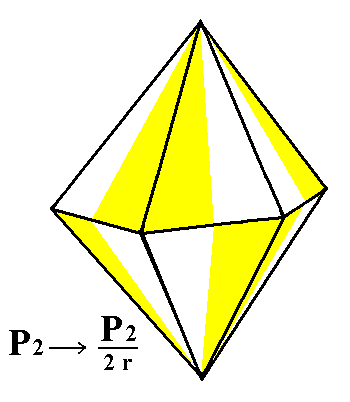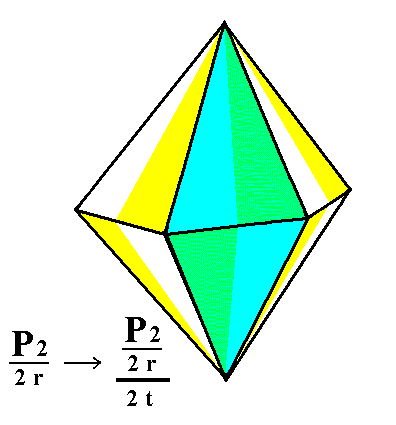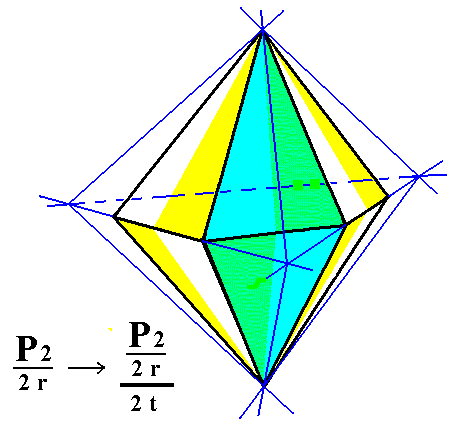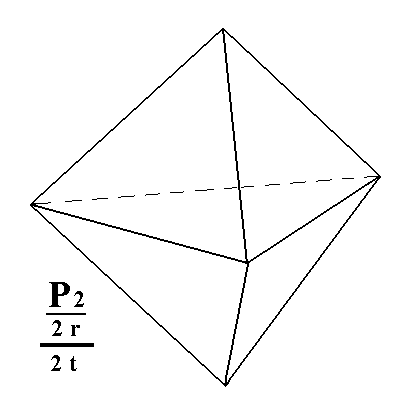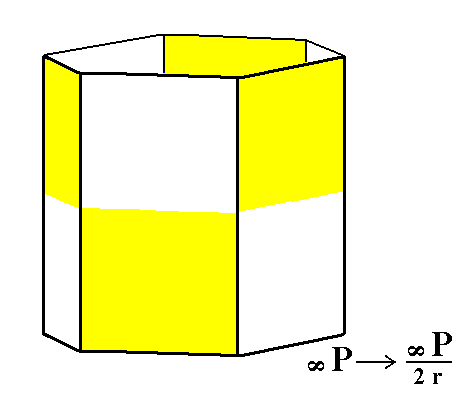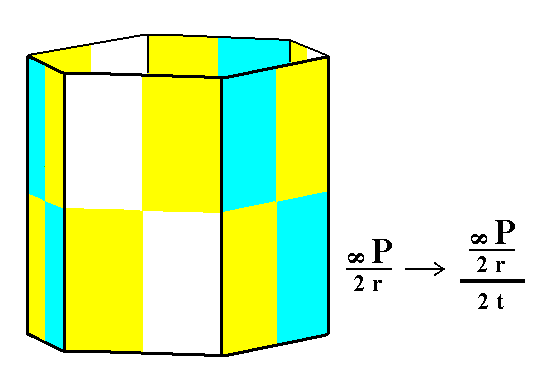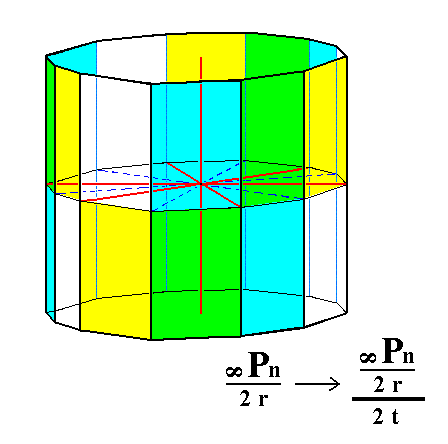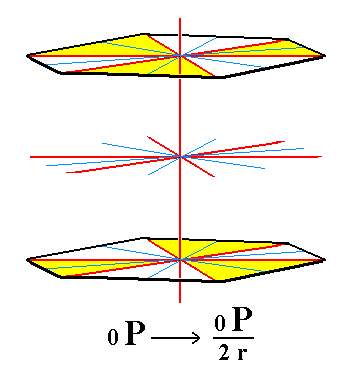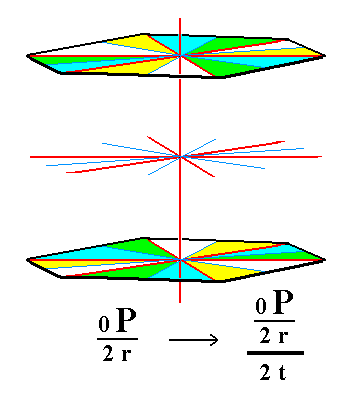back to homepage
back to Part One
back to Part Two
back to Part Three
back to Part Four
back to Part Five
back to Part Six
back to Part Seven
back to Part Eight
back to Part Nine
back to Part Ten
back to Part Eleven
Rhombohedron
Rhombohedric Hemihedric Type II Hexagonal Bipyramid
Ditrigonal Scalenohedron
Rhombohedric Hemihedric Type I Hexagonal Prism
Rhombohedric Hemihedric Type II Hexagonal Prism
Rhombohedric Hemihedric Dihexagonal Prism
Rhombohedric Hemihedric Basic Pinacoid
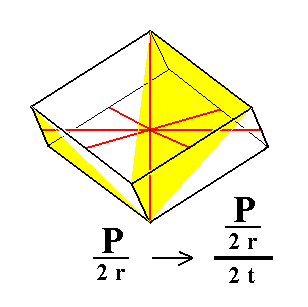
From the rhombohedron we can derive the trapezohedric tetartohedric rhombohedron when trapezohedric hemihedric is applied to it, which -- as has been said -- means that all mirror planes are suppressed. The external shape will not undergo any change, but the symmetry content is lowered accordingly. See Figure 1.
 |
Figure 1. The trapezohedric tetartohedric Rhombohedron, derived from the (rhombohedric hemihedric) Rhombohedron. The sign "2 r" in the Naumann symbol means the application of rhombohedric hemihedric, while the sign "2 t" stands for the application of trapezohedric hemihedric. The partition of the faces (to express the suppression of mirror planes) is shown for the three front faces only. |
In Part Seven we expounded the Trigonal-rhombohedric Class (= Rhombohedric Tetartohedric Division). In deriving the Forms of this Trigonal-rhombohedric Class we wrote :
"This Class can be derived from the Rhombohedric Hemihedric Class (Division) (= the Ditrigonal-scalenohedric Class) by applying pyramidal hemihedric to its Forms. This means that in the Forms of the Rhombohedric Hemihedric Division we suppress all six vertical mirror planes. "
In the present Class -- The Trigonal-trapezohedric Class
(= Trapezohedric Tetartohedric Division) -- we seem to do the same : In the Forms of the Rhombohedric Hemihedric Division we suppress all renaining mirror planes.
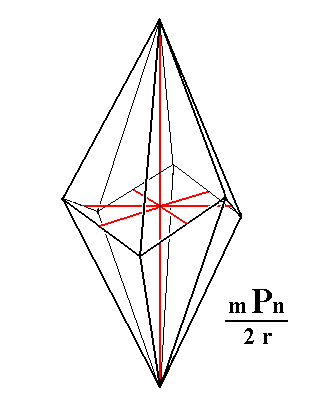
One such rhombohedric hemihedric Form is the ditrigonal scalenohedron, that we depict here once more (Figure 1a) :
 |
Figure 1a. A Ditrigonal Scalenohedron, and its orientation with respect to the four crystallographic axes. |
In Part Seven (concerning the Rhombohedric Tetartohedric Division) we derived from this scalenohedron a tetartohedric Form -- a rhombohedron -- by suppressing all remaining mirror planes of this scalenohedron :
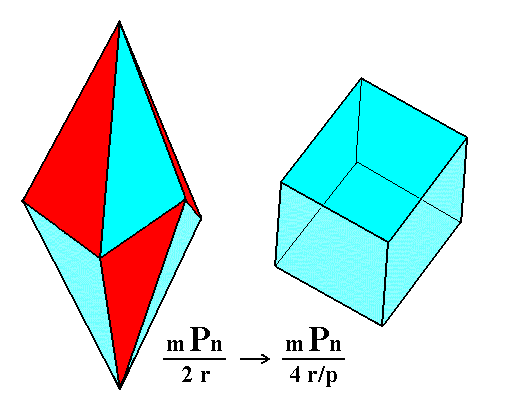
Figure 1b. Derivation of a Type III Rhombohedron from (the blue faces of) a Ditrigonal Scalenohedron.
Only the shapes of the respective Forms (Scalenohedron, Rhombohedron) are given. They are not necessarily drawn at precisely the same scale.
Here we see in what way we express the suppression of mirror planes by means of the alternate coloring of faces, of which either the red or the blue faces are suppressed and the others allowed to extend till they meet. In the above Figure we chose the blue faces to make up the resulting rhombohedron.
Well there is yet another way to suppress the remaining mirror planes which is indicated in the next Figure :
 |
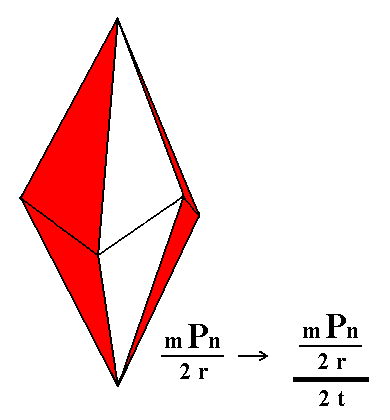Figure 1c. Another possible partition of a Ditrigonal Scalenohedron, representing trapezohedric hemihedric. |
 |
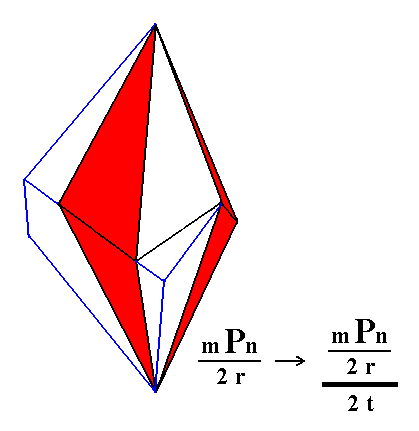Figure 1d. Construction of a Trigonal Trapezohedron from the red faces of the partition in Figure 1c. |
 |
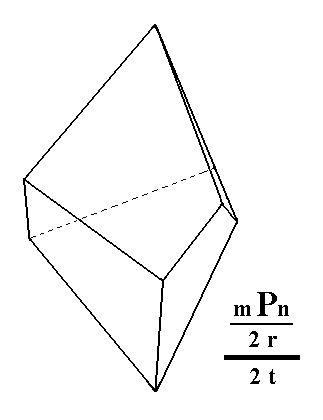Figure 1e. Result of the construction of a Trigonal Trapezohedron from the red faces of the partition in Figure 1c. A similar, but enantiomorphous (i.e. mirror image), Trigonal Trapezohedron can be derived from the white faces in Figure 1c. |
So we now have derived from the ditrigonal scalenohedron the (trapezohedric tetartohedric) trigonal trapezohedron, and have at the same time shown how to partition a rhombohedric hemihedric Form to obtain a trapezohedric tetartohedric Form. This same type of partition we applied in the case of the rhombohedron above (Figure 1, the partition is shown there for the three front faces only).
From the rhombohedric hemihedric type II hexagonal bipyramid (Figure 2) we can derive the trapezohedric tetartohedric trigonal bipyramid. Two such trigonal bipyramids are possible, as shown in Figure 2a.
 |
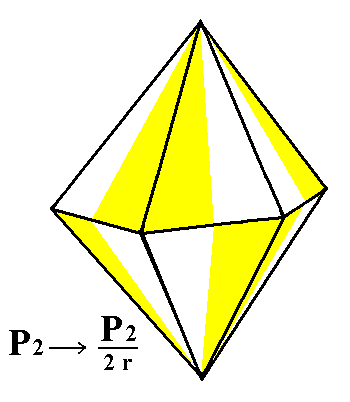Figure 2. The holohedric Deuteropyramid retains its external shape when subjected to rhombohedric hemihedric. From this resulting rhombohedric hemihedric Type II Hexagonal Bipyramid two trapezohedric tetartohedric Trigonal Bipyramids can be derived. See Figure 2a. |
 |
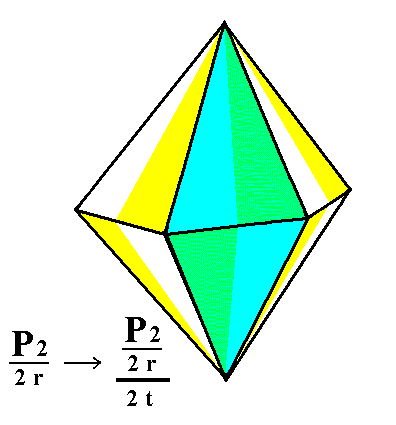Figure 2a. Partition of the rhombohedric hemihedric Type II Hexagonal Bipyramid. This partition involves two face categories : (1) green-blue, and (2) yellow-white. Two trigonal bipyramids can be derived depending on which face category is suppressed --expressing the dropping of mirror planes -- while the faces of the other category are allowed to extend till they meet. |
 |
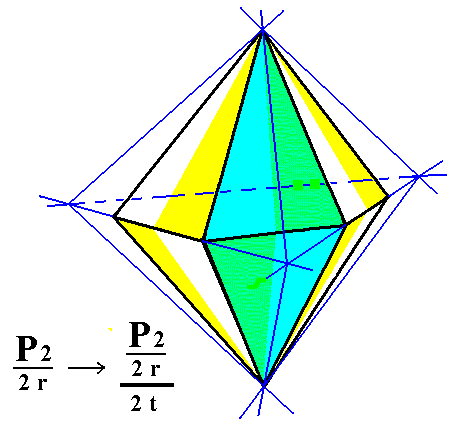Figure 2b. Construction of a Trigonal Bipyramid, from the yellow-white faces. |
 |
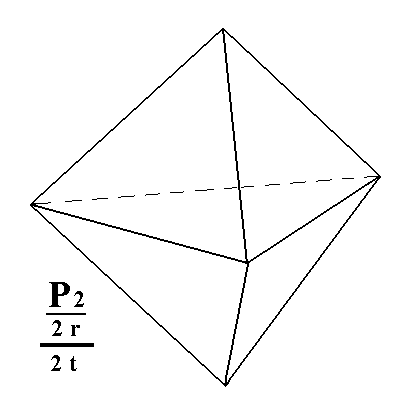Figure 2c. Result of the construction of a Trigonal Bipyramid, from the yellow-white faces. |
From the rhombohedric hemihedric type I hexagonal prism we can derive the trapezohedric tetartohedric type I hexagonal prism. See Figures 3 and 3a.
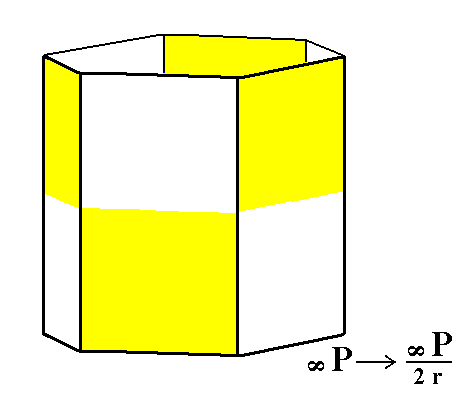
Figure 3. The holohedric Protoprism does not alter its shape when subjected to rhombohedric hemihedric, but loses some symmetry. From this rhombohedric hemihedric prism can be derived the trapezohedric tetartohedric Type I Hexagonal Prism (See Figure 3a).
No change in external shape is involved.
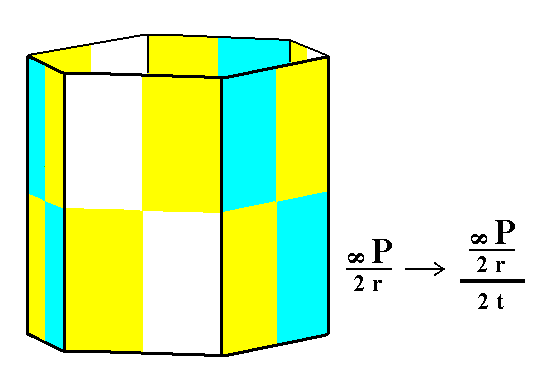
Figure 3a. The trapezohedric tetartohedric Type I Hexagonal Prism.
The coloring symbolizes the absence of mirror planes, and also the presence, not of a 6-fold rotation axis, but a 3-fold rotation axis.
From the rhombohedric hemihedric type II hexagonal prism we can derive the trapezohedric tetartohedric trigonal prism.
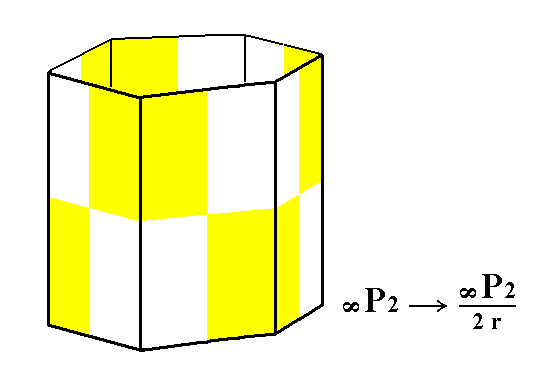
Figure 4. The holohedric Deuteroprism does not alter its shape when subjected to rhombohedric hemihedric, but loses some symmetry. From this rhombohedric hemihedric Type II Hexagonal Prism will be derived the trapezohedric tetartohedric Trigonal Prism (See Figure 4a).
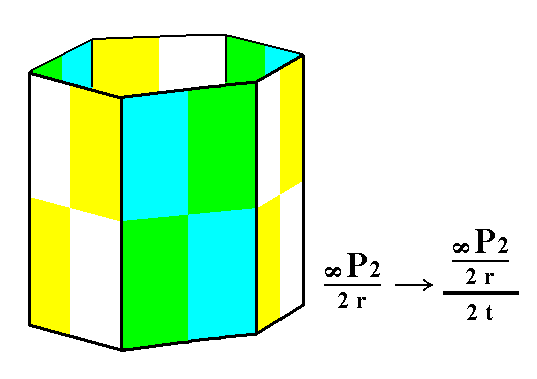
Figure 4a. Partition of the rhombohedric hemihedric Type II Hexagonal Prism in two face categories : (1) green-blue, and (2) yellow-white. Suppressing one category and allowing to extend the (faces of the) other category will yield a trapezohedric tetartohedric Trigonal Prism. One such prism is constructed in the next Figure.
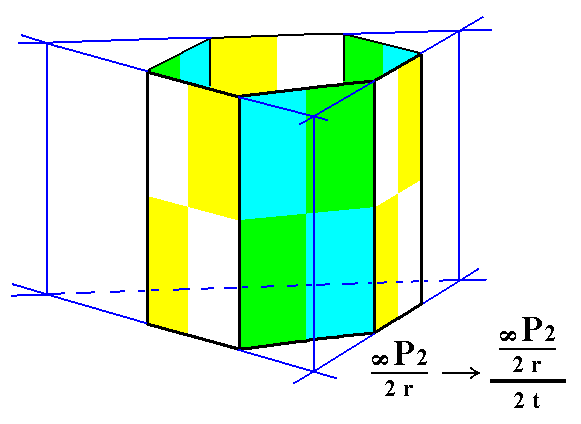
Figure 4b. Construction of a trapezohedric tetartohedric Trigonal Prism, from a rhombohedric hemihedric Type II Hexagonal Prism by extention of the yellow-white faces and suppression of the green-blue faces.
The result of this construction is shown in Figure 4c.
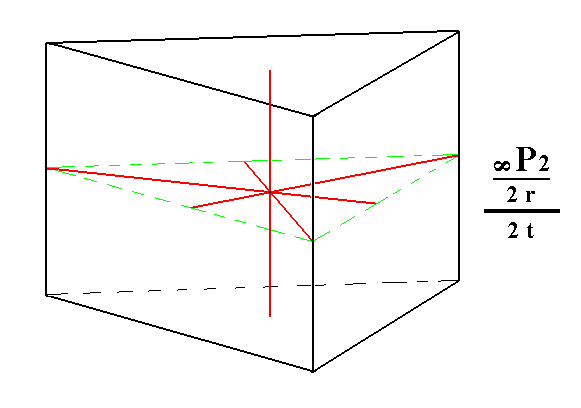
Figure 4c. Result of the construction of a trapezohedric tetartohedric Trigonal Prism.
From the rhombohedric hemihedric dihexagonal prism we can derive the trapezohedric tetartohedric ditrigonal prism, See Figure 5.
 |
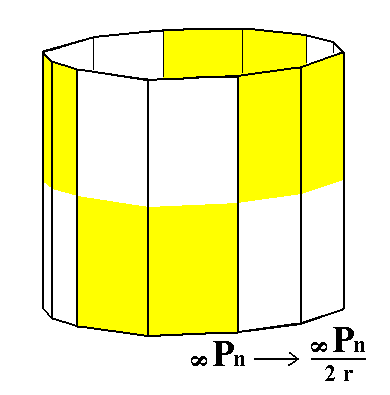Figure 5. The holohedric Dihexagonal Prism does not alter its shape when subjected to rhombohedric hemihedric, but loses some symmetry. From this rhombohedric hemihedric Dihexagonal Prism we will derive the trapezohedric tetartohedric Ditrigonal Prism (See figure 5a). |
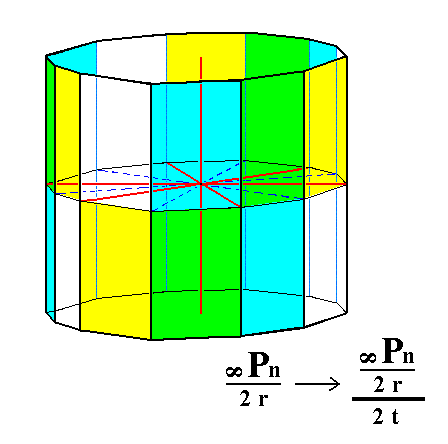
Figure 5a. Partition of the rhombohedric hemihedric Dihexagonal Prism, indicating the derivation of the trapezohedric tetartohedric Ditrigonal Prism. The coloring indicates the symmetries invoved. Two face categories, (1) the green-blue faces, and (2) the yellow-white faces, indicate the partition that expresses the trapezohedric hemihedric being applied to the rhombohedric hemihedric Dihexagonal prism. The next Figure shows the derivation of a trapezohedric tetartohedric Ditrigonal Prism.
 |
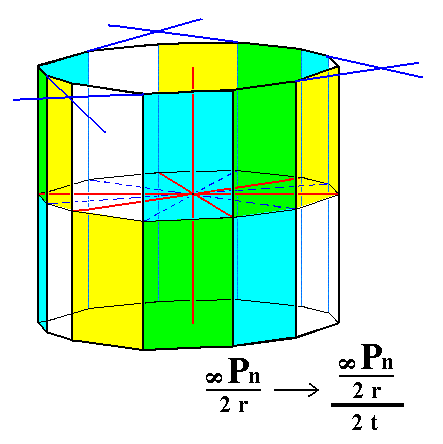Figure 5b. Initial stage of the construction (indicated by the blue lines) of a trapezohedric tetartohedric Ditrigonal Prism by the extention of (the faces of) the green-blue face category (while suppressing (the faces of) the yellow-white face category). |
 |
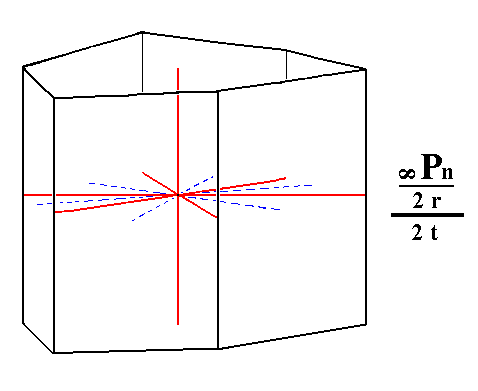Figure 5c. Result of the construction of a trapezohedric tetartohedric Ditrigonal Prism. |
From the rhombohedric hemihedric basic pinacoid we can derive the trapezohedric tetartohedric Basic Pinacoid. No change in external shape is involved. See Figure 6 and 6a.
 |
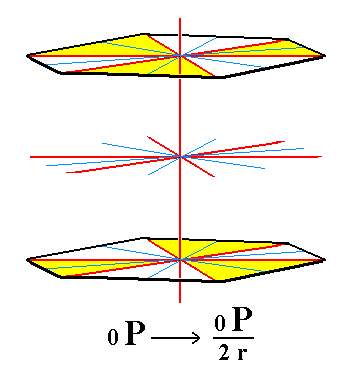Figure 6. The holohedric Basic Pinacoid does not alter its shape when subjected to rhombohedric hemihedric, but loses some symmetry. From this rhombohedric hemihedric Basic Pinacoid will be derived the trapezohedric tetartohedric Basic Pinacoid. |
 |
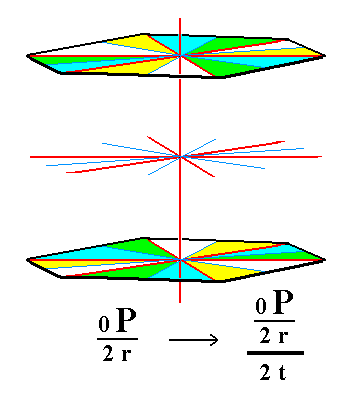Figure 6a. The trapezohedric tetartohedric Basic Pinacoid. The coloring symbolizes the symmetries invoved. |
This concludes our derivation of all the Forms of the Trigonal-trapezohedric Crystal Class by means of the merohedric approach.
All these Forms can enter in combinations with each other in real crystals.
FACIAL APPROACH
We will now derive those same Forms by subjecting the basic faces (compatible with the Hexagonal Crystal System) one by one to the symmetry operations of the present Class (the Trigonal-trapezohedric Crystal Class).
In Part One we found the following seven basic faces compatible with the Hexagonal Crystal System :
 |
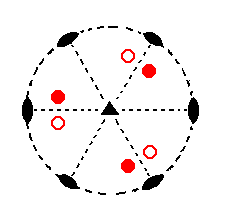Figure 7. Stereogram of the symmetry elements of the Trigonal-trapezohedric Crystal Class, and of all the faces of the most general Form. There are no mirror planes, but there are three 2-fold rotation axes coincident with the three horizontal crystallographic axes (indicated by straight dashed lines). Also a 3-fold rotation axis is present, coincident with the vertical crysallographic axis. |
The face a : ~a : -a : c generates a rhombohedron when subjected to the symmetry elements of the present Class. The generation can be imagined as follows : The face will be duplicated by the nearby 2-fold rotation axis, i.e. an image of it will be found when we rotate the face about this axis (by 1800). Then this face pair -- consisting of an upper and a lower face that are related to each other like the upper and lower parts of the letter S -- is tripled by the 3-fold rotation axis, resulting in six faces making up the rhombohedron (Figure 1).
 |
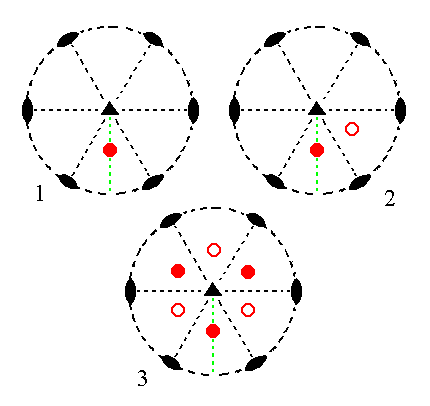Figure 8. (1). Position of the facea : ~a : -a : c in the stereogram of the symmetry elements of the Trigonal-trapezohedric Crystal Class. (2). Duplication of the face in virtue of the 2-fold rotation axis. (3). Tripling of the face pair, resulting in the Rhombohedron. |
The face 2a : 2a : -a : c generates a trigonal bipyramid when subjected to the symmetry elements of the present Class : First the face is duplicated by the nearby 2-fold rotation axis. The (rotational) image of the face lies precisely beneath it -- like the lower parts of the letter I with respect to its upper parts -- (the perpendicular of the face and the relevant 2-fold rotation axis both lie in the same vertical plane, causing the image to end up precisely beneath the initial face). Then this face pair is tripled by the action of the 3-fold rotation axis, resulting in a trigonal bipyramid. See Figure 9 in which all this is shown stereographically.
 |
Figure 9. (1). Position of the face 2a : 2a : -a : c in the stereogram of the symmetry elements of the Trigonal-trapezohedric Crystal Class. (2). Duplication of the face in virtue of the 2-fold rotation axis. (3). Tripling of the face pair, resulting in the Trigonal Bipyramid. |
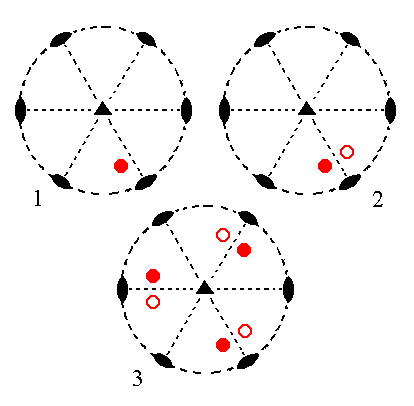
The face [3/2]a : 3a : -a : c is a definite face. Here we will consider its generalized version, namely the face [s/(s-1)]a : sa : -a : c. It will generate a Trigonal Trapezohedron (Figure 1e) when subjected to the symmetry elements of the present Class : First the face will be duplicated by a nearby 2-fold rotation axis resulting in a face pair of which the members are related to each other like the upper and lower parts in the letter S. Then this face pair will be tripled by the action of the 3-fold rotation axis, resulting in a trigonal trapezohedron. Such a trapezohedron consists, like the rhombohedron (Figure 1), of three upper and three lower faces in such a way that there is no reflectional symmetry with respect to the equatorial plane (the plane of the horizontal crystallographic axes). The trigonal trapezohedron differs from the rhombohedron by the fact that its faces are not rhombi (like they are in the rhombohedron) but irregular tetragons. This is because the generating face had a general position with respect to the crystallographic axes (and thus to the symmetry elements), while the generating face of the rhombohedron was parallel to the second horizontal crystallographic axis. All this is shown stereographically in the next Figure.
 |
Figure 10. (1). Position of the face [s/(s-1)]a : sa : -a : c in the stereogram of the symmetry elements of the Trigonal-trapezohedric Crystal Class. (2). Duplication of the face in virtue of the 2-fold rotation axis. (3). Tripling of the face pair, resulting in the Trigonal Trapezohedron. |
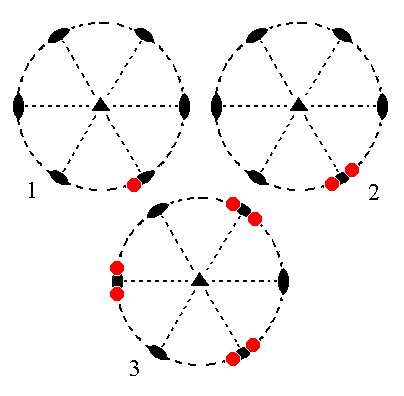
The face [3/2]a : 3a : -a : ~c is also a definite face. Here we will consider its generalized version, namely the face [s/(s-1)]a : sa : -a : ~c. It is a vertical face. It will generate a ditrigonal prism when subjected to the symmetry elements of the present Class : First the face will be duplicated by the nearby 2-fold rotation axis resulting in a vertical face pair of which the members make an angle with each other which is less than 1800. Then this face pair will be multiplied three times in virtue of the 3-fold rotation axis resulting in six vertical faces making up the ditrigonal prism. The next Figure depicts this stereographically.
 |
Figure 11. (1). Position of the face [s/(s-1)]a : sa : -a : ~c in the stereogram of the symmetry elements of the Trigonal-trapezohedric Crystal Class. (2). Duplication of the face in virtue of the 2-fold rotation axis. (3). Tripling of the face pair, resulting in the Ditrigonal Prism. |
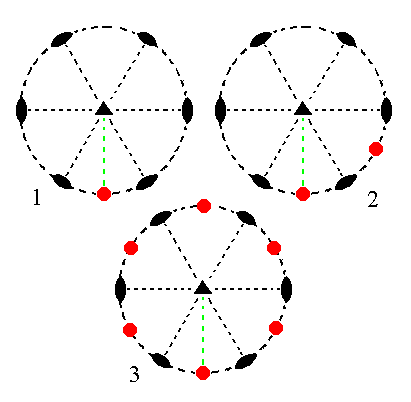
The face a : ~a : -a : ~c is also vertical. It generates a hexagonal prism when subjected to the symmetry elements of the present Class : First the face is duplicated by a nearby 2-fold rotation axis, resulting in a vertical face pair whose members make an angle smaller then 1800. This face pair is then tripled by the action of the 3-fold rotation axis resulting in six vertical faces making up the Hexagonal Prism. See Figure 12.
 |
Figure 12. (1). Position of the face a : ~a : -a : ~c in the stereogram of the symmetry elements of the Trigonal-trapezohedric Crystal Class. (2). Duplication of the face in virtue of the 2-fold rotation axis. (3). Tripling of the face pair, resulting in the Hexagonal Prism. |
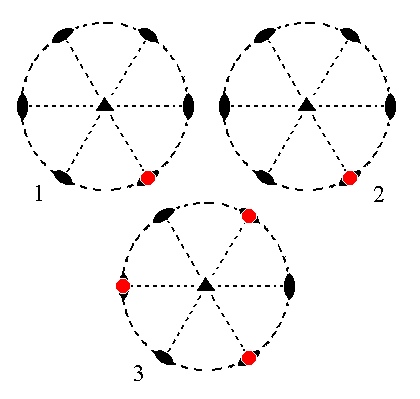
The face 2a : 2a : -a : ~c is also vertical. It generates a Trigonal Prism when subjected to the actions of the symmetry elements of the present Class : Because the face is perpendicular to its nearest 2-fold rotation axis, the action of this axis will not generate any new faces, so we still have our initial face. This face then is tripled by the action of the 3-fold rotation axis resulting in three vertical faces making up the trigonal prism. See Figure 13.
 |
Figure 13. (1). Position of the face 2a : 2a : -a : ~c in the stereogram of the symmetry elements of the Trigonal-trapezohedric Crystal Class. (2). No duplication of the face takes place by the action of the nearby 2-fold rotation axis (the axis that is perpendicular to the face), i.e. this axis does not generate new faces. (3). Tripling of the face, resulting in the Trigonal Prism. |
The face ~a : ~a : ~a : c, finally, is a horizontal face. It generates a basic pinacoid when subjected to the symmetry elements of the present Class : Any one of the 2-fold rotation axes duplicates the face, resulting in two horizontal parallel faces. The action of the 3-fold rotation axis does not add any new faces, so we end up with a Form consisting of those two horizontal parallel faces, the basic pinacoid. The next Figure depicts this stereographically.
 |
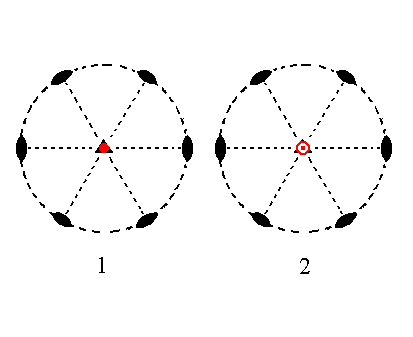Figure 14. (1). Position of the face ~a : ~a : ~a : c in the stereogram of the symmetry elements of the Trigonal-trapezohedric Crystal Class. (2). Duplication of the face takes place by the action of any 2-fold rotation axis. The action of the 3-fold rotation axis does not generate any new faces. |
This concludes our exposition of the Trigonal-trapezohedric Crystal Class, and with it our exposition of the Hexagonal Crystal System (i.e. all its twelve Classes have now been treated).
To continue, klick HERE for the Orthorhombic Crystal System