
back to homepage
The External Shapes of periodic 2-D arrays of repeated two-dimensional motifs
We continue our investigation concerning the faces, Forms and combinations of Forms in two-dimensional crystals.
In the previous Part we concluded the exposition of Class 3 belonging to the 2-D Hexagonal Crystal System.
Here we will continue our investigation by considering the next Class, namely 3m.
Hexagonal Net. (continued)
Crystals of the Class 3m have a point symmetry consisting of the
following symmetry elements :
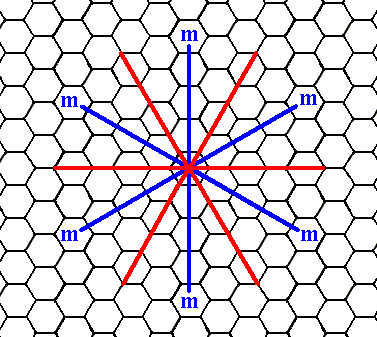
Figure 1. The symmetry elements and the system of crystallographic axes associated with the Class 3m of the 2-D Hexagonal Crystal System.
The three equivalent mirror lines are bisecting the angles of the three crystallographic axes. These crystallographic axes are (as before) chosen such that two of them lie along the edges of the rhomb-shaped unit mesh (See (1) of Figure 6 in Part Sixteen). And because the orientation of the motifs to be inserted is chosen as indicated in Figure 8, the mirror lines must be set as done in the present Figure. The 3-fold rotation axis (not indicated) is in the center of the axial system, and perpendicular to the plane of the drawing. Also the hexagonal net is given. Its building blocks have the shape of a regular hexagon.
Introduction of a face perpendicular to one of the crystallographic axes leads to its multiplication by 6 because of the presence of mirror lines (the 3-fold rotation axis is then implied). The resulting face configuration is a closed Form having the shape of a regular hexagon. See Figure 2.
Figure 2. An intitial face perpendicular to one of the crystallographic axes implies five more faces together making up a closed Form having the shape of a regular hexagon. As such it can represent a 2-D crystal of the present Class. See the next Figure.
In this image it seems that besides the 3-fold rotation axis and the three mirror lines lying between the crystallographic axes, there are still more mirror lines, mirror lines coinciding with the three crystallographic axes. But as soon as we furnish the empty building blocks with appropriate motifs (motifs that are qua symmetry consistent with the hexagonal net and with the point symmetry of our Class (3m)) the absence of the extra mirror lines will become appearant. The (outline of the) image also suggests the presence of a 6-fold rotation axis, but also here we'll see that it is just a 3-fold axis as soon as the appropriate motifs are inserted.
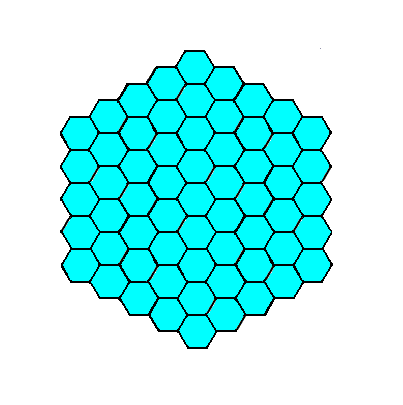
Figure 3. A two-dimensional crystal having faces as specified above. It belongs to the Class 3m of the 2-D Hexagonal Crystal System.
An introduced face parallel to one of the crystallographic axes will be multiplied by 3 in virtue of the action of the 3-fold rotation axis. The mirror lines do not multiply those faces still further, because the initial face and the two new faces are perpendicular to mirror lines, and as such already comply with the 3m symmetry. The resulting face configuration is a closed Form having the shape of an equilateral triangle. See Figures 4 and 5.
Figure 4. An initial face parallel to one of the crystallographic axes generates two more faces when subjected to the symmetry elements of the present Class (3m). The result is a closed Form having the shape of an equilateral triangle (regular trigon), and can as such represent a crystal of this Class. See the next Figure.
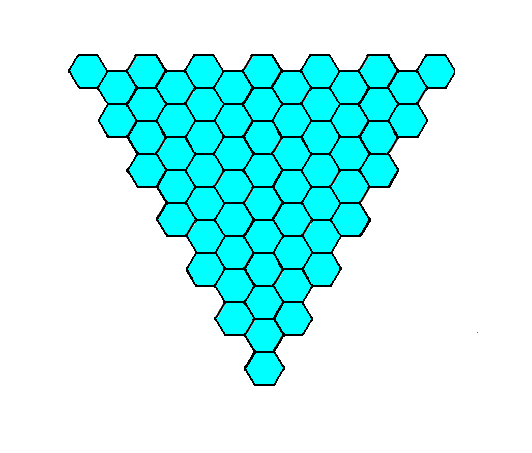
Figure 5. A two-dimensional crystal -- consisting of the faces as specified above -- of the Class 3m of the 2-D Hexagonal Crystal System.
Introducing a face that is neither perpendicular nor parallel to one of the crystallographic axes leads to yet another Form. See the next Figures.
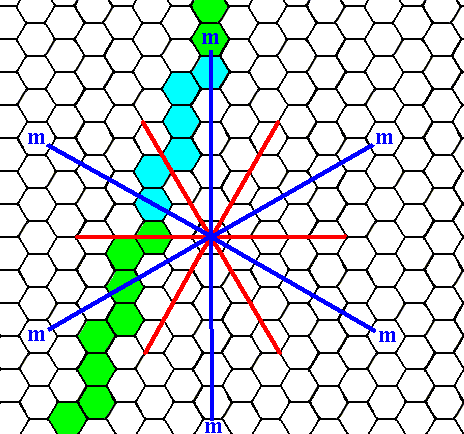
Figure 5a. A possible face that is neither perpendicular nor parallel to one of the crystallographic axes is indicated (blue and green).
We will concentrate on the blue part of it.
Introducing a face, as specified above, leads to its multiplication in virtue of the action of the mirror lines. In the next Figure the first stage of this process is given.
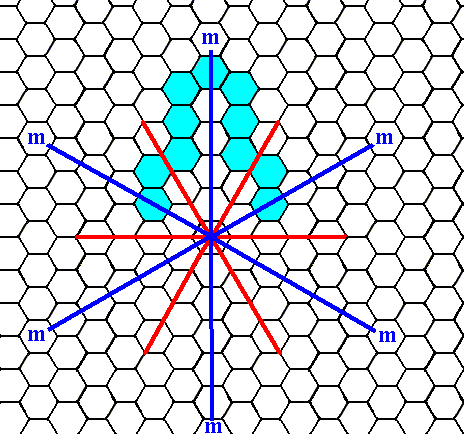
Figure 5b. The intial face (specified above) is reflected in a mirror line, resulting in two faces that are mirror images of each other.
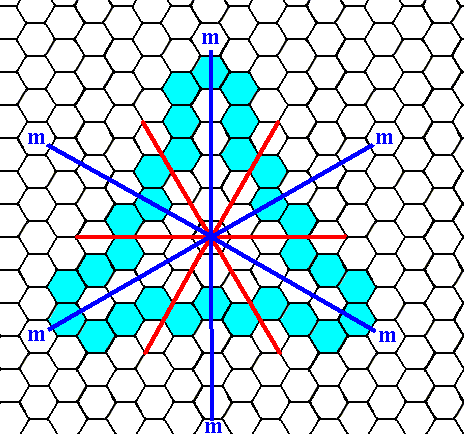
Figure 5c. When a face -- as specified above -- is subjected to the symmetry elements of the present Class, five more faces are generated by the mirror lines (the 3-fold rotation axis is then implied) resulting in a triangular figure, but with receding angles, as can be detected by the indented nature of the Figure. Such a figure is not possible in single crystals because of their energetics (A growing crystal strives to minimize its surface energy, and it can do so by minimizing its surface, because the latter contains unsatisfied or distorted chemical valences, and hence higher energies).
Our initial face turns out to be too steep. We must find a face as general with respect to its orientation as was our initial face, but instead of being steep it must be shallow. See the next Figures.
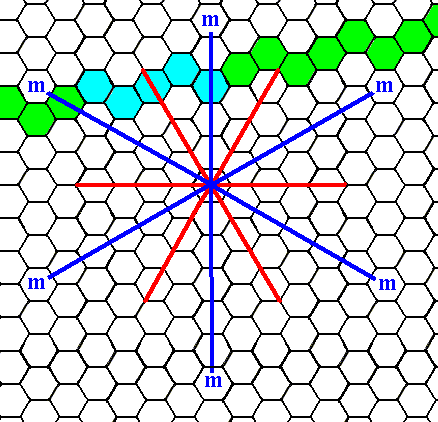
Figure 5d. An initial face with a general orientation (i.e. neither perpendicular nor parallel to one of the crystallographic axes) with a shallow slope.
We will concentrate on the blue part.
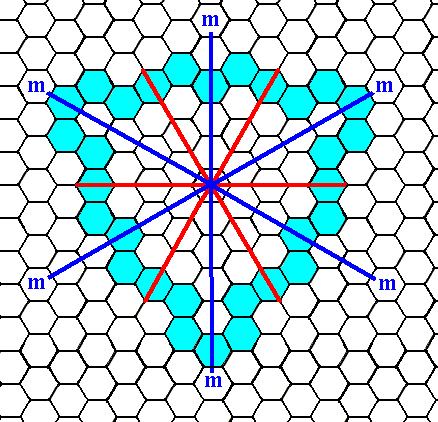
Figure 5e. When an initial face, as specified above (Figure 5d), is subjected to the symmetry elements of the present Class (3m), five new faces are generated, together making up a closed Form having the shape of a ditrigon, i.e. a six-sided figure having two types of angles, which means that two angular magnitudes (with respect to angles between the sides) are involved that alternate regularly around the figure.
As can be seen in our figure, there are no receding angles involved. So this is a genuine Form of the Class. It moreover can represent (all by itself) a crystal of that Class (See next Figure).
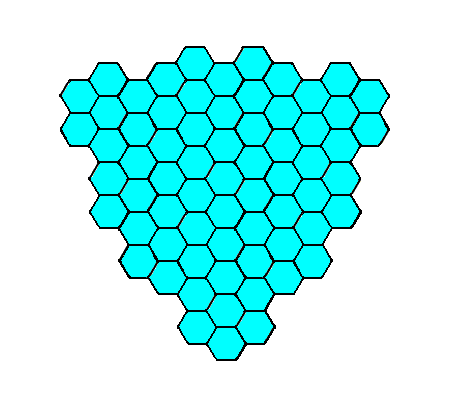
Figure 5f. A two-dimensional crystal of the Class 3m of the 2-D Hexagonal Crystal System. Its ditrigonal shape is emphasized in the next Figure.
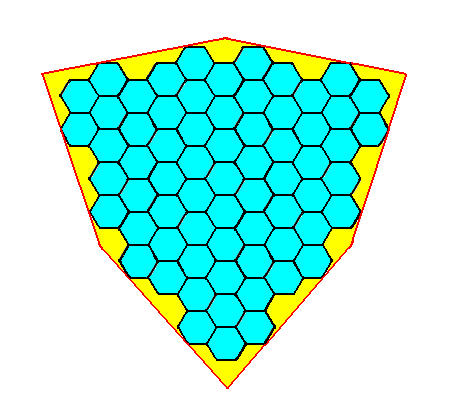
Figure 5g. The same as Figure 5f, but now with emphasis on the trigonal shape of the crystal.
The derived Forms can enter in combinations with each other. See (for an example) the next Figure.
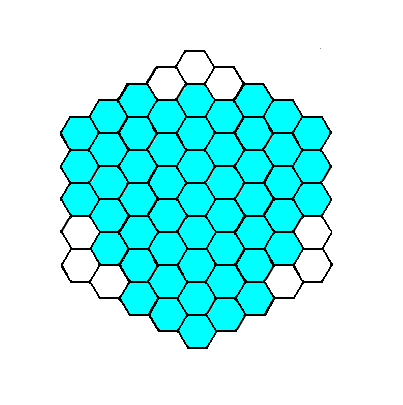
Figure 6. Indication of a possible crystal of the Class 3m , as a combination of two Forms : the one depicted in Figure 3, and the one depicted in Figure 5. The latter cuts three corners from the former as indicated. The result is presented in the next Figure.
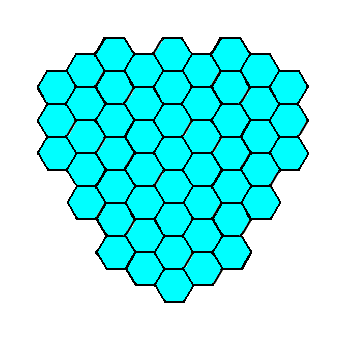
Figure 7. A two-dimensional crystal consisting of two Forms as specified above.
The present Class, 3m, admits of two Plane Groups, P3m1 and P31m, which means that two types of motifs are possible, motifs that can furnish the empty building blocks of the hexagonal net and be -- with respect to symmetry -- consistent with the point symmetry of the Class. In fact it turns out that the difference between the two types of motifs mentioned is only their orientation with respect to the crystallographic axes.
Figure 8. A periodic pattern of repeated motifs representing Plane Group P3m1. The periodic repetition is indicated by a hexagonal net drawn as a stacking of unit meshes having the shape of a rhombus.

Figure 9. Again a periodic pattern of motifs representing Plane Group P3m1.
Now a net with smaller meshes is chosen, and lines going NW--SE added, in order to outline h e x a g o n a l building blocks. For the latter see next Figure.
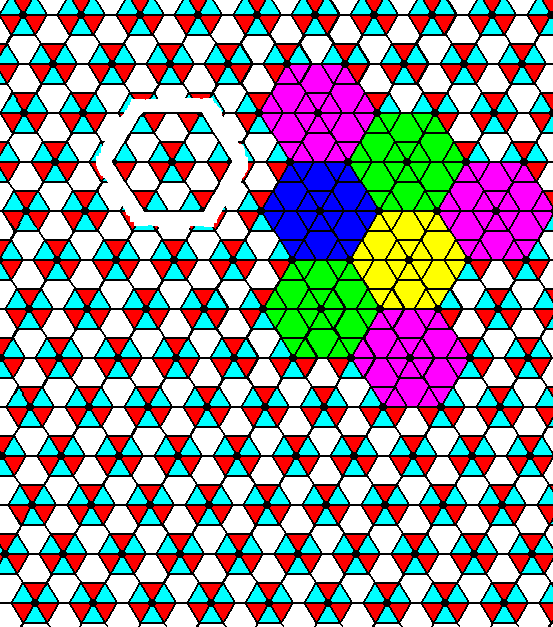
Figure 9a. As Figure 9, but now with hexagonal building blocks indicated in several ways. These hexagonal building blocks tile the plane completely.
The next Figure indicates the atomic aspect presented to the growing environment by the face on the right side of the Form derived in Figures 4 and 5.

Figure 10. The atomic aspect of the face, specified above, is indicated, but not yet fully constructed (See Figure 11). The pattern represents the Plane Group P3m1.
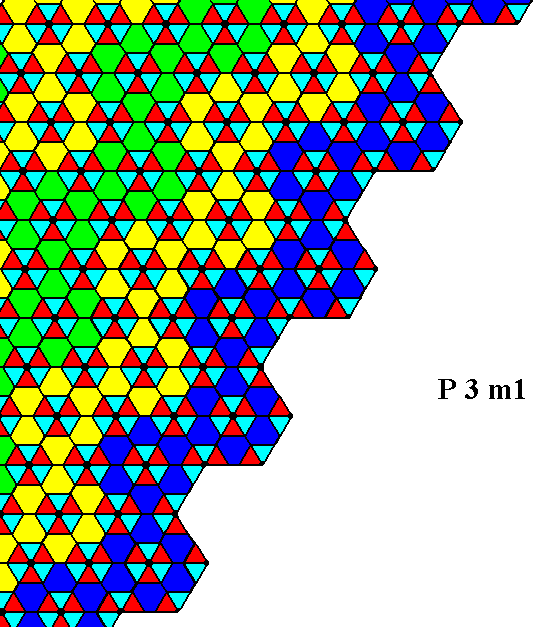
Figure 11. Atomic aspect presented to the environment (white) of the face on the right side of the Form (crystal) derived in Figures 4 and 5.
The next Figure depicts the same situation as in the previous Figure, but now with some coloration omitted in order to highlight the motifs.
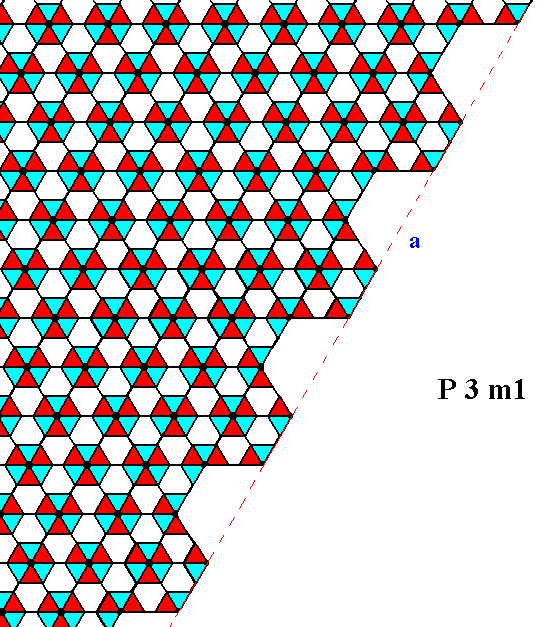
Figure 12. The atomic aspect as given in Figure 11, but with some coloration omitted, to clearly show the motifs. The face represented is indicated by a . Incomplete motifs represent unsatisfied or distorted chemical valences.
We will now have a closer look to the (point) symmetries involved in the pattern represented by the Figures 10, 11 and 12.
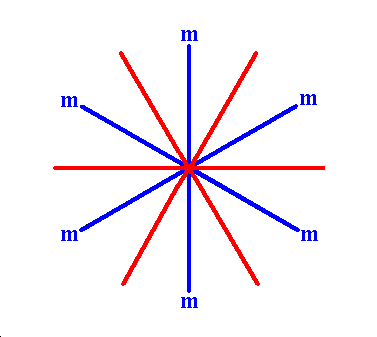
Figure 13. The system of crystallographic axes for the 2-D Hexagonal Crystal System, and the symmetry elements of the Class 3m . The 3-fold rotation axis (not explicitly indicated) goes through the point of intersection of the crystallographic axes. The three equivalent mirror lines are indicated in blue.
The pattern showing the atomic aspect (Figure 10, 11 and 12) is, as in all crystals, a periodic pattern, which means that also translational symmetries are involved, like simple translations and glide lines. This means that the symmetries, apparent in the point symmetry of the Class, are periodically repeated (See Figure 3g in Part Five). So if we want to see whether the point symmetry of the Class is indeed supported by the internal structure, we can insert the mirror lines (and the 3-fold rotation axis) of Figure 13 into the pattern. See the next Figure.
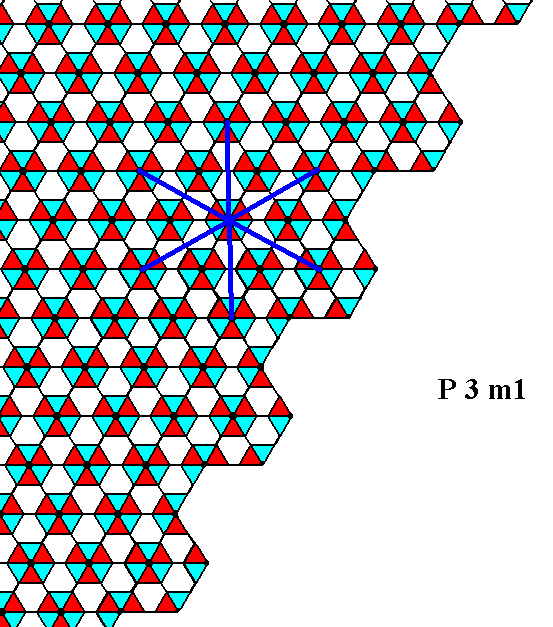
Figure 14. Insertion of the three mirror lines (blue) (Of course only their direction is important, so they can thought to be further extended ), and -- implicitly -- the 3-fold rotation axis present in the the point symmetry of the present Class, into the pattern of the Figures 10, 11 and 12.
One can clearly see that the mirror symmetry dictated by the inserted mirror lines, and also the 3-fold rotational symmetry is warranted by the internal structure. Moreover these are the only point symmetry elements supported by the structure. As can be seen there is, for example, no mirror symmetry with respect to lines that bisect the angles between the genuine mirror lines, not only with respect to the (configurarion of) faces -- as can be seen in Figure 4 -- but also not with respect to the internal structure.
The atomic aspects presented to the environment by two faces (out of six) derived in the Figures 2 and 3 are indicated in the next Figure.

Figure 15. Indication of the atomic aspects presented to the environment by two faces of the Form depicted in the Figures 2 and 3. The aspects are not yet fully constructed. The result is shown in the next Figure.
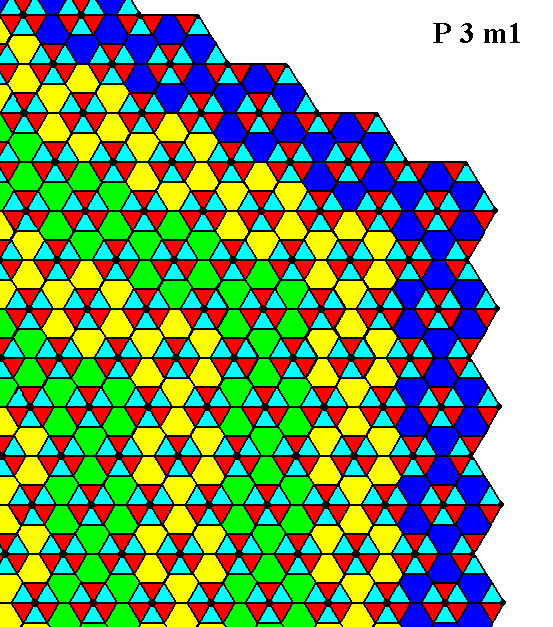
Figure 16. Atomic aspects of the faces specified above.
The next Figure depicts these same atomic aspects, but now with some coloration omitted in order to highlight the motifs.
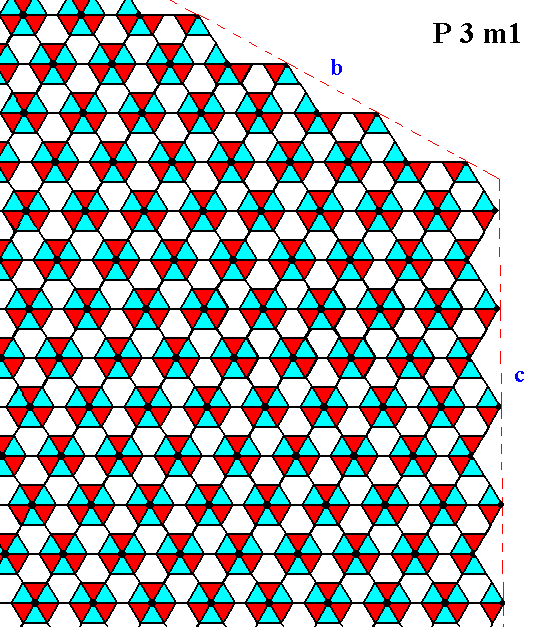
Figure 17. Atomic aspects presented to the environment of two faces (here indicated by b and c) of the Form depicted in the Figures 2 and 3. Incomplete motifs indicate unsatisfied or distorted chemical valences. The Crystal Class is 3m and the Plane Group is P3m1.
Also in this case the internal structure supports the point symmetry of the Class, and one can clearly see that, although the external shape of the crystal as depicted in the Figures 2 and 3 suggests mirror lines to be present between the three mirror lines already established, such extra mirror lines are not supported by the internal structure (the symmetry of the motifs forbids such mirror lines to be present). Also the 6-foldness of the rotation axis, suggested by the crystal's external shape, is not supported by the internal structure. See Figure 18.
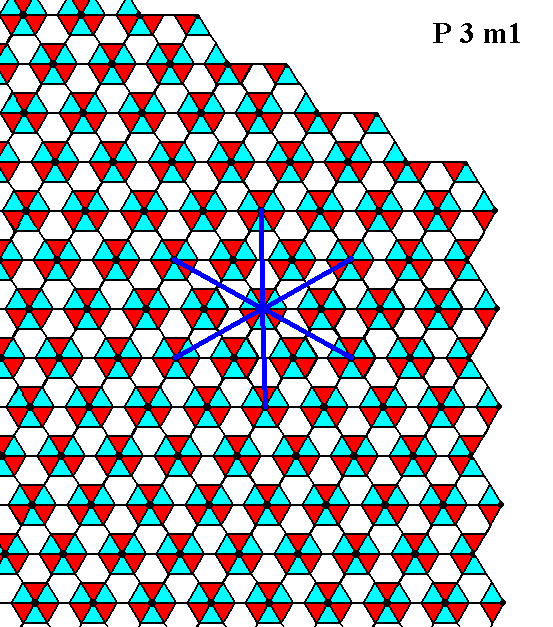
Figure 18. The point symmetry suggested by the external shape of the crystal of Figure 3 is 6mm, i.e. two sets of mirror lines (each set consisting of three equivalent mirror lines) and a 6-fold rotation axis. But the internal structure does not support such a symmetry (For example it does not support -- clearly visible when inspecting the motifs -- any mirror line perpendicular to any such face). It shows that the point symmetry of the crystal is in fact 3m, i.e. one set of mirror lines (that set consisting of three equivalent mirror lines) and one 3-fold rotation axis. In real crystals the absence of certain symmetries, symmetries suggested by the external shape, will be detected by a corresponding different chemical or physical behavior of the faces involved. In the present Figure the actually existing mirror lines, associated with the point symmetry of our Class, are inserted (blue).
The next Figure shows that the 6-fold rotation axis as suggested by the crystal of Figure 3 is not supported by the internal structure of our pattern under investigation. It is, instead, a 3-fold rotation axis.
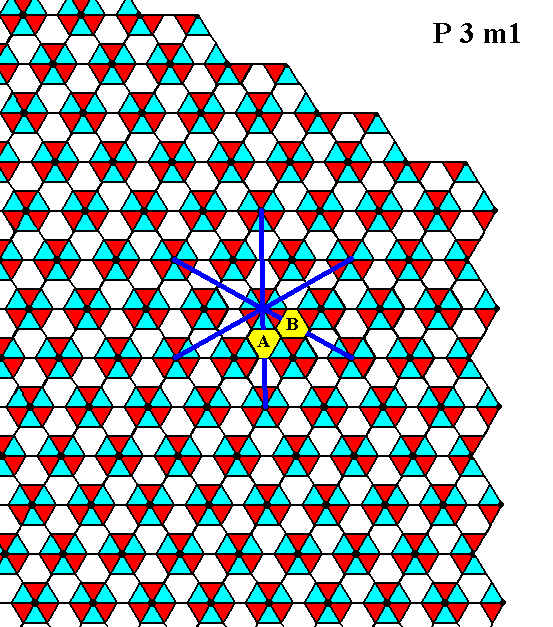
Figure 18a. The pattern of Figure 18 does not support a 6-fold rotation axis, but instead a 3-fold rotation axis. The absence of 6-fold rotational symmetry is apparent when one looks to the two triangles indicated by A and B (each consisting of the yellow area and three smaller triangles. These two triangles are different, as can be seen by the coloration (of the smaller triangles), so a 600 rotation will not map the structure onto itself, while a 300 rotation does.
In the next Figures we give the atomic aspect presented to the environment by the face established in Figure 5d, and present in the Figures 5e, 5f and 5g.
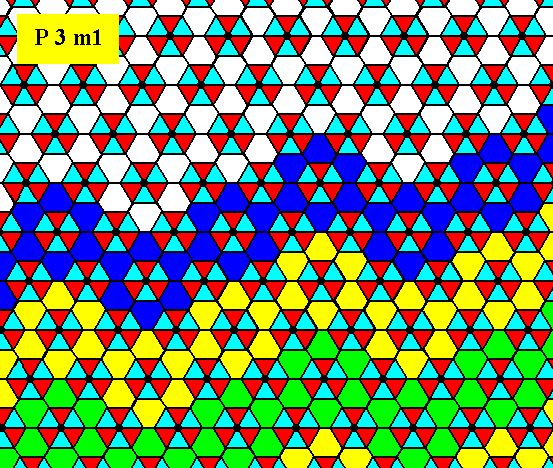
Figure 19. Indication -- but not yet a full construction -- of the atomic aspect presented to the environment by the face established in Figure 5d. The pattern represents the Plane Group P3m1.
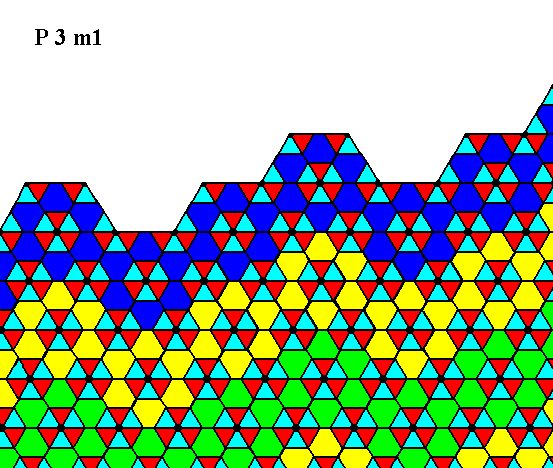
Figure 20. Atomic aspect presented to the environment by the face specified above.
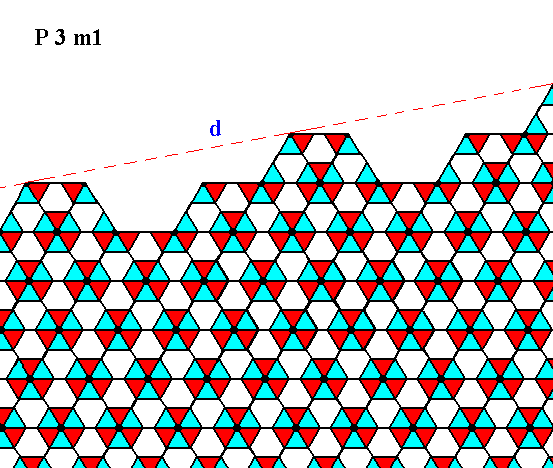
Figure 21. The same as Figure 20, but now with some coloration removed in order to highlight the motifs. The face is indicated by d. Incomplete motifs indicate unsatisfied or distorted chemical valences.
The next (and last) Plane Group of our Class 3m we're going to consider is the Plane Group P31m. We'll do this in the next Part.
To continue, click HERE for Part Eighteen.
back to homepage