
back to homepage
The External Shapes of periodic 2-D arrays of repeated two-dimensional motifs
We continue our investigation concerning the faces, Forms and combinations of Forms in two-dimensional crystals.
Hexagonal Net (continued).
In the previous Part we concluded the exposition of 2-D crystals belonging to the Class 3m, and its Plane Groups P3m1 and P31m.
Now we will turn our attention to the next Class of the 2-D Hexagonal Crystal System, namely the Class 6.
The only symmetry element of this Class is a 6-fold rotation axis (thought to run perpendicular to the (2-D) plane).
The next Figure depicts the hexagonal net, the system of crystallographic axes and the 6-fold rotation axis. The hexagonal net is drawn such that one can recognize hexagonal building blocks in it. Two of the crystallographic axes go along two edges of the rhomb-shaped unit mesh (not drawn).
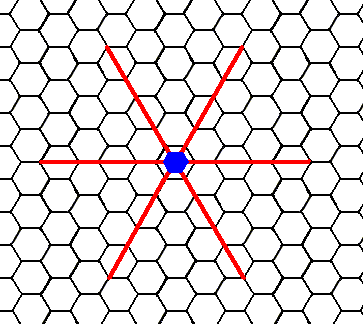
Figure 1. Hexagonal net, axial system (red) and 6-fold rotation axis.
The 6-fold rotation axis, perpendicular to the plane of the drawing, is indicated by a small solid blue hexagon. This rotation axis is the only symmetry element of the present Class (6).
We're now going to derive the possible Forms of this Class.
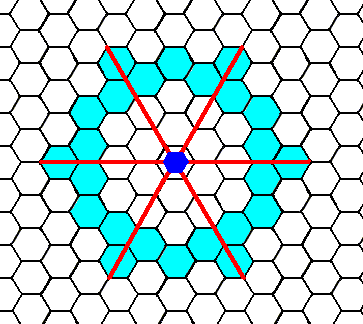
Figure 2. When an intial face, parallel to one of the crystallographic axes, is subjected to the symmetry element of the present Class (i.e. subjected to the 6-fold rotation axis), five more faces will be generated making up a closed Form consistent with the symmetry of the present Class, and having the shape of a regular hexagon that can represent a crystal of our Class.
Of course also larger hexagons can be constructed this way -- all such hexagons are equivalent, i.e. they all belong to the same Form -- as the next Figure shows.
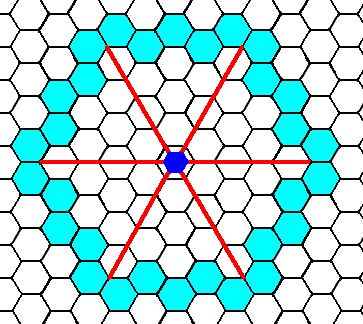
Figure 3. An initial face (here a little farther away from the center of the axial system than was the case in the previous Figure) implies five more (equivalent) faces in virtue of the action of the 6-fold rotation axis. The resulting Form has again the shape of a regular hexagon and can represent a crystal of the present Class.
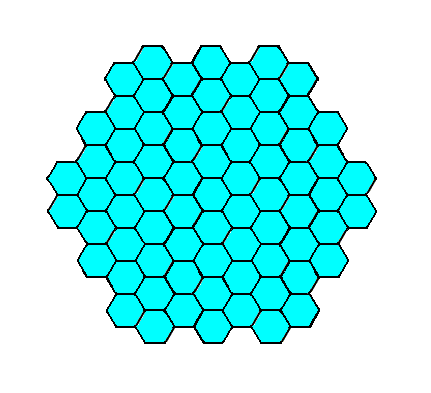
Figure 4. A two-dimensional crystal of the Class 6 of the 2-D Hexagonal Crystal System, according to Figure 3. As drawn it consists of a stacking of yet empty building blocks, causing it to have a higher symmetry than that of its Class -- in the drawing of the crystal one can detect mirror lines -- but as soon as the building blocks are furnished with the appropriate motifs the crystal will not display those extra symmetry elements anymore. It will fully comply with the symmetry of its Class.
Introducing a face perpendicular to one of the (equivalent) crystallographic axes leads to a multiplication of that face by 6, resulting in a closed Form having the shape of a regular hexagon that can represent a crystal of this Class. See the next two Figures.
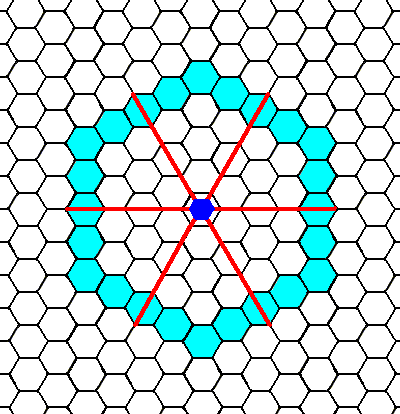
Figure 5. When an initial face is subjected to the symmetry element of the present Class, five more faces are generated making up a closed Form having the shape of a regular hexagon.
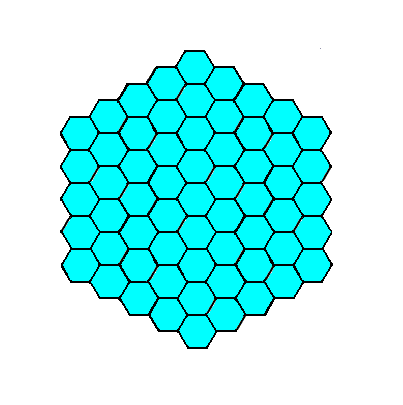
Figure 6. A two-dimensional crystal according to Figure 5.
Also here more symmetry is implied than that of the present Class. The real symmetry will become appearant when the empty building blocks are furnished with the appropriate motifs.
The next possible face (possible, because it can be constructed as the edge of a stack of hexagonal building blocks) is neither parallel nor perpendicular to any of the crystallographic axes. It is constructed in the next Figure.
Figure 6a. A possible face. It is neither parallel nor perpendicular to any of the crystallographic axes. We will concentrate on the blue part.
The axial system is given in red. The 6-fold rotation axis -- as the only symmetry element of the present Class (6) -- is indicated by a small solid blue hexagon. This axis is perpendicular to the plane of the drawing.
Introducing a face as specified above, leads to its multiplication by 6, in virtue of the 6-fold rotation axis, resulting in a Form of this Class. The first stage of this generation is depicted in the next Figure.
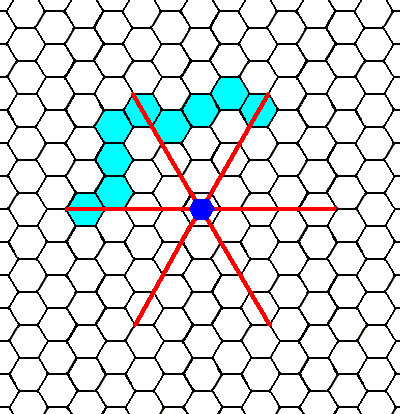
Figure 6b. An initial face (blue part in Figure 6a) is multiplied by the action of the 6-fold rotation axis. The first stage of this is depicted here, i.e. a second face is generated from the initial one. The next Figure finishes this construction.
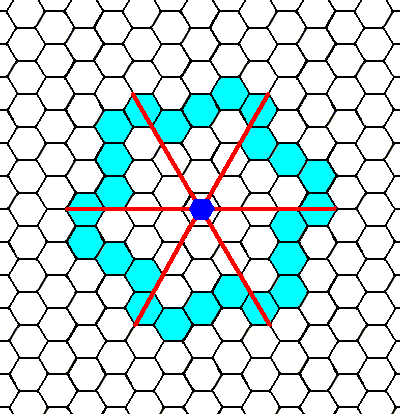
Figure 6c. When a face, as specified above, is subjected to the symmetry element of the present Class, five more faces are generated together making up a closed Form having the shape of a regular hexagon. It can represent a crystal of this Class (See next Figure).
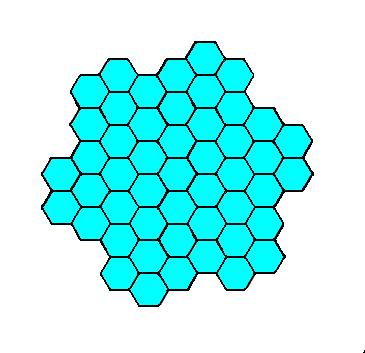
Figure 6d. A two-dimensional crystal of the Class 6 of the 2-D Hexagonal Crystal System. The hexagonal shape of this crystal is emphasized in the next Figure.
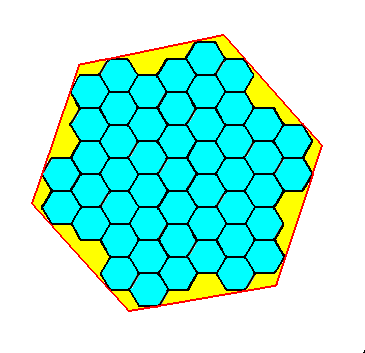
Figure 6e. The same as Figure 6d, but now with the hexagonal shape of the crystal emphasized.
These Forms can enter in combinations with each other as the next two Figures illustrate.
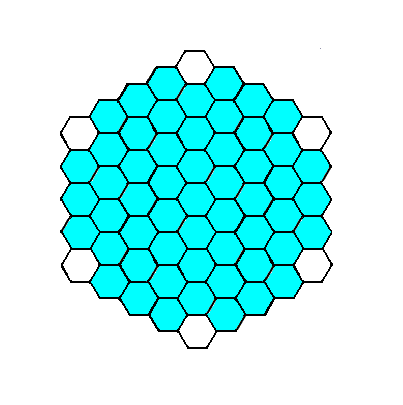
Figure 7. When a Form, equivalent to the one in Figure 6 combines itself with a Form equivalent to the one in Figure 4, a crystal like the one indicated could be the result : the corners of one hexagon are chopped off by another hexagon (See also the next Figure).

Figure 8. A two-dimensional crystal of the Class 6 of the 2-D Hexagonal Crystal System. The crystal consists of two interpenetrating Forms.
We are now ready to investigate the atomic aspects presented to the environment by the possible crystal faces of the present Class (6). In order to do so we must consider the relevant Plane Groups. The present Class is connected to only one Plane Group, namely P6.
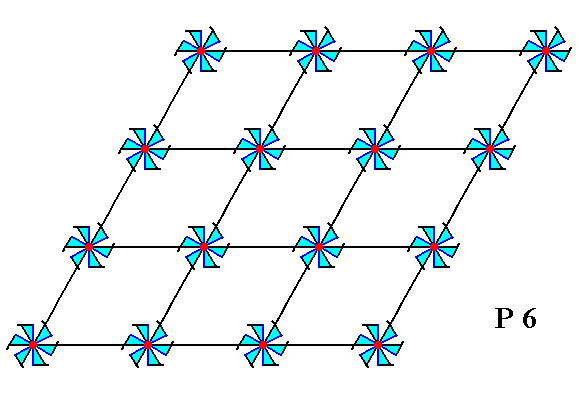
Figure 9. A periodic pattern of motifs representing Plane Group P6.
The hexagonal net is drawn such as to indicate romb-shaped unit meshes.
The next Figure gives this same periodic pattern, but now using a smaller mesh and having inserted diagonal NW--SE lines to indicate h e x a g o n a l building blocks.

Figure 10. A periodic pattern of motifs representing Plane Group P6.
The hexagonal net is drawn such that hexagonal building blocks can be indicated (Some of them are highlighted).
The atomic aspect presented to the growing environment by the top face of the Form of Figure 4 is drawn in the next Figures.

Figure 11. Indication -- but not yet a full construction -- of the atomic aspect presented to the environment by the top face of the Form in Figure 4. The other faces of this Form are equivalent (They are equivalent by definition : A Form is a face configuration having the symmetry of its Class and consisting of equivalent faces). The face belongs to a 2-D crystal of Class 6, and its structure represents Plane Group P6.

Figure 12. Atomic aspect presented to the environment by the top face of the Form in Figure 4.

Figure 13. The same as Figure 12, but now with some coloration removed in order to highlight the motifs. The face is indicated by a . Incomplete motifs indicate unsatisfied or distorted chemical valences.
In the next Figures we consider the atomic aspect presented to the growing environment by the upper right face of the Form depicted in Figure 6.

Figure 14. Indication -- not yet a full construction -- of the atomic aspect presented to the environment by the upper right face of the Form in Figure 6.
The Class is 6, and the Plane Group is P6.
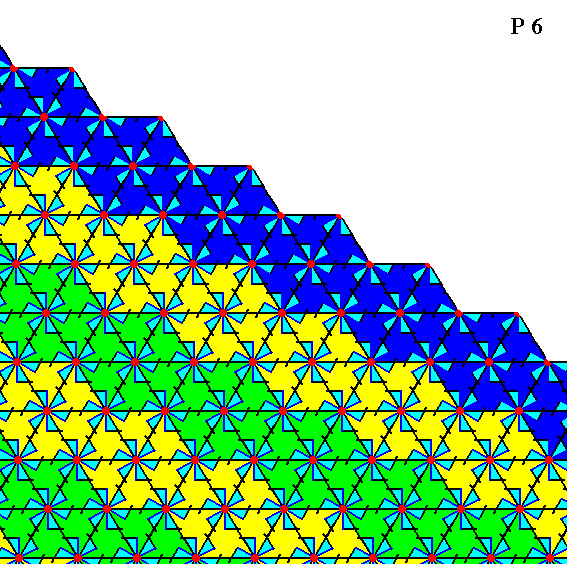
Figure 15. Atomic aspect presented to the environment by the face specified above.
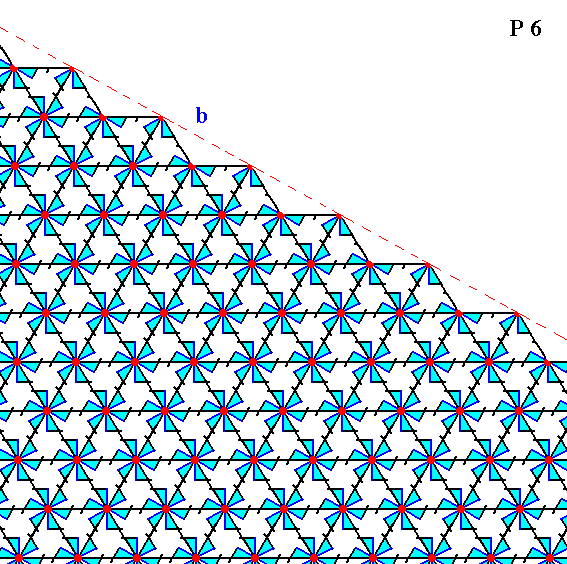
Figure 16. The same as Figure 15, but now with some coloration removed in order to highlight the motifs. Incomplete motifs indicate unsatisfied or distorted chemical valences. The face is indicated by b.
The next Figures consider the atomic aspect presented to the environment by the face depicted in Figure 6a, and present in the Figures 6b, 6c, 6d and 6e.

Figure 17. Indication -- but not yet a full construction -- of the atomic aspect presented to the environment by the face depicted in Figure 6a.
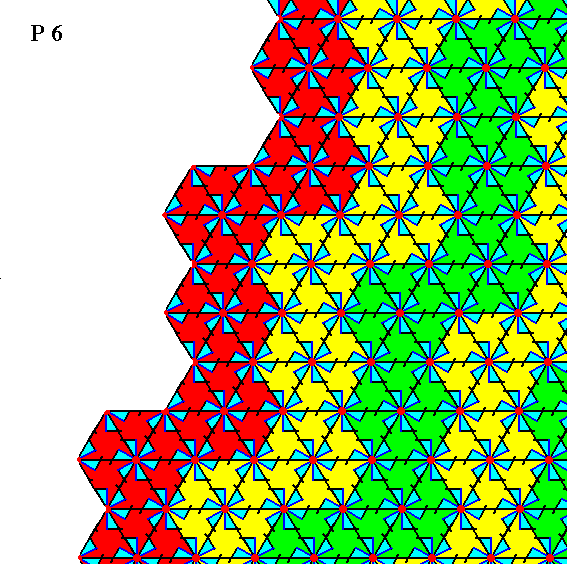
Figure 18. Atomic aspect presented to the environment by the face specified above.
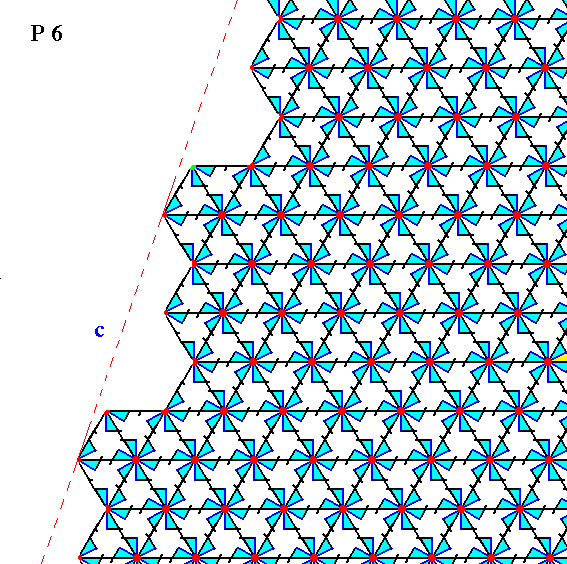
Figure 19. The same as Figure 18, but now with some coloration removed in order to highlight the motifs. The face is indicated by c. Incomplete motifs indicate unsatisfied or distorted chemical valences.
Although some Forms of this Class, namely the ones depicted in the Figures 4 and 6, suggest the presence of mirror lines, the internal structure -- as depicted in the Figures 13 and 16 -- prohibits any mirror lines to be present, so the point symmetry of such crystals is lower than their external shape would suggest. In the Form depicted in the Figures 6d and 6e this absence of mirror lines is already apparent in the ordering of empty building blocks.
This concludes our exposition of the Class 6 of the 2-D Hexagonal Crystal System.
The next (and) last Class of this System is 6mm. We will consider it in the next Part.
To continue, click HERE for Part Twenty.
back to homepage