
back to homepage
The External Shapes of periodic 2-D arrays of repeated two-dimensional motifs
We continue our investigation concerning the faces, Forms and combinations of Forms in two-dimensional crystals.
Hexagonal Net (continued).
In the previous Part we concluded the exposition of 2-D crystals belonging to the Class 6, and its Plane Group P6.
Now we will turn our attention to the next (and last) Class of the 2-D Hexagonal Crystal System, namely the Class 6mm.
The point symmetry elements of the Class 6mm are the following :
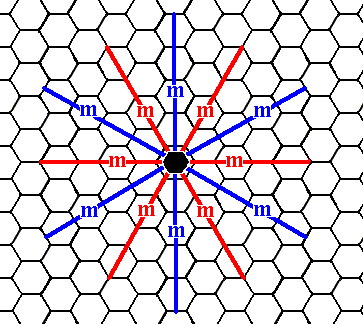
Figure 1. Symmetry elements of the Class 6mm of the 2-D Hexagonal Crystal System.
Three mirror lines (m) coinciding with the three crystallographic axes (red).
Three mirror lines (m) lying exactly between the mirror lines of first set.
One 6-fold rotation axis perpendicular to the plane of the drawing and located at the point of intersection of the crystallographic axes. It is indicated by a small solid black hexagon.
The hexagonal net is drawn such that hexagonal building blocks are highlighted.
The origin of the axial system lies in the center of a hexagonal building block.
Introducing a face parallel to one of the (equivalent) crystallographic axes leads to the generation of five more faces in virtue of the actions of the mirror lines. The 6-fold axis is then implied. The result is a closed Form having the shape of a regular hexagon. See Figure 2.
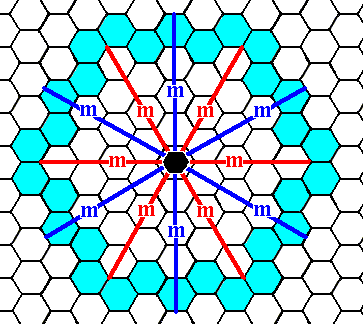
Figure 2. When an initial face, parallel to one of the crystallographic axes, is subjected to the symmetry elements of the present Class (6mm), five more faces are generated making up a closed Form having the shape of a regular hexagon, that can represent a crystal of this Class (See next Figure).
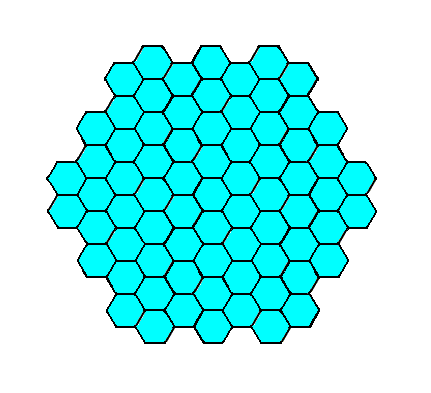
Figure 3. A two-dimensional crystal of the Class 6mm .
This crystal looks the same as the one depicted in Figure 4 in Part Nineteen. But after their internal structure is revealed their different symmetries will become apparent.
Introducing a face perpendicular to one the (equivalent) crystallographic axes leads to the generation of five more faces in virtue of the action of the mirror lines. The result is a closed Form having the shape of a hexagon, but with a different orientation (with respect to the axial system) from that of the previous Form.
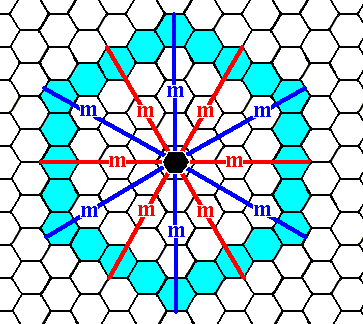
Figure 4. When an initial face, perpendicular to one of the crystallographic axes, is subjected to the symmetry elements of the present Class, five more faces are generated making up a closed Form having the shape of a regular hexagon and that can represent a crystal of this Class (See next Figure).
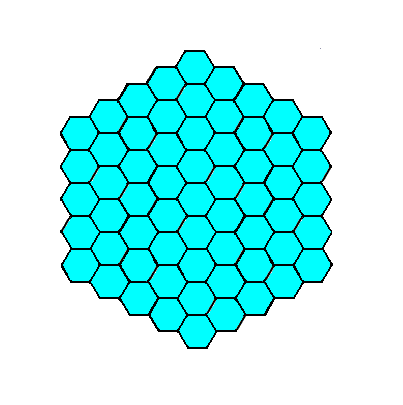
Figure 5. A two-dimensional crystal of the Class 6mm of the 2-D Hexagonal Crystal System.
Although this crystal looks the same as the one depicted in Figure 6 in Part Nineteen, their different symmetries will become apparent when their internal structure is examined.
Another possible face is one that is neither parallel nor perpendicular to any of the crystallographic axes. It is depicted in the next Figure.
Figure 6. A possible face, having a general orientation, which here means that it is neither parallel nor perpendicular to any of the crystallographic axes.
We will concentrate on the blue part of it.
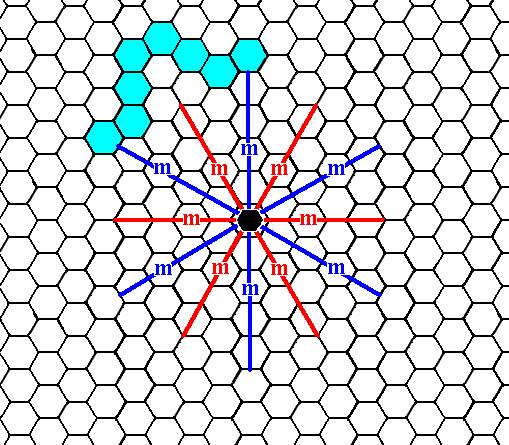
Figure 7. The initial face, as specified above, is multiplied by the symmetry elements of the present Class (6mm). The first stage is given here : The initial face (blue part in Figure 6) is duplicated by a mirror line.
The next Figure gives the full construction of the resulting face configuration.
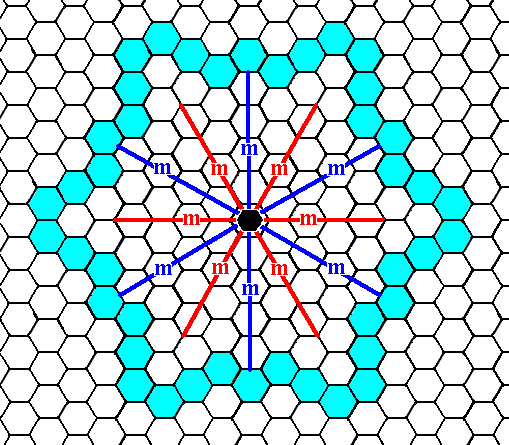
Figure 8. When an initial face, specified above, is subjected to the symmetry elements of the present Class, a configuration of 12 faces will be the result. But this configuration cannot be a genuine Form because it contains receding angles. So the initial face should have another orientation but still be a general face, i.e. a face that is neither perpendicular nor parallel to any of the crystallographic axes. The next Figure depicts such a face.
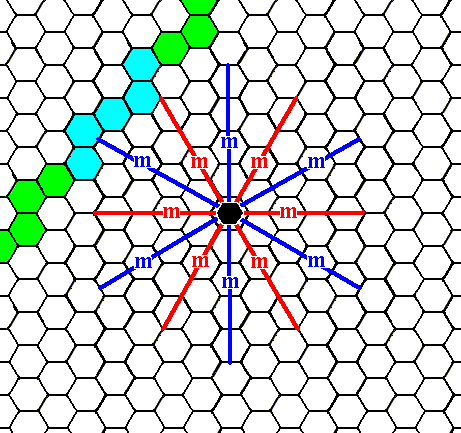
Figure 9. A possibe (general) face that is neither perpendicular nor parallel to any of the crystallographic axes, and that has a different orientation as that of the face depicted in Figure 6. We will concentrate on the blue part.
We will now derive the Form from this face (See the next Figures).
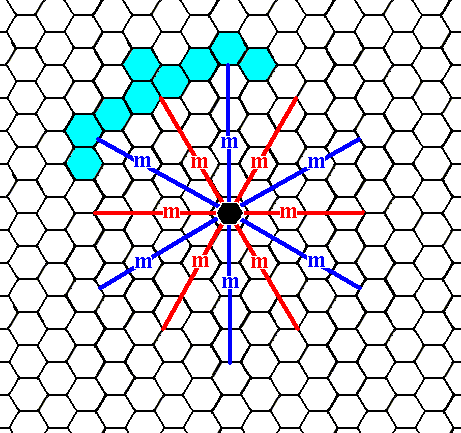
Figure 10. When an initial face, specified above, is subjected to the symmetry elements of the present Class, it will be multiplied. The first stage is given here : The initial face is duplicated by a mirror line. The full construction of the face configuration is given in the next Figure.
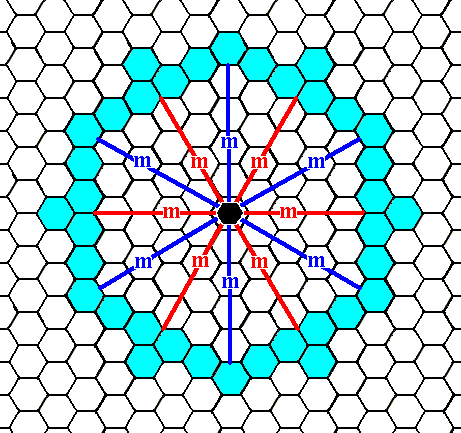
Figure 11. When an initial face, as specified above, is subjected to the symmetry elements of the present Class it will be multiplied 12 times, resulting in a closed Form having the shape of a dihexagon, i.e. a figure with 12 equal sides but with angles alternating between two values. As can be seen, there are no receding angles, so this is a genuine Form of our Class, and because it is closed it can represent a crystal of this Class (See next Figures).
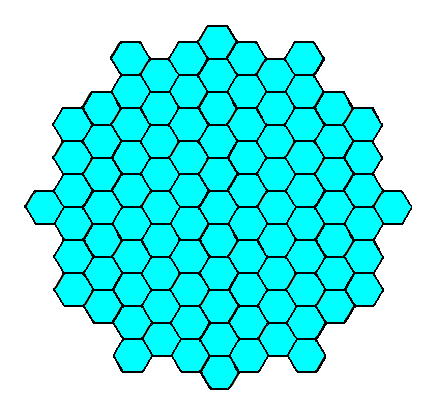
Figure 12. A two-dimensional crystal of the Class 6mm of the 2-D Hexagonal Crystal System. It has the shape of a dihexagon. This shape is emphasized in the next Figure.
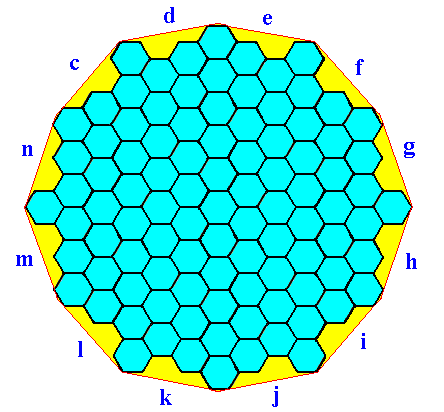
Figure 13. The dihexagonal shape of the crystal of Figure 12 is emphasized.
These Forms can enter in combinations with each other, as exemplified in the next Figures.
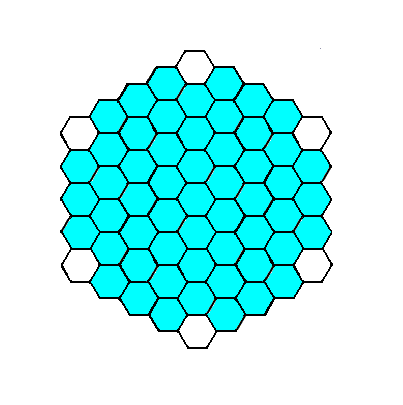
Figure 14. Construction of a combination of two Forms, equivalent to the Forms depicted in the Figures 3 and 5. The result is depicted in the next Figure.

Figure 15. A crystal of the Class 6mm of the 2-D Hexagonal Crystal System. It consists of a combination of two Forms.
The next Figure highlights the twelve faces of this combination.
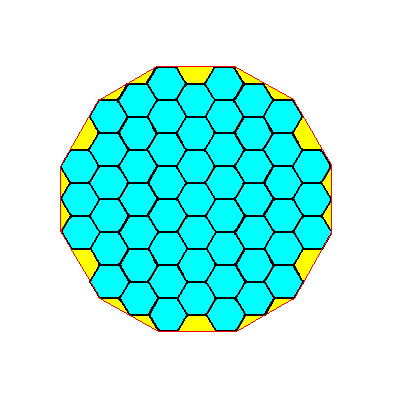
Figure 15a. The crystal of Figure 15, but now with its 12 faces highlighted.
We can now investigate the atomic aspects presented to the growing environment by the faces established above.
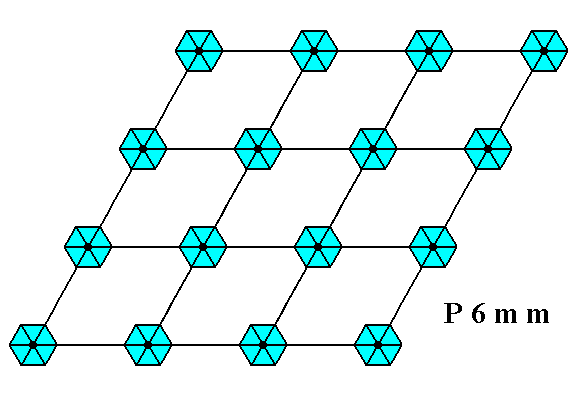
Figure 16. A pattern of repeated motifs representing Plane Group P6mm .
The net is drawn such that the rhomb-shaped unit meshes are apparent.
The next Figure depicts this same pattern, but now using smaller meshes. Moreover NW--SE lines are added to the net in order to visualize h e x a g o n a l building blocks.
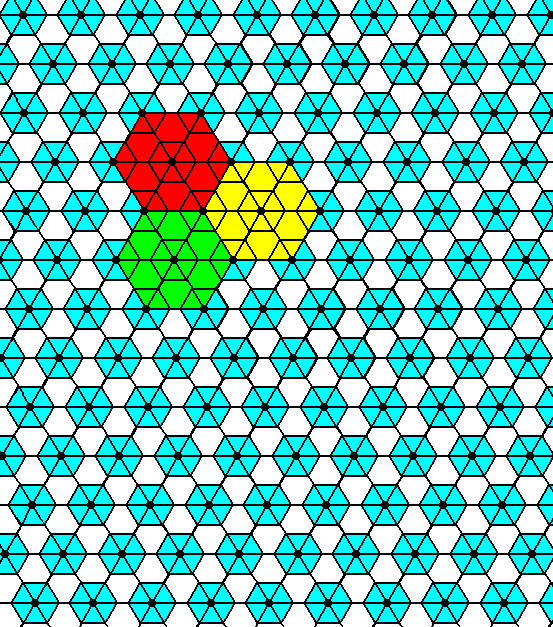
Figure 17. A periodic pattern of motifs representing Plane Group P6mm .
Hexagonal building blocks can clearly be discerned (three are highlighted).
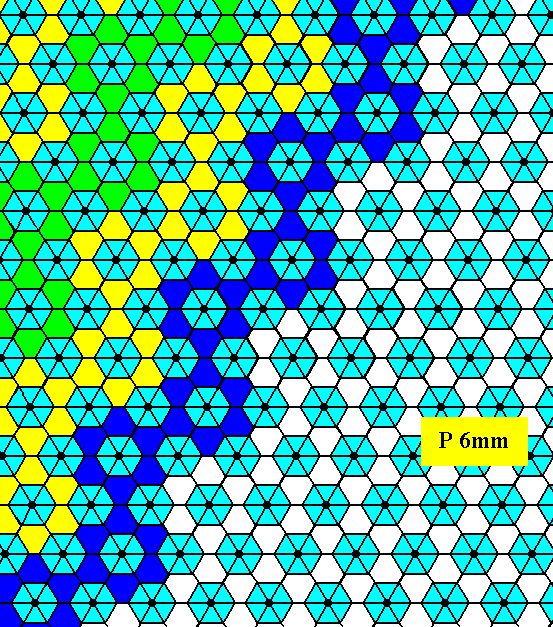
Figure 18. Indication -- not yet a full construction -- of the atomic aspect presented to the environment by the lower right face depicted in Figure 3.
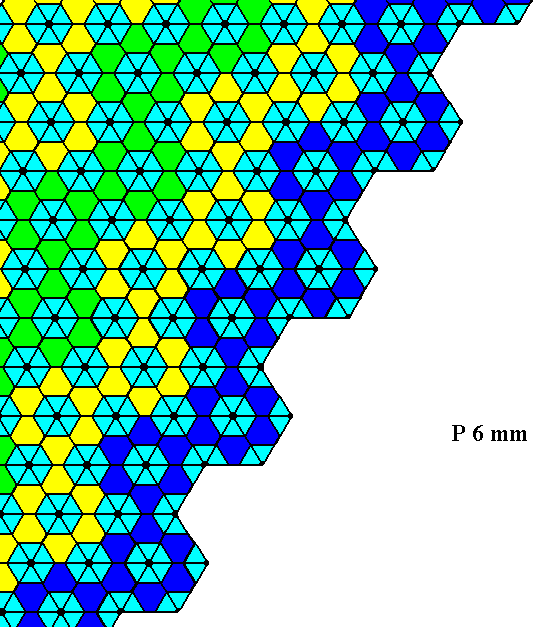
Figure 19. Atomic aspect presented to the environment by the face specified above.
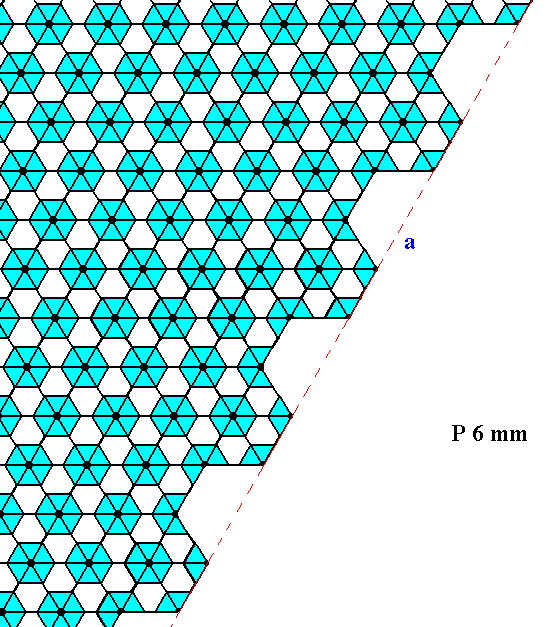
Figure 20. The same as Figure 19, but now with some coloration removed in order to highlight the motifs. The face is indicated by a . Incomplete motifs indicate unsatisfied or distorted chemical valences.
The atomic aspect presented to the environment by the upper right and right faces of the Form depicted in Figure 5 is considered in the next Figures.
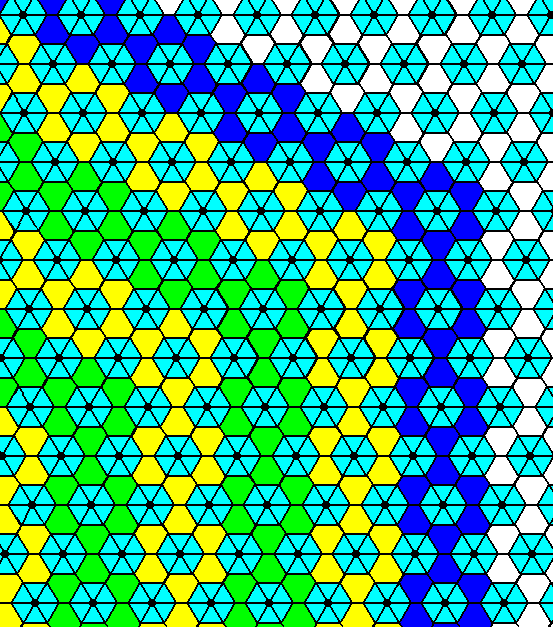
Figure 21. Indication -- not yet a full construction -- of the atomic aspect of two faces of the Form depicted in Figure 5.
The Class is 6mm, the Plane Group is P6mm.
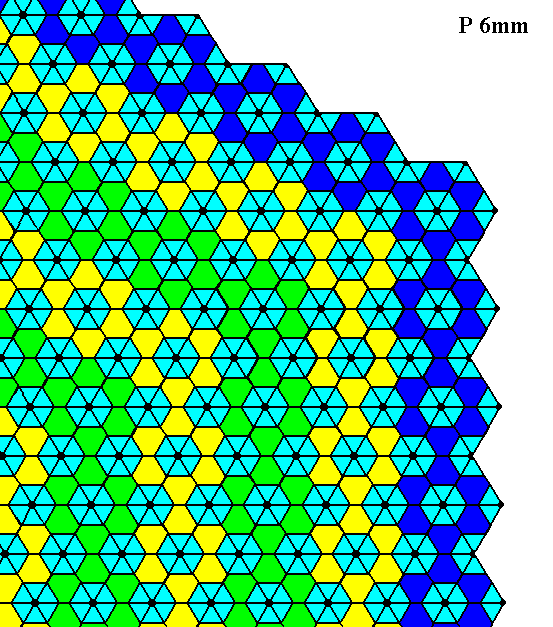
Figure 22. Atomic aspect of two faces of the Form depicted in Figure 5.
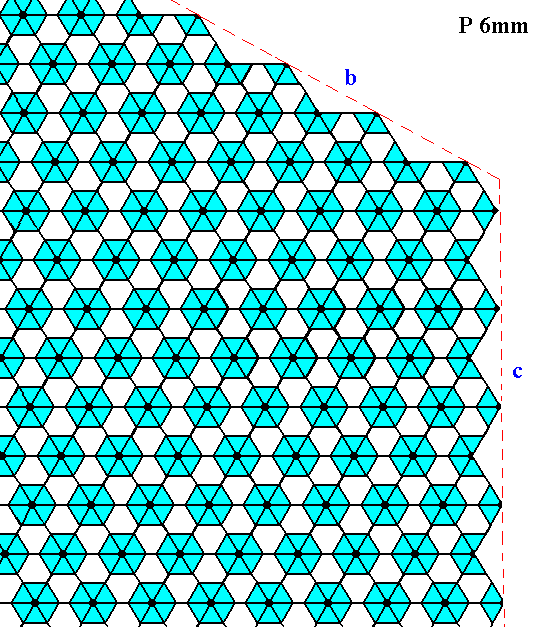
Figure 23. The same as Figure 22, but now with some coloration removed in order to highlight the motifs. The faces are indicated by b and c. Incomplete motifs indicate unsatisfied or distorted chemical valences.
The atomic aspect of the face depicted in Figure 9, and present in the Form given in the Figures 11, 12 and 13, is considered in the next Figures.
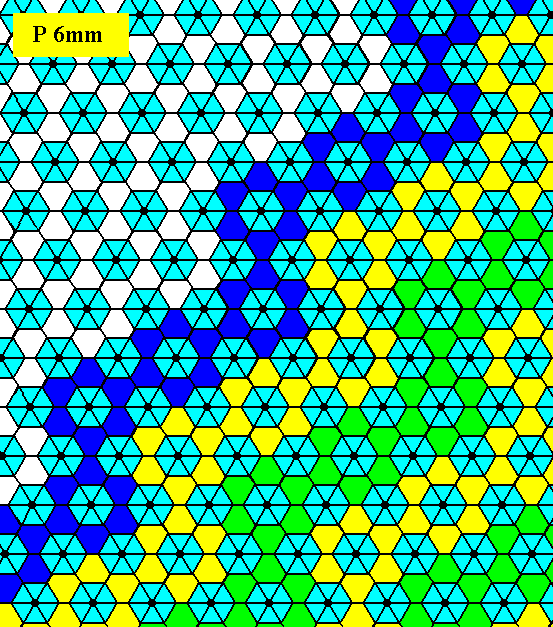
Figure 24. Indication -- not yet a full construction -- of the atomic aspect of the face depicted in Figure 9.
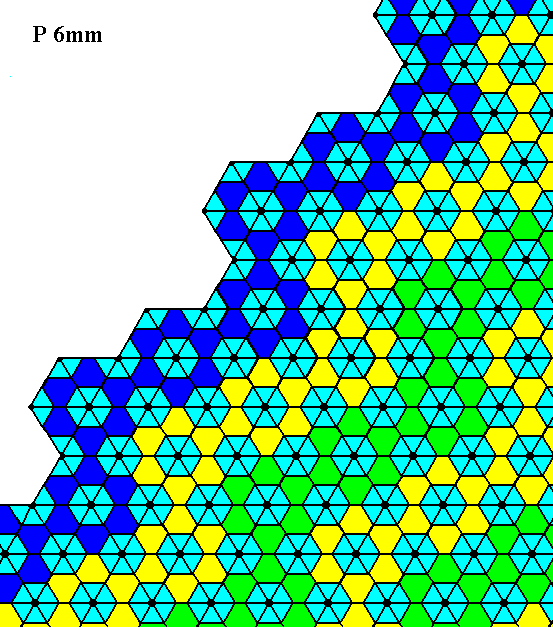
Figure 25. Atomic aspect of the face specified above.
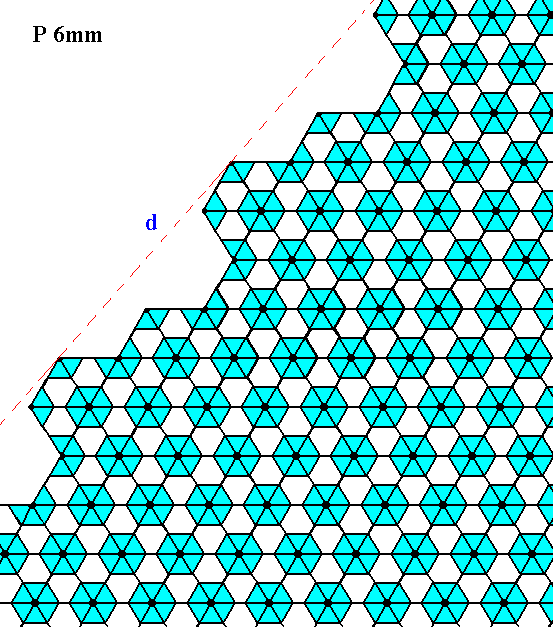
Figure 26. The same as Figure 25, but now with some coloration removed in order to highlight the motifs. The face is indicated by d. Incomplete motifs indicate unsatisfied or distorted chemical valences.
This concludes our exposition of the Class 6mm, and with it our exposition of the 2-D Hexagonal Crystal System. This moreover was the last 2-D Crystal System to be explained, which means that we have completed our exposition of all two-dimensional Crystal Classes and Systems.
The reason why we discussed the crystallography of two-dimensional crystals at length is to obtain insight in the dependence of faces and Forms -- and that means (of) the symmetry and intrinsic shapes -- of crystals on their internal structure : These dependence relations are, in the case of two-dimensional crystals relatively easy to grasp and to draw. And because three-dimensional crystals behave largely in the same way, we now at the same time have obtained some insight in the way they get their symmetries and shapes. The symmetries and shapes of three-dimensional crystals also are dependent on their internal structure, in the way as we see it in two-dimensional crystal, but the third dimension brings with it some extra features that do not occur in 2-D crystals, for instance the occurrence of screw axes. So it is to be expected that a similar treatment of 3-D crystals would be much more complicated. An indication pointing to this is the fact that in 2-D crystals only 17 fundamentally different periodic patterns of motifs are possible, the 17 Plane Groups, while in 3-D crystals 230 such patterns are possible, the 230 Space Groups.
However, for those readers who might wish to know more details of the structure of three-dimensional crystals (and deepen their insight still more into that of two-dimensional crystals, generally, 2-D periodic patterns), he or she should study some relevant aspects of GROUP THEORY, which is the very (mathematical) theory concerning symmetry. On the Second Part of this website I have given a general introduction to that theory supplied with many notes on crystal symmetry (and also on symmetries as we find them in organisms). It is followed by a systematic symmetry theory for 3-D crystals making use of many group theoretic concepts and theorems. The reader will then gain insight into the fundamental 3-D crystal lattices, Point Groups and Space Groups (The latter are the Groups that describe the total symmetry -- point symmetries and translational symmetries -- of 3-D crystals).
The mentioned Second Part of the website is accessible by the LINK at the end of the present document.
The internal structure, describable by the Space Group + Chemical Composition, is itself directly caused by the relevant crystallization law, which is the dynamical law of the dynamical system that consists of the growing crystal in its growing environment. This dynamical law is metaphysically interpreted as the Essence of the crystals, i.e. the essence of any individual (single) crystal (that is) generated according to that particular dynamical law (Other crystal species are associated with different dynamical laws).
The pattern of growth rates in several directions (that is the growth rates of the possible crystal faces) determines the intrinsic shape of the crystal (as one of the features of the crystal). The growth rate of a possible face depends on its atomic aspect that it presents to the growing environment. This aspect itself is determined by the density of lattice nodes that are intersected by that face (See Figure 27) and the chemical composition of the crystal, especially which chemical units border on the growing environment.
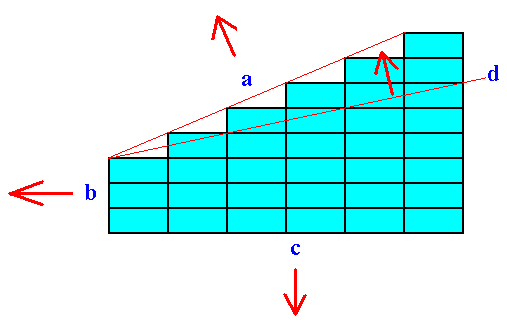
Figure 27. Besides the chemical composition (chemical aspect presented to the environment) the growth rate of a face is inversely proportional to the number of lattice nodes that are encountered by that face.
The figure shows a primitive rectangular point net (The argument to come also applies to a 3-D point lattice). The intersections of the lines making up the rectangular cells (meshes) are lattice nodes (These nodes represent the locations of chemical units).
Four possible faces are indicated by a, b, c and d. The arrows indicate their respective directions of growth (At the same time there is also a corresponding growth in the opposite directions of the arrows). Generally the slowest growing faces become the most prominent faces on the crystal. The fastest growing faces quickly grow themselves out of existence.
This Figure -- which concerns the growth rates of faces -- only pays attention to one feature of the atomic aspect (The atomic aspect determines the growth rate of a face), namely the density of nodes encountered by the crystal face in question (The other feature refers to the chemical composition of the crystal).
The slowest growing face (on the basis of the feature mentioned) is face b, because here the density of nodes (encountered by that face) is highest.
Next comes face c, and then a.
The fastest growing face is d.
So the faces b and c will become the most prominent faces. The other faces will eventually grow themselves out of existence.
Because the faces b and c are perpendicular to each other the faster growing face of these two, namely c, will not grow itself out of existence. It keeps on growing, and keeps on growing faster than b, so the crystal will finally adopt a rectangular shape with its longest dimension oriented vertically.
Besides all this also energy considerations should be part of the insight concerning (the generation of) crystals. We will discuss these later on in a special 'thermodynamic' Essay. And only then we can begin to understand and interpret any single crystal as the product of a certain dynamical system. And having a crystal understood this way we can assess the ontological nature of any single crystal, i.e. we can commit ourselves to a metaphysics of a large part of the inorganic world. Of course we have already done so in several previous Essays of this website, but there it was more or less cursory. Now we're going deep down into the matter (as is appropriate and to be expected in this Special Series of Essays).
With the present document (i.e. Part XX, about the internal structure od 2-D crystals) we have come to an end of the First Part of this website. And, as has been said, the Second Part (after having given a Retrospect of what was done on the First Part) will start with Group Theory, geared toward an understanding of three-dimensional crystals, and then finish our exposition on the latter, including their thermodynamics, twins etc.. It will be followed by an organic 'tectology', i.e. a study of the general structure of organisms, which prepares for an investigation into the basic symmetries as found in organisms (Promorphology).
If one wants to know more about a HOLISTIC approach with respect to the structure of Reality (with alternative interpretations about the generation of crystals and organisms, but also of other things), one can go to the Third Part of the website by clicking on the last LINK in the contents (left frame).
To continue, click HERE (to Second Part of Website)
back to homepage