
e-mail :

In the previous document we studied crystals having the (total) symmetry according to the Plane Group Pm. Two types of possible motifs with D1 symmetry were investigated as to the Promorph they would imply.
In the present document we will consider still other motifs that have D1 symmetry and that can therefore also constitute a Pm pattern. Also these different motifs, although not changing any symmetry, imply different Promorphs (i.e. different species of the Heterostaura allopola or half amphitect pyramids).
The following motif, having D1 symmetry, will be placed in a primitive rectangular lattice, resulting in a Pm pattern :

Figure 1. Newly chosen motif to constitute a Pm pattern.
An enlargement of this motif is shown in the next Figure.
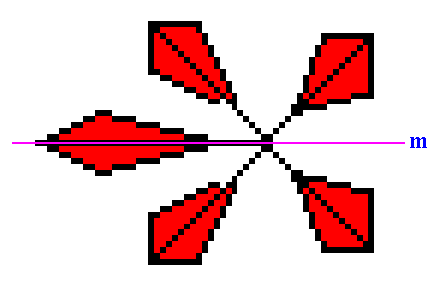
Figure 2. Magnification of the newly chosen motif as depicted in the previous Figure.
It has D1 symmetry. Its mirror line is indicated. The motif consists of five similar antimers, symmetrically arranged with respect to the mirror line. The Promorph of this motif clearly belongs to a 2-D analogue of the Pentamphipleura (Heterostaura allopola amphipleura).
A possible 2-D crystal having this structure, i.e. consisting of a periodic repetition of the above motif according to a primitive rectangular lattice, is given in the next Figure.
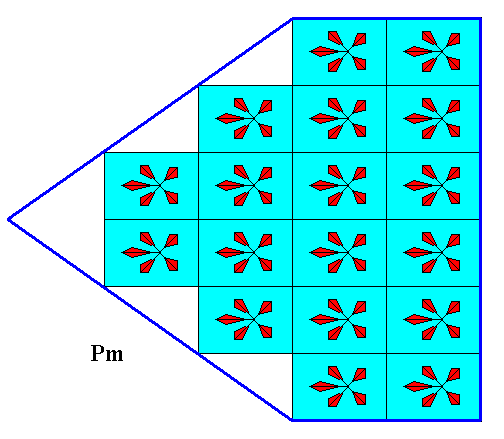
Figure 3. A possible 2-D crystal having the above described internal structure.
It consists of three Forms :
An alternative unit cell still contains five antimers of the motif (2 + 2 + 1/2 + 1/2) :
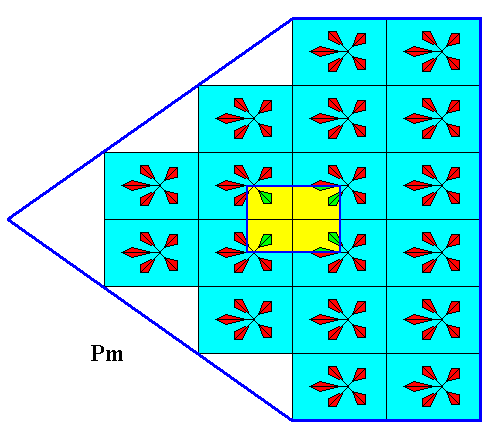
Figure 4. Alternative unit cell (mesh) also contains five antimers, i.e. it contains a motif consisting of parts that are equivalent to the five antimers of the original motif.
The five antimers of the crystal of Figure 3 are indicated in the next Figure.
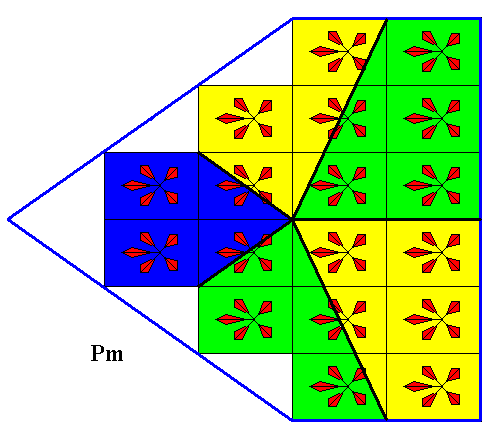
Figure 5. The five antimers of the 2-D crystal of Figure 3 are indicated. The boundaries separating these antimers are more or less arbitrary.
The structure, symmetry and content of the motif determines the lattice according to which it will be repeated under given 'thermodynamic conditions. It also determines the 'chemical' atomic aspect a face can present to the growing environment. All this in turn determines the pattern of relative growth rates and thus the Growth Rate Vector Rosette, and finally the Vector Rosette of Actual Growth which expresses the shape of the crystal. So in fact the translation-free (microscopic) motif determines the intrinsic Shape of the corresponding crystal under given thermodynamic conditions. And this means that the shape of that motif is somehow related to the intrinsic shape the corresponding crystal will adopt. That's why we have chosen from the set of geometrically possible crystals a crystal of which the shape is somehow comparable with the shape of the translation-free motif.
The D1 symmetry of all the Pm crystals determines the general Promorph of them to be that of a 2-D analogue of the Heterostaura allopola. However, to what species of the latter it belongs is not revealed by the Shape or Symmetry of the crystal, but is determined by the promorphology of the translation-free motif. And indeed the latter indicates that the Promorph of the crystal belongs to the 2-D analogue of the Pentamphipluera (Heterostaura allopola). The solid representing the 3-D Pentamphipleura is half a ten-fold amphitect pyramid as the next Figure shows.
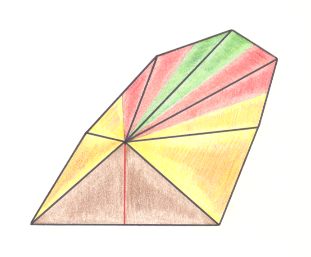
Figure 6. Oblique top view of the Stereometric Basic Form of the Pentamphipleura. It is half a ten-fold amphitect pyramid. The five antimers are indicated by colors. The brown plane facing towards the beholder is the bisection plane.
The antimers of a motif do not need -- in order for them to be true antimers -- to be equal, or exactly symmetric with respect to each other, as we have seen in the previous document. So our mirror symmetric motif can in other crystals (differeing slightly in 'chemical composition') be a motif where this mirror symmetry is lightly disturbed. Even then we will expect a crystal of a similar or equal shape as the one with the fully mirror symetric motif. And, as we saw, we can describe the point symmetry of this slightly asymmetric motif, and also the symmetry of the periodic pattern that can be obtained from such a motif, by the corresponding antisymmetry groups. See next Figure.
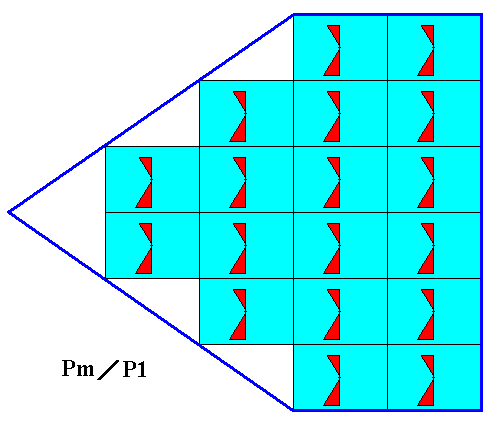
Figure 7. A two-dimensional crystal of which the classical symmetry of the internal structure is according to the Plane Group P1 , but of which the antisymmetry is according to the antisymmetry group Pm / P1 . In the latter interpretation the mirror reflection m is replaced by the antisymmetry transformation e1m , where the antiidentity transformation is the permutation (Large Small) (cycle notation). This permutation should mean that a large triangle must become small, and a small triangle must become large. The antisymmetry transformation e1m then reads : reflect in m and change the size of the triangle according to the mentioned permutation.
The two antimers of the above crystal are indicated in the next Figure.
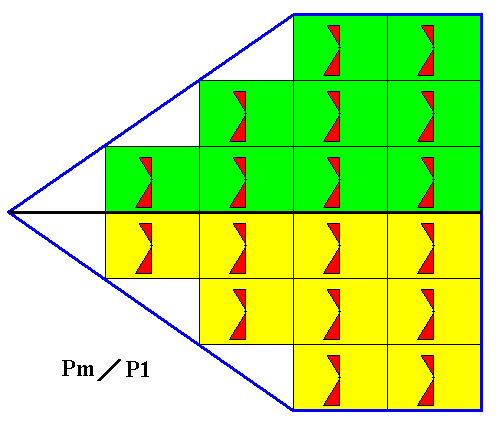
Figure 8. The two antimers of a two-dimensional crystal (as given in Figure 7) having P1 classicla symmetry, but Pm / /P1 antisymmetry, are indicated.
The Plane Group Pg
The next Figure gives a 2-D periodic pattern according to the Plane group Pg.
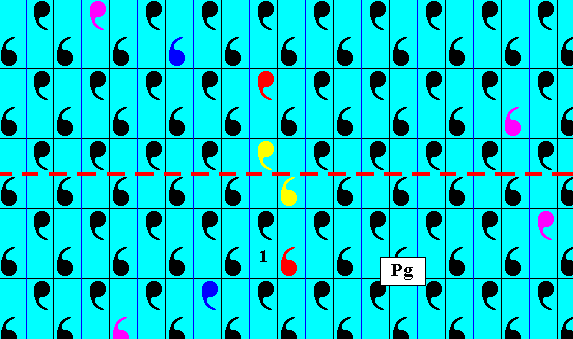
Figure 9. A pattern representing the Plane Group Pg .
The rectangular areas represent group elements (one such area is indicated as representing the identity element 1 ). The unit cell (unit mesh) and their equivalents consist of two such areas. A glide line (red dashed line) is indicated, and the colored motifs illustrate the action of this glide line (A glide line represents the following symmetry transformation : Reflect in the (glide) line and then translate half a translation distance along the glide line).
The next Figure depicts the same Pg pattern, but now the lines delineating the areas representing group elements deleted, and the above given coloration of the motifs undone.
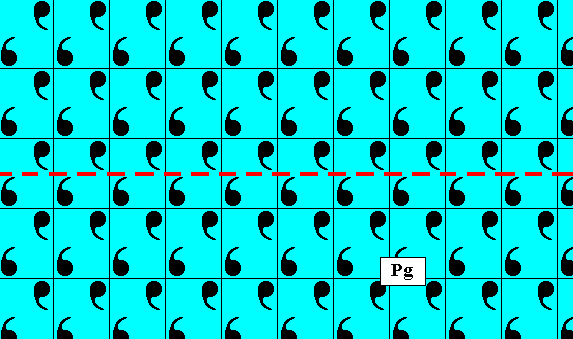
Figure 10. The Pg pattern of the above Figure. Each mesh contains a motif consisting of two commas related to each other by a glide reflection. A glide line is indicated (red dashed line).
The point symmetry of any Pg pattern is m (isomorphic to the group D1). This is so because when we eliminate all translations (in order to obtain the translation-free residue of the Plane Group, which is the Point Group), we also eliminate the translational component in all glide reflections. And because a glide reflection is a combination of a reflection and a translation, the reflection remains.
And it also holds for all crystals having a symmetry of their internal structure according to the Plane Group Cm, because also here the point symmetry is that of D1 (crystallographically denoted by m)
The Plane Group P2mm
The next Figure gives a periodic pattern according to the Plane Group P2mm.

Figure 11. A two-dimensional periodic pattern according to the Plane Group P2mm . The yellow and green areas represent group elements (they do not represent symmetry features). A unit mesh is indicated (blue).
The next Figure gives this same pattern, without indicating areas representing group elements.
Figure 12. The 2-D periodic pattern of Figure 11. The lattice underlying this pattern is a primitive rectangular net. Each mesh is provided with a motif consisting of four commas. The symmetry of the motif is according to the group D2 . The motif clearly has four antimers, not radially but bilaterally arranged.
There are two alternative ways to conceive of the motif (s.str.). One as the content of a mesh, the other as that content that is associated with a lattice point, i.e. the surroundings of a lattice point, where these surroundings occupy precisely the same space as a mesh does (only then they do not overlap or leave gaps, and are as such regularly repeated) :
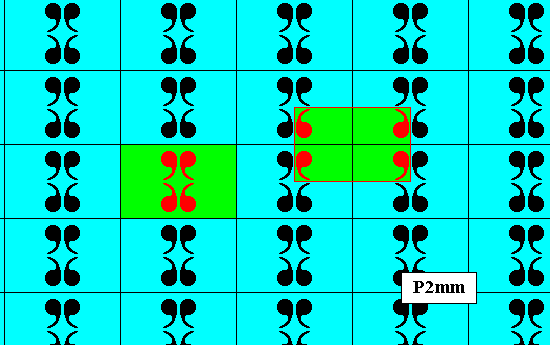
Figure 13. Two alternative ways to see the motifs of the P2mm pattern of the previous Figures. In both cases the motif has D2 symmetry, and is such that the directional axes (which are those promorphological axes -- expressing the polarity or non-polarity of the motif -- that are perpendicular to each other) are interradial, which means that they lie between the antimers of the motif.

Figure 14. The D2 motif of the above P2mm pattern has its directional axes in interradial positions. The commas represent antimers, and these in turn represent the radii of the motif.
From Figure 14 it is clear that the Promorph of this motif is a 2-D analogue of the Tetraphragma interradialia (Heterostaura autopola orthostaura). See for this our Promorphological System of Basic Forms (Second Part of Website). To see the document on the Autopola oxystaura and Autopola orthostaura (where under te latter reside the Tetraphragma interradialia) in a separate window (which, after consulting, must be closed in order to be back again at the present document), click HERE.
Figure 15. Slightly oblique top view of a rectangular pyramid. In case of there being four antimers it is the basic form of the Tetraphragma interradialia, or, (it could be interpreted as just) a modification of the Tetraphragma.
The directional planes of the Tetraphragma interradialia are interradial. The other cross planes (resp. cross axes) are radial but do not meet at right angles.
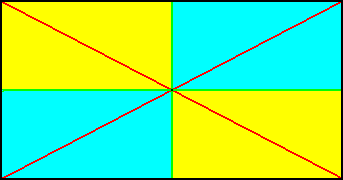
Figure 16. Equatorial plane (or base for that matter) of a rectangular pyramid with four antimers (indicated by coloration). The radial cross axes are indicated with red, the interradial cross axes (which here are at the same time the directional axes) are indicated with green.
So in virtue of the promorphology of the translation-free motif of the pattern of Figure 12, all 2-D crystals having this structure (i.e. having an internal structure with plane group P2mm, and possessing the motifs as given) have a Promorph belonging to the 2-D analogue of the Tetraphragma interradialia (Heterostaura autopola orthostaura).
The next Figure gives a possible crystal having the above structure.
Figure 17. A possible 2-D crystal having the structure as depicted in Figure 12. It consists of two Forms :
The point symmetry (i.e. the symmetry without translations) of this crystal is elucidated in the next Figure.
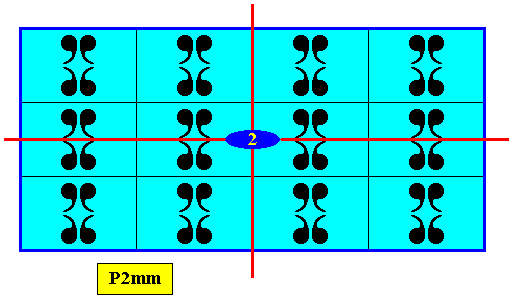
Figure 18. Point symmetry -- D2 -- of the 2-D crystal of the previous Figure. There are two mirror lines perpendicular to each other. In the point of intersection of these mirror lines there is a 2-fold rotation axis (perpendicular to the plane of the drawing).
Although other shapes of possible crystals having this particular structure are in principle possible, we assume that the structure of the translation-free motif has much influence on the shape adopted by the crystal, because, as has been said, the structure of the motif determines the atomic aspects presented to the environment by possible faces, that in turn determine the pattern of relative growth rates, and thus finally determine the intrinsic shape of the crystal.
On the basis of the motif as present in the above crystal, the latter must have four antimers :
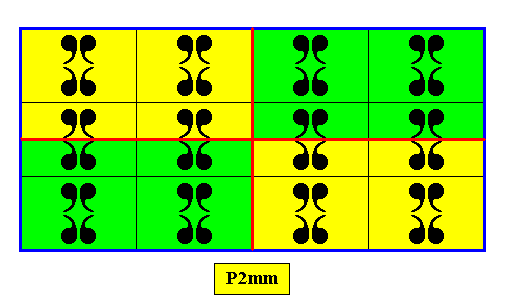
Figure 19. The four antimers of the 2-D crystal of Figure 17.
The two directional (directive) axes are posited interradially. The Promorph of the crystal therefore belongs to the 2-D analogue of the Tetraphragma interradialia (Heterostaura autopola orthostaura).
The point symmetry of crystals with Plane Group P2mm is a symmetry according to the group D2 (which is crystallographically denoted as 2mm). This point symmetry all by itself determines the general Promorph, viz. that of the Heterostaura autopola (amphitect pyramids) [themselves belonging to the Stauraxonia heteropola (single pyramids)].
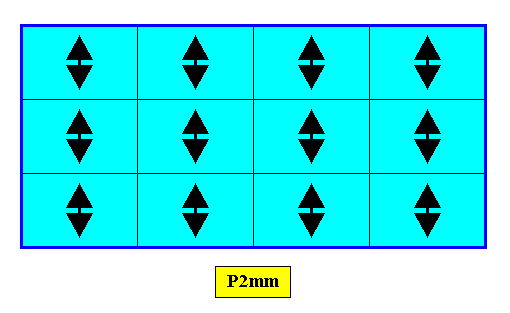
Figure 20. A possible crystal with (the symmetry of its internal structure according to the) Plane Group P2mm (as in Figure 12), but with different motifs.
It is however more likely that the shape of the crystal relates to the shape of the translation-free motif. This is expressed in the next Figure.
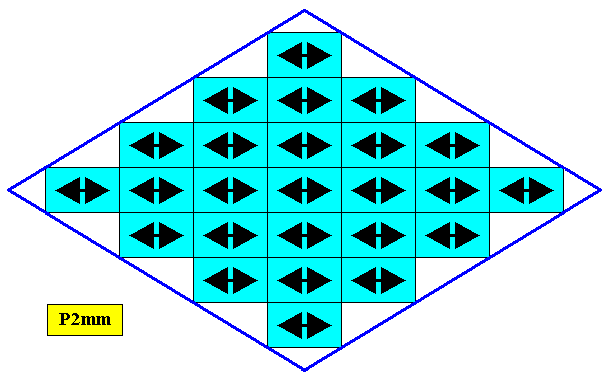
Figure 21. A possible crystal with ( the symmetry of its internal structure according to the) Plane Group P2mm (as in Figure 12), having motifs as present in the previous Figure. While the symmetry of these motifs is still according to the symmetry group D2 , such a motif consists of only two antimers (instead of four). The Promorph of such a motif is therefore belonging to the 2-D analogue of the Orthostaura diphragma (Heterostaura autopola).
The crystal consists of one Form only, viz. the four oblique 'faces' : When one such oblique face is subjected to the symmetry of this crystal, which is according to the group D2 , three more such faces are automatically generated by the symmetry elements (two perpendicular mirror lines and a 2-fold rotation axis going through their intersection), resulting in a closed Form consisting of four faces.
The two antimers of the above crystal are indicated in the next Figure.
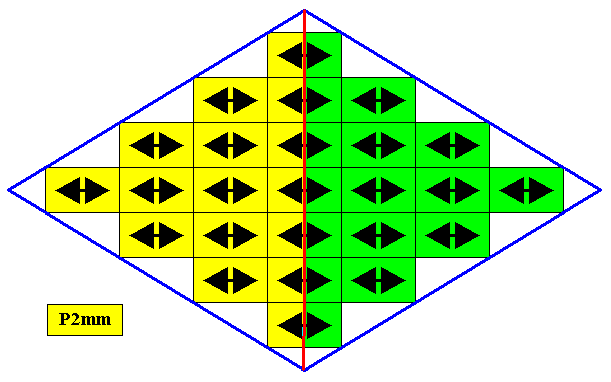
Figure 22. The two antimers of the crystal of the previous Figure.
The Promorph is of the crystal is then that of the 2-D analogue of the Orthostaura diphragma (Heterostaura autopola).
Itis perhaps convenient to add some explanation as to the difference between the Orthostaura diphragma and the Orthostaura tetraphragma :
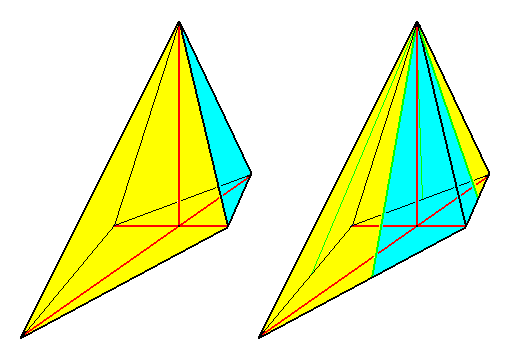
Figure 23. Perspectivic view of a Rhombic pyramid.
Left image : Rhombic pyramid with t w o antimers, representing the basic form of the D i p h r a g m a.
Right image : Rhombic Pyramid with four antimers (basic form of the Tetraphragma).
The stereometric basic form of the Diphragma is, as of the Tetraphragma, the Rhombic Pyramid. So in itself there is no difference between the two forms. As soon, however, one compares them with kindred forms that have other basic forms, one sees that in the Diphragma the body is composed of just two congruent antimers, while in the Tetraphragma it is composed of four antimers. While further in the Tetraphragma two pairs of cross planes are present (two radial and two interradial), there is only o n e radial and o n e interradial cross plane in the Diphragma, of which the radial cross plane coincides with the lateral directional plane, the interradial with the sagittal directional plane. See next Figure.
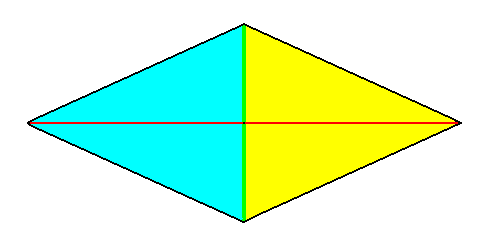
Figure 24. Base (or a plane parallel to it and containing the mid-point of the main axis) of a four-fold amphitect pyramid as the basic form of the Autopola orthostaura diphragma. This configuration represents organismic forms with only t w o antimers. These a n t i m e r s are indicated by colors. There is only one radial cross axis (red) and one interradial cross axis (green). These two axes coincide with the directional axes. The axis, indicated with green is indeed interradial because it lies between antimers.
The two antimers must of course be congruent, because the dorsal side differs as little from the ventral side as the right side from the left.
The next Figure gives a possible 2-D crystal also having an internal symmetry according to the Plane Group P2mm, but with a different translation-free motif. This motif, however, has the same point symmetry -- D2 -- as the motif considered above.
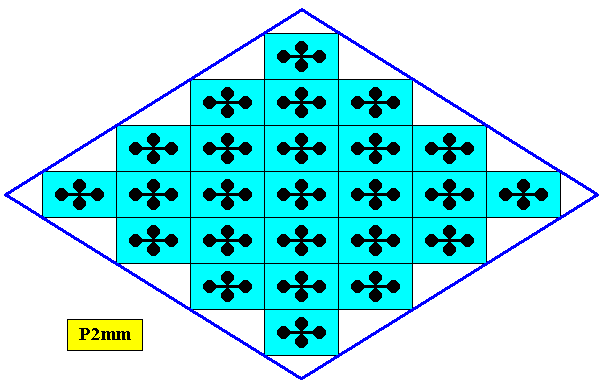
Figure 25. A possible 2-D crystal, still having internal P2mm symmetry, but with a different translation-free motif. Although this motif still has a point symmetry according to the group D2 , it has four antimers, like the motif in Figure 12, but they are differently arranged. The Promorph of this motif is belonging to the 2-D analogue of the Tetraphragma radialia (Heterostaura autopola orthostaura). See next Figure.
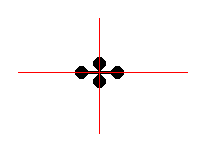
Figure 26. The translation-free motif of the crystal of the previous Figure has four antimers, arranged in such a way that the directive axes go through these antimers, meaning that these axes are radial. We could think of the motif as consisting of four equally sized, but qualitatively different atoms or atomic complexes.
The four antimers of the above crystal are indicated in the next Figure.
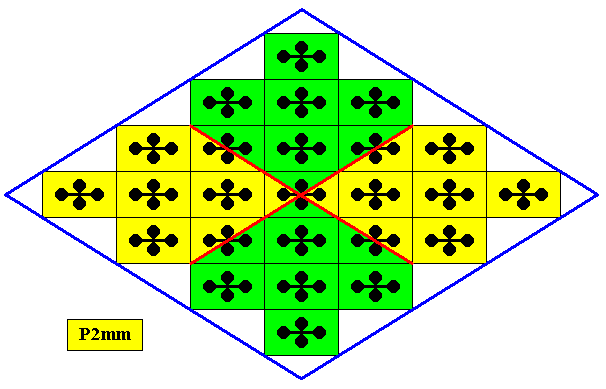
Figure 27. The four antimers of the above crystal are indicated.
The Promorph of the crystal therefore belongs to the 2-D analogue of the Tetraphragma radialia (Heterostaura autopola orthostaura).
The next Figures elucidate the Tetraphragma radialia.
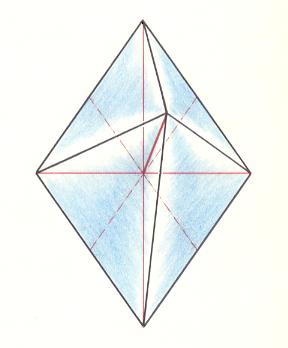
Figure 28. Slightly oblique top view of a Rhombic Pyramid as the basic form of the Tetraphragma radialia.
The main axis, the directional axes and the interradial cross axes are indicated.
These Tetraphragma radialia can be best understood by comparing them to related promorphs. First to promorphs from which they can be derived, viz. the Homostaura tetractinota (regular single 4-fold pyramids), and then to promorphs which can be derived from them (i.e. from the Tetraphragma radialia), viz. the Eutetrapleura radialia (bi-isosceles pyramids, Heterostaura allopola zygopleura). For comparing these promorphs it is sufficient to consider their respective equatorial planes (planes parallel to the base of the pyramid and passing through the mid-point of its main axis) or, equivalently, to consider their bases (and these equatorial or basal planes are at the same time their 2-D analogues) :
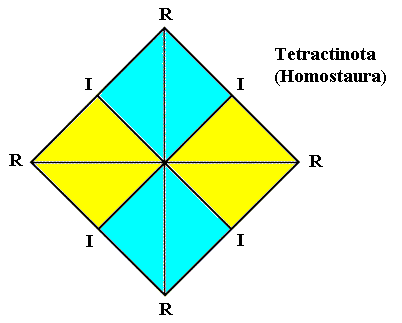
Figure 29. Equatorial plane (or base for that matter) of a regular 4-fold pyramid. This pyramid is the basic form of the Homostaura isopola tetractinota. Radial cross axes are indicated as R, interradial cross axes as I. The four antimers are indicated by coloration.
From this form can be derived the Rhombic Pyramid of the Autopola tetraphragma radialia by differentiating between the two directional axes (See next Figure).
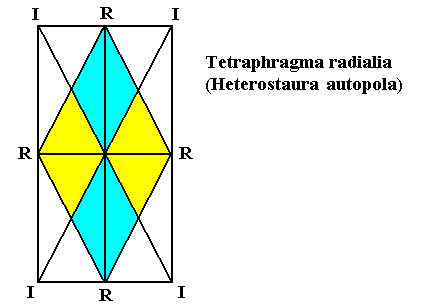
Figure 30. (colored image within the rectangle) Equatorial plane (or base for that matter) of an amphitect 4-fold pyramid (with four antimers). This pyramid is the basic form of the Autopola tetraphragma radialia (Heterostaura). Radial cross axes are indicated as R, interradial cross axes as I. The four antimers are indicated by coloration.
From this form can be derived the basic form of the Eutetrapleura radialia by making one of the directional axes heteropolar (See next Figure).
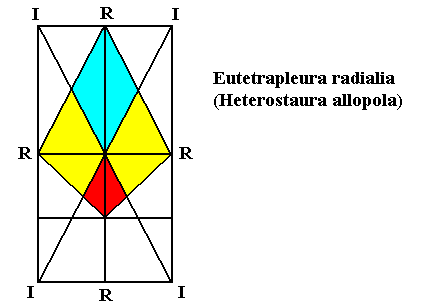
Figure 31. Equatorial plane (or base for that matter) of an ideally halved (i.e. without thereby loosing antimers) 4-fold amphitect pyramid (with four antimers). This ideally halved pyramid is the basic form of the Allopola eutetrapleura radialia (Heterostaura).
Radial cross axes are indicated as R, interradial cross axes as I. The four antimers are indicated by coloration.
The next Figure gives a possible crystal, again with an internal symmetry according to the Plane group P2mm, but with a different translation-free motif, although still having D2 symmetry.
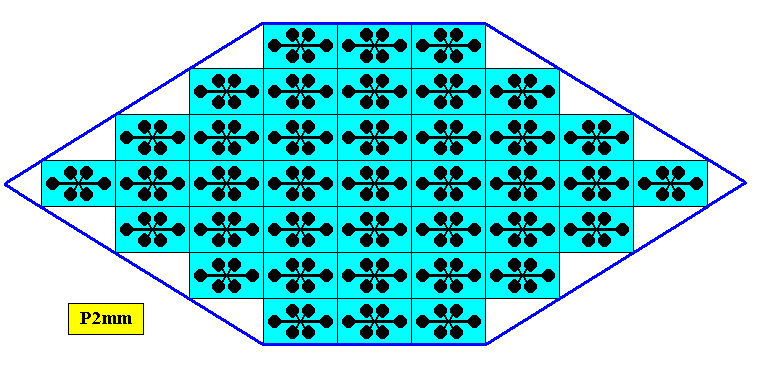
Figure 32. A possible crystal with (the symmetry of its internal structure according to the) Plane Group P2mm (as in Figure 12), but with different motifs. Such a (different) motif still has D2 symmetry but possesses six antimers, arranged in such a way that the promorph of the motif belongs to the 2-D analogue of the Oxystaura hexaphragma (Heterostaura autopola).
The crystal consists of two Forms :
The next Figure indicates the six antimers of the crystal of Figure 32.
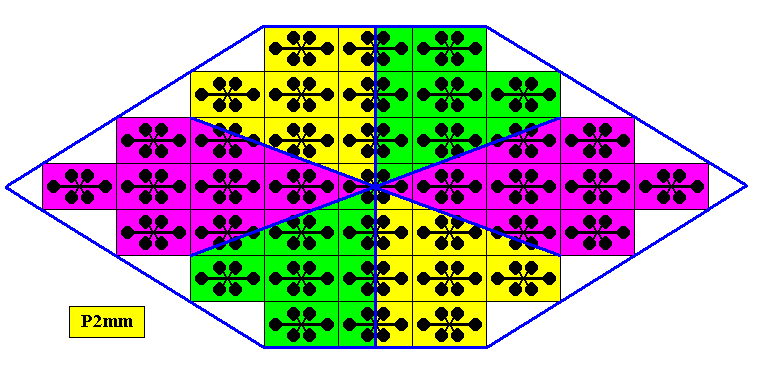
Figure 33. The six antimers of the crystal of Figure 32 are indicated.
The Promorph of the crystal of Figure 32 is consequently belonging to a 2-D analogue of the Oxystaura hexaphragma (Heterostaura autopola).
The next Figures elucidate the Oxystaura hexaphragma.
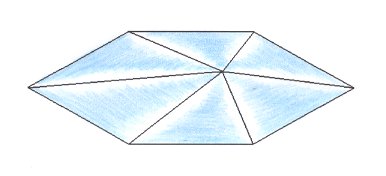
Figure 34. Slightly oblique top view of a six-fold amphitect pyramid as the basic form of the Oxystaura hexaphragma.
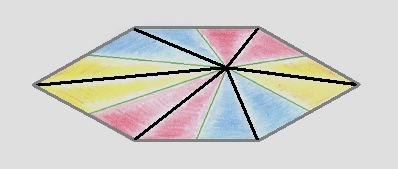
Figure 35. Slightly oblique top view of a six-fold amphitect pyramid as the basic form of the Oxystaura hexaphragma. The six a n t i m e r s are indicated by colors.
In the previous document we discussed the Plane Group Pm. The motifs compatible to this Plane Group have D1 symmetry, and can consist of two, four or more (generally 2n) antimers. All the crystals having a symmetry of their internal structure according to the Plane Group Pm, and thus having D1 point symmetry, promorphologically belong to the 2-D analogue of the Heterostaura allopola, which are, however, still representing a general promorph (the 2-D Heterostaura allopola are half amphitect polygons, while the 3-D Heterostaura allopola are half amphitect pyramids). Only the number and arrangement of the antimers of the translation-free motif will determine the promorph still further. When there are four antimers present in such a motif we established that the following 2-D crystal, also having four antimers, was possible :
Figure 36. A two-dimensional crystal (consisting of three Forms) having Pm plane group symmetry and D1 point group symmetry. The translation-free motif consists of four similar antimers, determining the Promorph of the crystal to belong to a 2-D analogue of the Eutetrapleura interradialia (as a species of the Heterostaura allopola zygopleura).
But the symmetry of the crystal of Figure 36 can also be interpreted as the result of a desymmetrization of the Plane Group P2mm (and of the Point Group D2) by antisymmetry :
If the motif is found to represent D2 symmetry, and has four equal antimers arranged in such a way as to result in a promorph belonging to the 2-D analogue of the Tetraphragma interradialia (Heterostaura autopola), then the right half must be relflected in the line a (see next Figure) going through the two antimers residing in this right half, and at the same time be reduced in size. If, on the other hand, the motif is found to be in the latter state, it must reverse to the first state.
In short we can describe e1 as the permutation
Graphically this looks as follows :
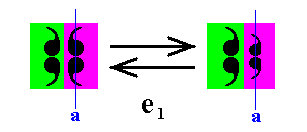
Figure 37. Illustration of the action of the antiidentity transformation e1 . It acts on the right half of the motif.
The full antisymmetry transformation is then e1m , which must (in order to be a genuine antisymmetry transformation) be equal to me1 , which reads :
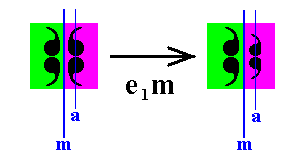
Figure 38. The action of the antisymmetry transformation e1m . If this transformation is performed two times, then the net effect is nil : e1me1m = 1.
So if we replace, in the Plane Group P2mm, the vertical reflection m by the above given antisymmetry transformation e1m , then we end up with the antisymmetry group P2mm / Pm, which is isomorphic to P2mm.
This concludes our discussion of the Plane Group P2mm.
In the next document we will continue our investigation into the Shape, Symmetry and Promorph of 2-dimensional crystals.
To continue click HERE for further study of the Theory of Layers, Part XXXIV.
e-mail : 